
При внецентренном растяжении (сжатии) бруса (стержня) внешняя сила не совпадает с осью стержня, а смещена относительно продольной его оси, оставаясь ей параллельной. Расчет стержней при внецентренном нагружении можно провести нескольким и методами:
1. Точный метод - расчет стержня с учетом положения нейтральной линии;
2. Упрощенный метод - расчет стержня бет учета положения нейтральной линии
3. Метод конечных элементов (МКЭ).
Ниже приведены результаты расчета тремя перечисленными методами применительно к стержню, нагруженному эксцентрично приложенной силой F =40кН. и имеющему следующие размеры прямоугольного поперечного сечения: h =20мм, h = 60мм и l= 200мм (рис. 1).

Уточненный метод . Вначале создается эквивалентная схема нагружения стержня, для чего сила F переносится параллельно самой себе на ось стержня. Соот¬ветственно, стержень должен быть нагружен моментом М = Fе (рис. 1б). Напряжения на расстоянии у от оси x (рис. 1в) определяются с помощью принципа независимости действия внешних силовых факторов (F и М ).
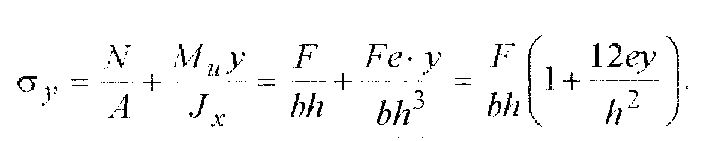
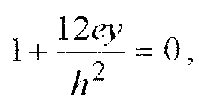

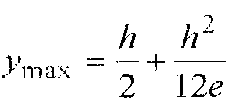
Значение наибольших напряжений для точного метода расчет стержня при вне внецентренном нагружении будет равно:
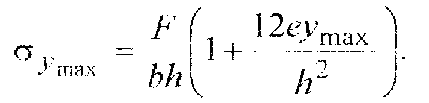
Упрощенный метод. В этом случае суммируются напряжения от действия силы F и максимальные напряжения от действия момента М :
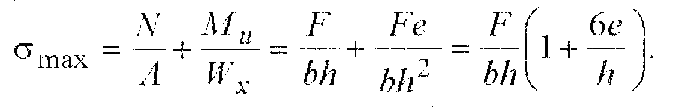
Метод конечных элементов. Конечно-элементный анализ эксцентрично нагруженного стержня осуществлялся в системе АРМ WinMachine компании АПМ (НЦП «Автоматизированное проектирование машин», г. Королев. Московская обл.).
Стержень разбивался на 500 тетраэдров, соединенных между собой. Один горец стержня всеми узлами жестко закреплялся, а к свободному концу прикладывалась эксцентричная сила F . Напряжения определялись по цветовой гамме.
Значения эксцентриситета е для расчета напряжений по формулам (5), (6) и вы¬бора напряжений но цветовой гамме принимались следующими: е = 30мм, е-45мм. е = 60мм и е = 75.мм.
В результате расчетов получил данные, по которым построил графики на (рис.2).

Анализ полученных результатов показывает, что приближенный метод занижает напряжения на 15-20%, что допустимо только при больших значениях запаса прочности. Значительное занижение напряжений (20-30%) при применении метода конечных элементов может быть объяснено недостаточным количеством конечных элементов, поскольку программа высвечивает среднее значение напряжений в пределах элемента. Увеличение количества элементов требует применения компьютеров большой мощности и более специализированных программ (например, ANSYS). Применение метода MKT) целесообразно для анализа напряженного состояния объектов сложной конфигурации, для которых большое значение имеет не абсолютное значение напряжений, а их распределение.