ОПРЕДЕЛЕНИЕ СОПРОТИВЛЕНИЯ ДЕФОРМАЦИИ ХРОМОНИКЕЛЕВЫХ СТАЛЕЙ В УСЛОВИЯХ ШЛИФОВАНИЯ С ПОМОЩЬЮ ТЕРМОМЕХАНИЧЕСКИХ КОЭФФИЦИЕНТОВ

Полтавец В. В.
(ДонНТУ, г. Донецк, Украина)

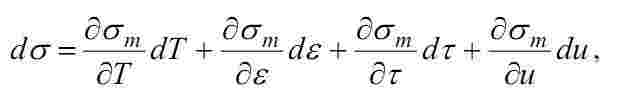
Источник: http://www.nbuv.gov.ua/portal/natural/Npdntu/Mim/2008/rozdil1/poltavets.pdf

       Согласно теории А. Надаи, сопротивление металлов деформации описывается уравнением:

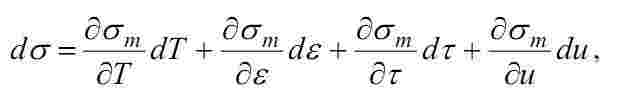
Рисунок 1.


       Слагаемые уравнения (1) учитывают влияние на сопротивление деформации температуры, наклепа (относительной деформации), разупрочнения во времени, изменения напряжений в зависимости от скорости деформации с учетом вязкости металла.
       До настоящего времени закономерности, необходимые для решения уравнения (1), недостаточно изучены. Поэтому на практике для определения используют экспериментальные данные в виде конкретных дискретных значений для определенных условий деформирования и марок стали или зависимости, аппроксимирующие экспериментальные данные [1].

Исследования по определению сопротивления деформации сталей и сплавов проводят с применением специальных машин, из которых наиболее распространены пластометры различного типа [2, 3]. При испытаниях на них можно воспроизвести заданный закон деформации во времени, менять степень и скорость деформации в исследуемом интервале этих параметров, производить испытания при высоких температурах, измерять усилия и величины деформации в функции времени. Тем не менее, ско- рости деформации, характерные для процесса механической обработки (при лезвийной обработке в зоне резания скорость деформации достигает 106 с–1, а при шлифовании – 107 с–1) на пластометрах недостижимы.
По характеру наиболее значимых процессов, происходящих в металле, к резанию ближе всего холодная деформация при обработке давлением. Для этого вида обработки разработан ряд методов определения сопротивления металла деформации по данным пластометрических испытаний, из числа которых наиболее удобными при применении ЭВМ являются методы, основанные на использовании термомеханических коэффициентов [1, 4, 5]. Применение термомеханических коэффициентов дает возможность расчленить многозначную функциональную зависимость на ряд частных зависимостей между тремя переменными kT(T),ku(u).

      Целью данной работы является исследование возможности распространения ме- тода термомеханических коэффициентов на область изменения температурноскоростных факторов при обработке резанием на примере труднообрабатываемых средне- и высоколегированных хромоникелевых сталей.

Основное содержание работы

      Сущность метода термомеханических коэффициентов состоит в том, что сопро- тивление деформации определяют при средних значениях термомеханических параметров в области динамических испытаний, а затем при помощи термомеханических коэффициентов kt, ku распространяют на всю исследуемую область динамических испытаний. Этот метод основан на усредненном значении степенного коэффициента k, во всей области динамических испытаний. Показано, что, несмотря на то, что k, строго говоря, не является постоянным при различных значениях температуры и скорости деформации, его отклонения от номинальных значений небольшие [4]. .
       Расчетное значение сопротивления деформации в зависимости от различных значений температуры, скорости и степени деформации В.И. Зюзиным предложено определять по следующей зависимости [4]
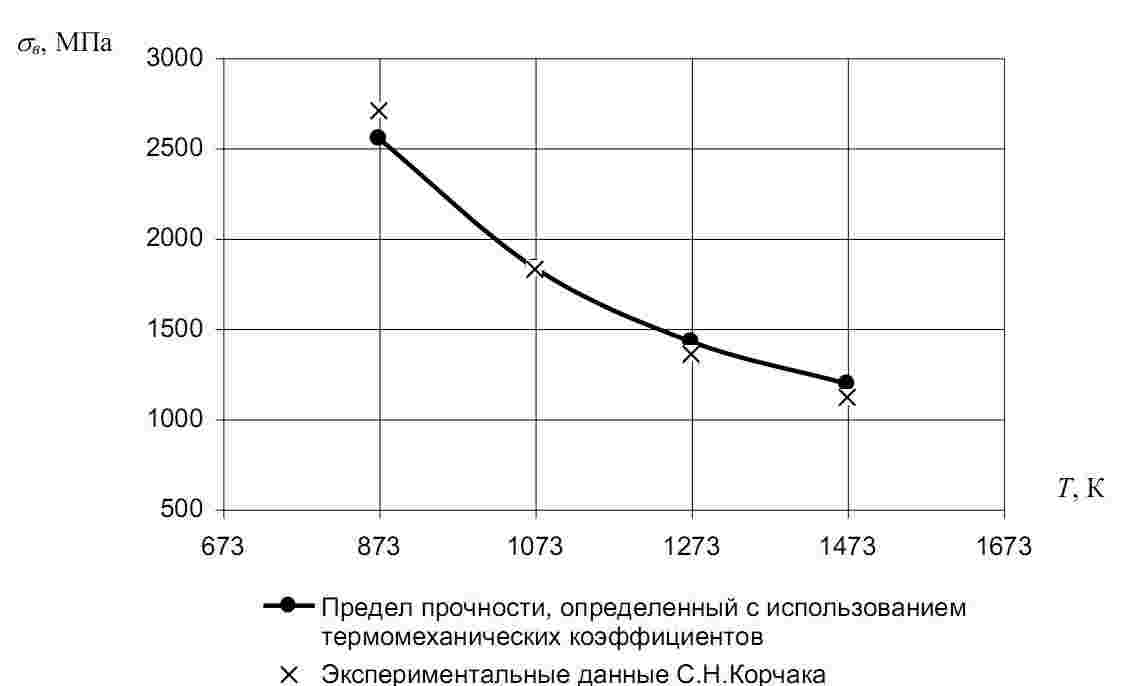
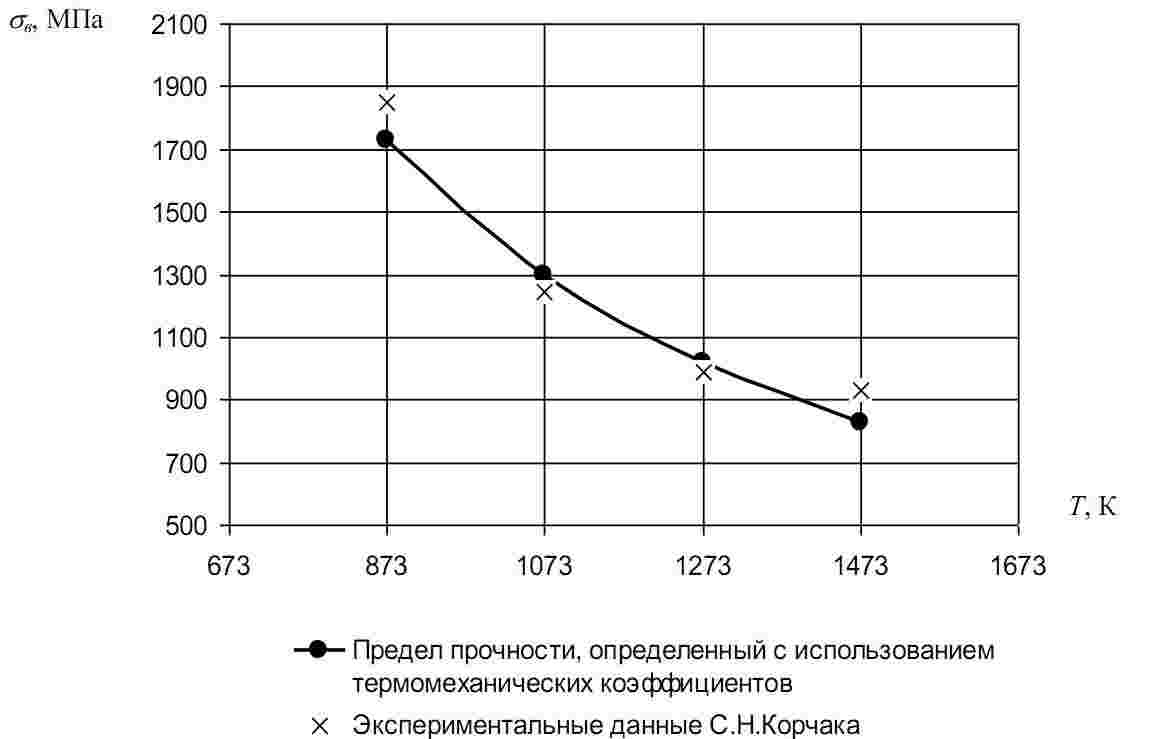
      Определим погрешность расчета предела прочности по зависимости (6) по срав- нению с экспериментальными данными С.Н. Корчака (рис. 1).

Рисунок 2.


      Как видно из рис. 1, в температурном диапазоне 600-1200C применение метода термомеханических коэффициентов с учетом принятой поправки позволяет определять значения механических характеристик сталей 12Х18Н9Т и Х18Н10Т в условиях деформирования при шлифовании, которые весьма близки к экспериментальным данным С.Н. Корчака. Максимальная погрешность определения предела прочности при этом не превышает 7%.
      Определим погрешность расчета предела прочности по зависимости (8) по сравнению с экспериментальными данными С.Н. Корчака (рис. 2).
Рисунок 2.


      Как и в предыдущем случае, в соответствии с рис. 2 в температурном диапазоне 600-1200C применение метода термомеханических коэффициентов с учетом принятой поправки позволяет определять значения механических характеристик сталей 12ХН3А и 12Х2Н4А в условиях деформирования при шлифовании. Максимальная погрешность определения предела прочности по сравнению с экспериментальными данными С.Н. Корчака составляет 11%.

Выводы
      1. Показана возможность определения сопротивления деформации при шлифовании с использованием термомеханических коэффициентов пут?м введения поправок, учитывающих скорость деформации при абразивной обработке.
      2. Погрешность определения предела прочности при использовании метода тер- момеханических коэффициентов не превышает 10-12 % по сравнению с эксперимен- тальными данными, полученными для температурно-скоростных условий шлифования.

Список использованных источников
  1. Коновалов Ю.К., Остапенко А.Л., Пономарев В.И. Расч?т па- раметров листовой прокатки: Справочник. – М.:. Металлургия, 1986. – 430 с.
  2. Третьяков А.В., Зюзин В.И. Механические свойства металлов и сплавов при обработке давле- нием. – М.:. Металлургия, 1973. – 224 с.
  3. Хензель А, Шпиттель Т. Расч?т энергосило- вых параметров в процессах обработки металлов давлением. – М.: Металлургия, 1982. – 360 с.
  4. Зюзин В.И. – Труды ВНИИМетмаш. Сб. № 8. – М.: ВНИИМетмаш, 1963. – С.
  5. Зюзин В.И., Бровман М.Я., Мельников А.Ф. Сопротивление деформации ста- лей при горячей прокатке. – М.:. Металлургия, 1964. – 270 с.

Библиотека