Библиотека

Выбор минимального радиуса центрового профиля кулачка с применением вычислительной техники

Пархоменко В.Г. Макаренко Д.Е. (ДонНТУ, г. Донецк, Украина),

Кучер В.С. (ДИАТ, г. Донецк, Украина)

 

Важнейшей задачей динамического синтеза кулачкового механизма является выбор минимального радиуса центрового профиля кулачка – r₀. Он осуществляется из условия ограничения угла давления α ≤ α_max. Как видно из рис. 1, сила P, действующая на толкатель 2 со стороны кулачка 1, раскладывается на 2 составляющие: P₁ = P·cos(α) и P₂ = P·cos(γ), где α – это угол давления, γ – угол передачи движения. Углом давления называется угол между вектором скорости конца толкателя и нормалью, проведенной к профилю кулачка через точку контакта. Углом передачи движения является не тупой угол между вектором скорости конца толкателя и касательной к профилю кулачка, т.е. дополняющий угол альфа до 90° (рис. 1). Составляющая P₁ совпадает по направлению с вектором скорости конца толкателя, т.е. обеспечивает его движение. Поэтому угол давления делают как можно меньшим. P₂ – «вредная» составляющая, которая может при достаточно больших значениях α (или малых γ) привести к заклиниванию механизма. Поэтому на практике значение α_max или γ_min = 90° – α_max назначают для конкретных условий по обобщенным теоретическим и практическим опытным данным.

Рисунок 1 – Схема кулачкового механизма с вращающимся толкателем

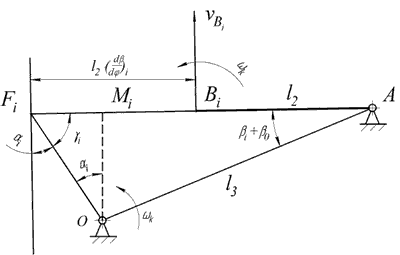
Рисунок 2 – Схема для определения угла давления

Как следует из рис. 2, Угол давления в проивольном положении кулачкового механизма с вращающимся толкателем определяется следующим образом:

.
Отрезки AF_i и AM_i соответственно равны:

.
Следовательно,
,
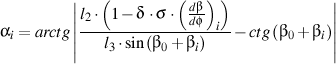где σ,δ – параметры сборки, определяющие конструктивные особенности заданной схемы:
δ = +1, кулачок вращается по ходу часовой стрелки;
δ = -1, кулачок вращается против хода часовой стрелки;
σ = +1, толкатель смещен вправо от оси вращения кулачка;
σ = -1, толкатель смещен влево от оси вращения кулачка.

Алгоритм работы программы определения минимального радиуса показан на рис. 5.
Работа программы проходит в следующей последовательности:
Пользователь выбирает закон изменения аналога ускорения и вводит исходные данные. При этом нажатием на кнопку «вычислить мин. значение» предлагается вычислить минимальное значение длины стойки l₃. В случае если значение l₃ будет введено меньше минимального, программа автоматически исправит его на минимальное. Алгоритм работы подпрограммы выбора минимального значения l₃ приведен на рис. 3.

Рисунок 3 – алгоритм работы подпрограммы выбора

После ввода исходных данных необходимо нажать на кнопку Вычисление r₀, после чего начнется выполнение основной программы.
Вычисление минимального начального значения r₀  производится по условию:
,
Следовательно,
.
Если условие не выполнится, r₀ будет увеличено на 1 мм и цикл повторится.
Далее определяется величина угла бета по формуле:
.
Значение угла поворота кулачка изменяется в заданных пределах с определенным шагом и производится расчет параметров бета и  в соответствии с заданными законами их изменения. Для каждого текущего значения угла поворота кулачка находится соответствующее значение угла давления и осуществляется логическая проверка условия α ≤ α_max.
Если условие не выполняется, то значение r₀ изменяется:
.
Итерационный цикл расчета повторяется до тех пор, пока не выполнится условие α ≤ α_max. Значение r₀, при котором осуществляется последний цикл расчета, выводится на экран.

Рисунок 4 – окно программы

Рисунок 5 – Алгоритм программы.

Список литературы

1. В.С.Кучер, Э.Л.Гордиенко. Методические указания по аналитическому синтезу кулачковых механизмов в курсовом проектировании. Донецк, ДПИ ,1992 – 43 с.

Библиотека