Сборочные процессы являются сложными технологическими про-цессами. Сборочные операции являются различными по времени их вы-полнения и сложности, поэтому для обеспечения выполнения заданного технологического процесса сборки довольно часто необходимо использование разветвляющихся сборочных систем (рис. 1). Разветвляющаяся сборочная система, основанная на системах непрерывного действия, состоит из одного входного и n количества выходных роторов. При функционировании таких систем возникает проблема определения взаимодействия позиций входного ротора с позициями последующих выходных роторов. На основании этого ставим цель работы: определение параметров маршрутизации движения промежуточных сборочных компонент или изделий для разветвляющегося выходного потока (маршрута).

   Разветвляющимся выходным маршрутом называется такой маршрут, который образуется после выхода промежуточных сборочных компонент с входного ротора и последовательной их передачи на позиции -го количества выходных роторов.

   Для достижения поставленной цели необходимо решить следующие задачи:

   1. Определить количество различных маршрутов движения промежу-точной сборочной компоненты или изделия;

   2. Определить параметры полного кинематического цикла движения промежуточной сборочной компоненты или изделия;

   3. Определить, в каком номере маршрута участвуют те или иные пози-ции входного и выходных автоматических технологических сборочных модулей.

   Количество различных маршрутов - это максимально возможное их количество без учета повторения.

   Полным кинематическим циклом движения маршрутов промежу-точной сборочной компоненты или изделия называется то количество маршрутов, которое образуется до момента повторения цикла функционирования входного ротора, рабочие позиции которого должны совпасть с рабочими позициями выходных роторов аналогично началу функционирования всей сборочной системы.

   Условно назовем ротор, который выполняет i-ую операцию технологического процесса, входным ротором, а роторы, выполняющие (i+1) -ую операцию - выходными роторами.

   Рассмотрим автоматическую технологическую сборочную систему, состоящую из множества автоматических технологических сборочных модулей первого класса P = {P1, P2},

   где P1 - входной сборочный ротор, состоящий из V1 количества позиций, {P1} = {1, 2, ..., V1}; P2 - множество, описывающее общее количество выходных роторов, P2 = {P21, P22, ..., }, где, в свою очередь, P2i = {1, 2, ..., V2i} (рис.1), выполняющую комплекс операций заданного технологического процесса.

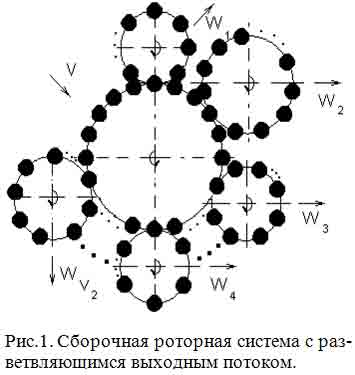
   Маршрутом промежуточной сборочной компоненты или изделия называется определенная совокупность позиций входного и i-го выходного роторов, участвующих в технологическом процессе сборки и транспортирования (если таковое имеет место) от позиции загрузки промежуточной сборочной компоненты до позиции выгрузки промежуточной сборочной компоненты более сложной структуры, по сравнению с входной промежуточной компонентой, или готового сборочного изделия в целом.

   Авторами в работах [1-3] были сформулированы некоторые предложения, которыми воспользуемся для достижения поставленной цели и, как следствие, для решения поставленных задач. Эти положения, применительно к поставленной цели, будут заключаться в следующем:

   1. Абстрагируясь, представим позиции каждого i-го выходного ротора элементами по отношению к позициям входного ротора.

   2. В каждом i-ом выходном роторе и входном роторе имеется нулевой элемент. Таким элементом является Vi позиция каждого выходного и входного роторов. Заметим, что, переходя от любой img -ой позиции k-го выходного или входного ротора через Vik число позиций, опять возвращаемся к -ой позиции k-го выходного или входного ротора. Это условие может быть записано следующим образом [1].

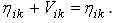
   Это условие объективно отражает процесс рекуррентного перемещения позиций k-го выходного или входного роторов по k-ым замкнутым траекториям этих роторов.

   3.Для любой позиции 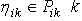k-го выходного ротора существует позиция с номерами такая, что

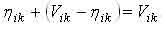
   Здесь позиция выходного k-го ротора является противоположной позиции .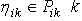

   Предложения 2 и 3 являются необходимыми и достаточными усло-виями того, что каждый выходной ротор, а также и входной, ротор являются циклическими группами. Для достижения поставленной цели необходимо решить задачи, приведенные выше.

   Используя положения алгебры групп, количество различных мар-шрутов промежуточной сборочной компоненты или изделия определится по зависимости

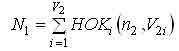
   где n2 - число маршрутов, проходящих через каждый выходной ротор, и определяется по зависимости

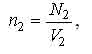
   где V2 - количество выходных роторов;

   N2 - число маршрутов, приходящихся на одну позицию входного ротора без учета количества маршрутов, проходящих по позициям выходных роторов.

   N2 определяется по формуле

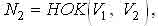
   где V1 - количество позиций входного ротора;

   НОК - наименьшее общее кратное между количеством позиций входного ротора и количеством выходных роторов.

   Совокупность зависимостей (1), (2), (3) дает возможность нахождения общего числа различных маршрутов движения промежуточной сбо-рочной компоненты или изделия.

   Параметры полного кинематического цикла движения промежуточной сборочной компоненты или изделия определяются по следующей зависимости

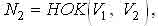
   Здесь НОК(V12,V22,...V2v2)- наименьшее общее кратное и в данном случае определяет количество маршрутов, которое приходится на каждую позицию всех выходных роторов. Остальные значения, входящие в формулу (4), аналогичны по своему содержанию значениям выражения (1).

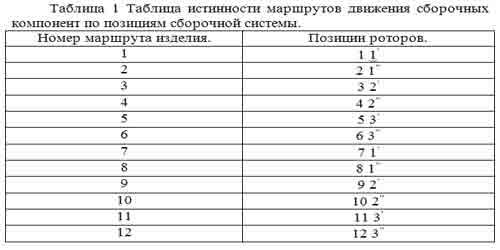
   В качестве примера рассмотрим автоматическую технологическую сборочную систему, состоящую из трех роторов - одного входного и двух выходных. Входной ротор имеет двенадцать позиций, а выходные роторы имеют по три позиции каждый. Количество различных маршрутов определим по формуле (4):

   Найденное количество различных маршрутов соответствует реаль-ному количеству маршрутов, приведенному в таблице 1.

   Определение прохождения промежуточных сборочных компонент по всем позициям входного ротора и выходных роторов проведем в не-сколько этапов. Положение промежуточной сборочной компоненты в зависимости от номера маршрута в входном роторе определяется следующими зависимостями:

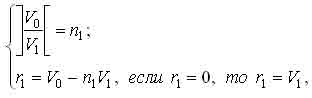
   где V0 - номер маршрута движения промежуточной сборочной компоненты;

   n1- число целых циклов работы входного ротора;

   r1- номер позиции входного ротора.

   Нахождение промежуточной сборочной компоненты в i-ом сборочном технологическом модуле на j-ой сборочной позиции по номеру маршрута движения осуществляется в несколько этапов. На первом этапе необходимо определить положение промежуточной сборочной компоненты относительно выходных роторов, т.е. определить, в каком выходном роторе находится промежуточная сборочная компонента. Определение нахождения промежуточной сборочной компоненты в выходном роторе осуществляется с помощью зависимости:

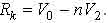
   где Rk - номер выходного ротора;

   n- число целых циклов работы выходного k-го ротора.

   Определение позиции нахождения промежуточной сборочной компоненты или изделия осуществляется на основании следующего выражения

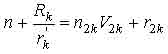
   с необходимыми и достаточными условиями:

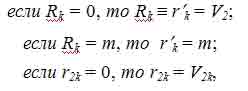
   где n - целое число циклов работы k-го выходного ротора;

    rk - промежуточное значение позиций выходного ротора;

    m -m-ая позиция выходного ротора;

    V2k- общее количество позиций -го выходного ротора;

    r2k - позиция k -го выходного ротора, соответствующая V0 номеру маршрута движения промежуточной сборочной компоненты.

   Зависимости (6), (7) позволяют определить маршруты движения промежуточной сборочной компоненты по всем позициям входного и выходных роторов.

   Разработанные зависимости позволяют определить движение про-межуточной сборочной компоненты в сложных технологических системах по каждой из позиций сборочных модулей, что необходимо для эффективного контроля функционирования этих систем.

Список литературы