The assembly process technology model based on the graph theory and influ-ence of three main flows (energy, information, and material) on the assembly object was proposed. The model allows to minimise the technology assembly process both for each separate flow and all the flows in the whole.
На ранних стадиях разработки технологических процессов сборки в условиях автоматического типа производства появляется задача определения более рационального технологического процесса сборки. Эта задача должна решаться на основании минимального использования трех потоков (материального, энергетического и информационного).
Технологическое преобразование сборочных компонент в изделие достигается целенаправленными совокупными технологическими воздействиями N материального S, энергетического E и информационного I типов [1], которые можно представить следующим образом: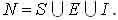

Эти три технологических воздействия осуществляются операторами модели (рис. 1), а именно: надсистемой (исполнителями), автоматической сборочной системой и средой. В связи с этим технологические воздействия можно описать выражениями:

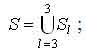
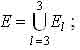
где l - количество операторов модели.
Следует отметить, что входы операторов (исполнители, автоматическая технологическая сборочная система, среда) являются также материального Sv1, Sv2, Sv3 энергетического Ev1, Ev2, Ev3 и информационного Iv1, Iv2, Iv3 типов. При этом названные операторы модели автоматической технологической сборочной системы взаимодействуют между собой и имеют связи материального, энергетического и информационного характеров (ответные и обратные реакции) рис. 1. Заметим, что в модели какой-то тип или группа типов воздействия или связей может отсутствовать, в зависимости от конкретных условий и задач проектирования автоматических технологических сборочных систем. В модели автоматической технологической сборочной системы преобразования над сборочными компонентами выполняются на основе некоторой технологии, представляющей собой упорядоченную совокупность целенаправленных частичных изменений. При этом свойства изделия могут быть получены различными технологиями.
Как известно, технологический процесс автоматической сборки [2] состоит из основных операций, подготовительных (мойка, сушка деталей, контроль, сортировка и комплектация), вспомогательных операций (контроль, поштучное и партионное деление, счет, распределение ...), послесборочных операций (контроль на выходе, заправка смазкой ...).
Основные операции автоматической сборки изделия выполняются на следующих переходах:
1) загрузка сопрягаемых компонент в загрузочные устройства и подача их в предварительно или окончательно ориентированном положении;
2) захват, отсекание и подача в базирующие устройства;
3) ориентация с требуемой точностью;
4) соединение и фиксация с требуемой точностью;
5) контроль выходных параметров;
6) выгрузка и транспортировка собранных изделий.
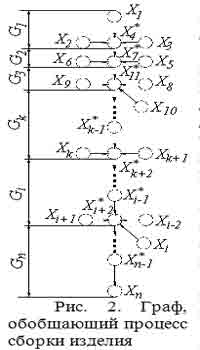
Остановимся на четвертом переходе основной операции автоматической сборки, так как подготовительные, послесборочные операции и другие переходы основной операции не являются доминирующими в технологическом процессе автоматической сборки. Известно [3], что последовательность сборки изделия можно рассмотреть с помощью теории графов.
Рассмотрим абстрактное сборочное изделие, состоящее из n элементов, причем каждый i-ый элемент сборочного изделия представляет собой отдельную сборочную компоненту. Граф такого изделия представлен на рис. 2.
В данном случае каждая сборочная компонента Xj описывается кортежем (e, i, s), состоящим из потоков энергии e, информации i, и материи s.
На первом этапе к элементу x1 присоединяются два элемента x2 и x3 в результате чего получается промежуточная сборочная единица x*4. Если произвести промежуточное деление графа G?n на более мелкие составляющие (подграфы), которые будут заканчиваться промежуточными сборочными единицами x*j, то сборочный процесс получения промежуточного изделия x*j можно представить следующим образом:

На втором этапе к элементу x4* присоединяются элементы x6, x8 и, в ре-зультате получаем промежуточную сборочную единицу x7* (граф G2 (X2, U2)):
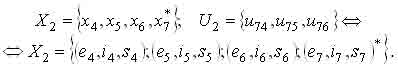
Таким образом поступаем для получения каждой промежуточной единицы x*j, до получения сборочного изделия x*п.
Операция объединения графов будет выглядеть следующим образом:
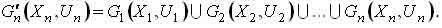

Таким образом формулы (1) и (2), описывающие сборку абстрактного сборочного изделия, отражают обобщенную информационную модель перехода (соединение и фиксация) основной операции технологического процесса автоматической сборки. Формулы (1) и (2), а также сам граф легко позволяют проследить все связи и влияние каждого кортежа на общую характеристику модели, а следовательно, и описываемого моделью исследуемого изделия. При этом большое удобство дает использование матрицы смежности Mс.

Как известно [4], матрица смежности определяет структуру графа. Отметим некоторые свойства матриц смежности [4], используемые при решении практических задач:
1. Нулевые столбцы определяют вершины - истоки, нулевые строки - стоки.
2. Матрица смежности содержит единицы (или другие положительные числа, отличные от нуля) по главной диагонали тогда и только тогда, когда граф имеет петли. Наличие по главной диагонали матрицы только нулей свидетельствует об отсутствии петель.
3. Если отношение числа элементов матрицы, расположенных под главной диагональю (при строго последовательной нумерации вершин), к числу элементов, расположенных над главной диагональю, равно единице, то граф симметричный, если же это условие нарушено, то граф асимметричный.
4. Возведением матрицы в степень можно определить длину всех путей.
Наиболее ценным, в наших условиях, являются второе и четвертое свойства. Наличие петель в структуре графа говорит о том, что промежуточное сборочное изделие, сборочная компонента или сборочное изделие должно получить какое-либо дополнительное воздействие (например: развальцовка самостопорящихся гаек после сборки; кернение резьбовых соединений ...). Определение длин всех путей позволяет определить минимально-необходимое количество «цепочки» технологических воздействий на сборочные компоненты, для получения сборочного изделия. В нашем случае для графа рис. 2 общая матрица смежности представлена выражением (3). Из анализа матрицы смежности следует, что три исходные компоненты x1, x2, x3 формируют промежуточную структурную компоненту x4*; компонента x4* может считаться первичной и является начальной (базовой) для получения промежуточной компоненты x7*; в свою очередь промежуточная компонента x7* может считаться первичной для получения промежуточной компоненты x8* и т.д.
Формирование выводимой структурной компоненты xп* ведется по всем путям последовательно (возможны варианты параллельного, параллельно-последовательного или последовательно-параллельного получения), участвуют все предшествующие ей структурные компоненты модели, общее число которых составляет (p-1), где p - общее количество вершин графа (или сборочных компонент). Приписав единичному элементу матрицы смежности amn, который соответствует связи между компонентами xn и xn, «вес» компоненты xm (дугам unm графа приписываются соответствующие числовые значения), можно получить количественную оценку параметров модели
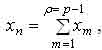
где - p число связей, участвующих в формировании (выводе) компоненты xn.
Аналогично определяется и значение основной компоненты.
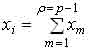
Каждая промежуточная компонента xn (4) модели соответствует завершению определенного этапа формирования изделия при его сборке и определяет порядок модели. Он равен числу дуг графа, соединяющих компоненту xn с наиболее удаленной (по пути) исходной компонентой. Математически порядок xn можно определить через ранг r матрицы смежности Mс. Так как каждая структурная компонента описывается картежом xj = (ej, ij, sj), состоящим из энергетических информационных и материальных потоков, то, вполне допустимо, составить три матрицы смежности. В результате комплексного анализа матриц смежности и каждой в отдельности можно получить полную картину технологического процесса сборки. Для получения полной картины процесса сборки введем кодирование по каждому потоку, определяющее два или более необходимых для качественного процесса сборки уровней.
Для материального потока:
s1 - наличие сборочной компоненты;
s2 - отсутствие сборочной компоненты.
Для энергетического потока:
e1 - отсутствие дополнительных энергетических затрат;
e2 - минимальные дополнительные энергетические затраты;
e3 - средние дополнительные энергетические затраты;
e4 - максимальные энергетические затраты.
Для информационного потока:
i1 - наличие положительной информации о качестве сборки;
i2 - отсутствие или отрицательная информация о качестве сборки.
Приведенные зависимости и использование кодирования позволит на ранних стадиях проектирования технологического процесса сборки и автоматических технологических сборочных систем осуществить минимизацию использования материальных, энергетических и информационных потоков и тем самым выбрать наиболее рациональный вариант технологического процесса сборки.
Список литературы:
1. Хубка В. Теория технических систем. М. Мысль, 1985. – 236 с.
2. Косилов В. В. Технологические основы проектирования автоматического сборочного оборудования. М., «Машиностроение», 1976. - 248 с.
3. Лебедовский М. С., Вейц В. Л., Федотов А. И. Научные основы автоматической сборки. - Л.: Машиностроение, 1985. - 316 с.
4. Берж К. Теория графов и ее приложения. - М.: ИЛ., 1982. - 319 с.