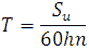 (1)
(1)Источник: Прогрессивные технологии и системы машиностроения:
Сборник научных трудов.
- Донецк, ДонГТУ - 2000. Вып. 10 с. 210-213.
Оценка долговечности зубчатых муфт, применяемых для соединения несоосных валов, представляет интерес при проектировании и эксплуатации их. Срок службы муфты Т в час может быть определен по формуле
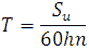 (1)
(1)
где Su – допустимый линейный износ зубьев втулки, мм; n – частота вращения втулки, об/мин; h – линейный износ за один оборот муфты, мм.
Линейный износ h получен решением контактных задач, исследованием кинематики относительного перемещения зубьев и пути трения максимально нагруженных точек зуба втулки [1].
В производственной практике зубчатые муфты выбраковывают, когда износ зубьев достигает (0,1 … 0,15) π m, где m – модуль зацепления. Во многих случаях такой критерий является заниженным. Исследования величин износа муфт, работающих в производственных условиях, показали, что муфты не теряют прочности при износе, достигающем 30…50% толщины зуба. Это объясняется увеличением податливости зубьев при износе и благоприятным распределением нагрузки между зубьями. Допустимый износ зубьев муфты необходимо устанавливать в соответствии с условиями работы муфты и качеством поверхностного слоя зубьев.
Если при изготовлении муфт на зубьях создан качественно отличающийся от основного материала поверхностный слой (закалка ТВЧ, цементирование, азотирование, ППД и т.п.), то допустимая величина износа должна приниматься равной толщине этого слоя. После износа такого слоя в работу вступят слои основного материала, имеющие меньшие прочностные характеристики. При этом вид износа изменится и катастрофически увеличится. Благоприятное распределение нагрузки между зубьями, вызванное увеличением податливости, будет играть второстепенную роль.
При объемной термообработке, когда качество материала зубьев имеет одинаковые характеристики во всех сечениях, вид и темп износа сохраняется постоянным и на допустимую величину износа оказывает существенное влияние распределение нагрузки между изношенными зубьями.
При определении допустимой величины износа Su принято следующее положение. Вследствие износа зубьев увеличивается их податливость, что приводит к уменьшению нагрузки на зубья. Напряжения в корне зуба уменьшаются. Такое положение сохраняется до определенной критической толщины зубьев, при которой происходит увеличение напряжения в корне зуба и его поломка. Следовательно, износ зубьев допустим до момента, когда изгибные напряжения не превышают расчетных, то есть при условии
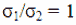 (2)
(2)
где σ1 и σ2 соответственно изгибные напряжения в новой и изношенной муфте.
На основании гипотезы А. В. Верховского о неискривляемости при изгибе ломаных сечений, нормальных переходной кривой у основания зуба, изгибные напряжения определяются по зависимости
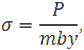 (3)
(3)
где P – нагрузка на зуб, b – ширина зуба, y – коэффициент формы зуба при расчете на излом по местным напряжениям зубьев из анизотропного материала.
Сформулируем условие совместности перемещений. Перемещение точки контакта δi+1 1-ой пары зубьев в направлении нормали должно отличаться от перемещения δi точки контакта і –ой пары зубьев на величину разности зазоров ji+1 и ji между этими парами зубьев
Коэффициент y является геометрической характеристикой зубьев и уменьшается при износе зубьев. Так как m и b являются постоянными величинами, то изгибные напряжения в корне зуба определяются отношением нагрузки и размерами зуба. С учетом (2) и (3) получим
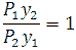 (4)
(4)
Нагрузка Р1 на зуб на оси наибольших перекосов без учета погрешностей изготовления для новой муфты равна [2]
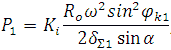 (5)
(5)
где Ki = Ci/Co – коэффициент, учитывающий изменение жесткости при изменении угла положения зуба; Ci – жесткость і-го зуба; Co – жесткость зуба на оси наибольших перекосов; δΣ 1 – полное перемещение обыкновенной точки поверхности зуба от единичной нагрузки; Ro – радиус бочкообразности зубьев; ω – угол перекоса сопрягаемых валов; φk – угол зоны контакта зубьев; α – угол зацепления.
Для изношенной муфты Р2 равно
 (6)
(6)
С учетом (4), (5) и (6) получим
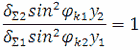 (7)
(7)
Так как коэффициент формы зуба y представляет собой геометрическую характеристику зуба, то можно принять, что
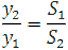 (8)
(8)
где S1 и S2 – соответственно толщина зуба новой и изношенной муфты.
Тогда
 (9)
(9)
Существует определенная закономерность, связывающая отношения δΣ 2/ δΣ 1 и S1/S2.
Для выявления указанных закономерностей проведен эксперимент, в котором фиксировались изменения податливости зубьев и изгибных напряжений при изменении толщины зубьев.
Экспериментальная зубчатая муфта имела втулку с двумя диаметрально противоположными зубьями m = 3 (рис. 1). Обойма и втулка выполнялись из оргстекла. Один зуб имел на торце прослойку из оптически активного материала толщиной 1 мм, позволяющую определять изгибные напряжения методом фото-упругости в условиях деления компенсатора. Деформация зубьев δΣ измерялась индикатором часового типа с ценой деления 0,005 мм.

Рис. 1. Схема эксперимента.
Анализ геометрии изношенных зубьев муфты показал, что в процессе износа они приобретают в поперечном сечении треугольный профиль.
Такая геометрия экспериментальных зубьев обеспечивалась шлифованием их на заточном станке 3А64. В таблице 1 приведены значения толщины зубьев и соответствующие им деформации и изгибные напряжения.
Таблица 1 – Деформация зубьев и изгибные напряжения от толщины зубьев
| № эксперимента | Толщина зуба, S мм | Деформация зуба, δΣ мм |
Изгибные напряжения σ в условных делениях компенсатора |
| 1 | 8,80 | 0,096 | 69,4 |
| 2 | 7,80 | 0,115 | 73,2 |
| 3 | 6,70 | 0,125 | 92,9 |
| 4 | 6,00 | 0,135 | 100,0 |
| 5 | 5,25 | 0,153 | 118,4 |
| 6 | 4,40 | 0,140 | 150,0 |
| 7 | 3,5 | 0,185 | 164,3 |
В таблице 2 приведены относительные значения толщины зубьев, деформаций и изгибных напряжений к полной толщине зуба.
Таблица 2 - Относительные значения толщины зубьев, деформаций и изгибных напряжений
| № эксперимента | SΔ = S1/S2 | Kа = δΣ 2/ δΣ 1 | δ 1/ δ 2 |
| 1 | 1,00 | 1,00 | 1,00 |
| 2 | 1,13 | 1,18 | 1,05 |
| 3 | 1,31 | 1,29 | 1,34 |
| 4 | 1,46 | 1,39 | 1,50 |
| 5 | 1,67 | 1,58 | 1,71 |
| 6 | 2,00 | 1,44 | 2,16 |
| 7 | 2,51 | 1,91 | 2,50 |
Графические зависимости, построенные по результатам таблиц 1 и 2 позволяют предполагать между δΣ 2/ δⓗ 1 и S1/S2 линейную зависимость. Обработка экспериментальных данных позволила получить экспериментальную зависимость
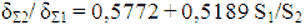 (10)
(10)
Полученное выражение (10) совместно с (9) дают возможность получить формулу для определения допустимой толщины зуба зубчатой муфты, обеспечивающей необходимую прочность зуба на излом:
 (11)
(11)
Этот критерий объективно отражает условия работы муфты по сравнению с допустимой величиной износа определяемой зависимостью (0,1 … 0,15) π m, т.к. он учитывает уровень нагрузки на зубья муфты при передаче крутящего момента.
Польченко В.В., Михайлов А.Н. Износ в зубчатых муфтах. Прогрессивные технологии и системы машиностроения: Сб. научных трудов. – Донецк: ДонГТУ, 1997. Выпуск 4. – С. 131-135.
Польченко В.В. К расчету зубчатых муфт на долговечность // Теория и практика расчетов деталей машин на износ. - М.: Наука, 1983.