Дисперсионный анализ исследования сопряжения вала с корпусом

Теряев Е.А., Коваленко В.И.
Донецкий национальный технический университет

Источник: Известия ТРТУ-ДонНТУ. Материалы Одиннадцатого Международного научно-практического семинара "Практика и перспективы развития партнерства в сфере высшей школы", г. Таганрог. Издательство ТРТУ, 2010

В заводских условиях произведено экспериментальное исследование сопряжения вала с корпусом. На рис. 1 представлена схема кривошипно-шатунного механизма. Исходным для данного механизма является вращательное движение вала 1, на конце которого расположен кривошип 2, эксцентриситет которого равен e. Вращательное движение кривошипа преобразуется в возвратно-поступательное движение шатуна 3 и поршня 4. Для исследования принято сопряжение двух поверхностей вала 1 (диаметры которых d_в1 и d_в2) с отверстием корпуса 5 (средний диаметр отверстия обозначен D_ср)

В условиях крупносерийного производства производится финишная обработка отверстия на хонинговальном станке модели ВСМ30Н417 хонинговальной головкой с алмазными брусками АСМ 14/10 100 М1 ГОСТ 25594-83, а также обработка поверхностей коленчатого вала (сопрягаемых с корпусом) на специальном бесцентровом модуле модели ВШ-727 РМН 153. Материал заготовки вала – высокопрочный чугун ВЧ400-15 ДСТУ 3925-99, корпуса – серый чугун СЧ25 ГОСТ 1412-85.

В цехе селективной сборки обрабатываемые детали измеряются и сортируются на 3 селективных группы; затем детали поступают в сборочный цех. Численные значения селективных групп приведены в табл. 1.

Таблица 1. Селективные группы сопрягаемых деталей

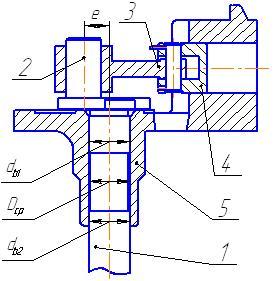
Оценка результатов измерений производилась с использованием выборок. Было проанализировано 3 выборки, в каждой из которых фиксировались значения d_в1, d_в2, D_ср. Выборки выбирались с периодичностью одна неделя.

Диаграммы распределения размеров по первой выборке для параметров d_в1, d_в2 представлены на рис. 2, а для среднего диаметра D_ср - на рис. 3.

Для каждой выборки определялись зазоры J₁ и J₂ как разность размеров среднего диаметра отверстия и диаметров соответствующих поверхностей вала. Диаграмма распределения зазоров J₁ и J₂ по первой выборке представлена на рис. 4.

Для проверки однородности двух дисперсий на практике чаще всего используют критерий Фишера (F-критерий), который заключается в том, что берется отношение большей дисперсии (S₁²) к меньшей (S₂²) [1]:

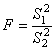(1)

Расчётное значение критерия сравнивается с критическим табличным, определяемым для принятого уровня значимости и соответствующих S₁² и S₂² степеней свободы f₁ и f₂. Если расчётное значение F меньше табличного F_α, то дисперсии однородны; в этом случае необходимо пользоваться средневзвешенным значением дисперсии:

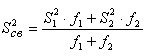(2)

Характеристики выборок (объём выборки n, число степеней свободы f, среднее арифметическое X и оценка дисперсии S_x²) представлены в табл. 2.

Таблица 2. Статистические характеристики выборок

В качестве примера определим однородность выборок по параметру d_в1.

Расчётное значение критерия Фишера для выборок №№ 1 и 2, определенное по формуле (1) составило Fрас_1-2=2,489 ⁄ 1,494=1,666.

Табличное значение критерия Фишера [2] для степеней свободы f₁=49 и f₂=49 Fтабл=1,607.

Так как расчетное значение критерия больше табличного, значит, выборки №№ 1 и 2 неоднородны, и необходимо сравнивать выборки №№ 1 и 3. Аналогично предыдущему расчету определяем: Fрас_1-3=2,5 ⁄ 1,494=1,673 и при f₁=49 и f₃=49 Fтабл=1,607. Расчетное значение критерия больше табличного и, следовательно, выборки №№ 1 и 3 также неоднородны.

Сравниваем выборки №№ 2 и 3: Fрас_2-3=2,5 ⁄ 2,489=1,004 и при f₂=49 и f₃=49 Fтабл=1,607.

Итак, расчётное значение критерия меньше табличного. Значит, дисперсии однородны и необходимо дисперсии соответствующих выборок заменить на средневзвешенную дисперсию. Согласно формуле (2):

Далее сравниваем средневзвешенную дисперсию с дисперсией выборки №1: Fрас_св-1=2,494 ⁄ 1,666=1,496 и при f_св=99 и f₁=49 Fтабл=1,53, расчётное значение критерия меньше табличного, значит дисперсии однородны.

Итак, все 3 выборки относятся к одной генеральной совокупности. Аналогичным образом проводились дисперсионные анализы выборок по параметрам: d_в2, D_ср, J₁, J₂.

Библиографический список

1. Справочник по теории вероятностей и математической статистике / Королюк В.С., Портенко Н.И., Скороход А.В., Турбин А.Ф. – М.: Наука. Главная редакция физико-математической литературы, 1985.

2. Теория инженерного эксперимента: Учеб. пособие / Тимошенко Г.М., Зима П.Ф. – К.: УМК ВО, 1991.

3. Микулик Н.А., Рейзина Г.Н. Решение технических задач по теории вероятностей и математической статистике: Справ. Пособие. – Мн.: Выш. шк., 1991.