Теория планирования многофакторных экспериментов - резерв повышения эффективности технологических процессов

Нечаев К.Н.
Санкт-Петербургский институт машиностроения (ЛМЗ-ВТУЗ)

Источник: Российский научно-технический журнал "Инструмент и технологии" - Санкт-Петербург, 2008. №25 вып.1, стр. 140-145

The basic ideas are resulted and advantages of methods of the theory of planning of multifactorial experiments are shown at researches of technological processes. Examples of application of these methods for the analysis and show optimization of various processes of processing of metals, that these methods are an essential reserve of increase of efficiency of technological processes.

Высокая производительность и качество механической обработки деталей при минимальной себестоимости могут быть достигнуты при условии, что технологический процесс (ТП), инструмент и режимы резания являются оптимальными для данных условий обработки.

Это положение особенно актуально при выполнении наиболее ответственных финишных операций (тонкое точение, шлифование, хонингование и др.), при разработке новых ТП и обработке новых, в частности труднообрабатываемых материалов (нержавеющие и жаропрочные стали, сплавы титана и т.д.).

Под оптимальными режимами понимают такое сочетание значений факторов ТП, при которых ожидается наилучшее значение параметра оптимизации.

В качестве параметров оптимизации ТП могут быть приняты:

а) показатели качества обработки(точность, шероховатость, и т.д.);

б) показатели производительности и себестоимости обработки;

в) показатели стойкости режущего инструмента, усилия, температура резания и другие.

В качестве факторов ТП могут рассматриваться физические и механические характеристики материалов обрабатываемой заготовки и инструмента, элементы режимов резания, геометрии режущего инструмента, применяемые СОТС и т.д.

Решение задачи оптимизации ТП на практике затруднено недостаточной информацией об исследуемом процессе и наличием большого числа факторов х_i, влияющих на параметры оптимизации y_j.

Эти обстоятельства практически исключают теоретический путь решения задачи оптимизации конкретных ТП. Экспериментальный путь решения этой задачи становится наиболее реальным с использованием прогрессивных методов теории планирования многофакторных экспериментов (МФЭ) [1],[5],[11],[12].

Использование этих методов позволяет не только построить математические модели используемых ТП в виде уравнений:

но и выполнить оптимизацию параметров y_j при проведении экспериментов.

МФЭ в отличие от классического (1-факторного) метода позволяет одновременно учитывать всё множество действующих факторов, при этом в каждом опыте варьируют одновременно все факторы на разных уровнях в соответствии с принятым планом. При этом большинство разработанных планов МФЭ являются оптимальными как по числу опытов, так и по точности эксперимента.

Основные идеи теории планирования МФЭ состоят в следующем.

Исследуемый ТП представляется в виде «чёрного» ящика – рис.1 , на входе которого имеется множество факторов Х₁,Х₂, … Х_n , а выход характеризуется параметрами y₁,y₂, … y_k.

Рис. 1. Схема «чёрного» ящика

Искомые параметры в области факторного пространства представляют в виде разложения в ряд Тейлора по степеням факторов, при этом оценки коэффициентов ряда находят в результате статистической обработки заранее спланированного и проведённого МФЭ. В итоге получают уравнение регрессии (функцию отклика):

которое и является математической моделью исследуемого ТП.

Теоретической основой для нахождения коэффициентов b₀,b_i, b_ij, b_ii служит метод наименьших квадратов, для корректного применения которого необходимо соблюдать ряд предпосылок [1]. Наш анализ показал, что для большинства ТП преимуществами МФЭ являются:

а) чёткий план проведения эксперимента;

б) обработка результатов МФЭ формализована, в связи с чем её возможно проводить на ЭВМ;

в) с увеличением числа факторов точность эксперимента повышается;

г) число необходимых опытов снижается в 3…10 раз по сравнению с классическим методом (при одинаковой точности обоих методов);

д) по аналитической зависимости (2), полученной при обработке результатов МФЭ, можно оценить влияние каждого из факторов х_i на исследуемый параметр y_j, что создаёт предпосылки для управления и оптимизации исследуемого ТП.

Отмеченные преимущества МФЭ определяют высокую эффективность их применения в практике технологии машиностроении и других отраслях производства.

Наши исследования [3],[4] показали широкий спектр возможных областей применения МФЭ в технологии машиностроения, в частности МФЭ используют для решения следующих практических задач:

а) технологии металлов и композиционных материалов (литьё, обработка давлением, порошковая металлургия, производство биметаллов и т.д.);

б) сварки (практически все виды), склеивания, термообработки, нанесения покрытий, и т.д.;

в) обработки резанием (практически все её виды);

г) разработки и внедрения нетрадиционных ТП (пластическое деформирование, ротационная вытяжка, вибрационная обработка, термофрикционная обработка, электрофизические методы обработки и т.д.)

В настоящее время автор располагает банком данных, содержащим более 300 примеров применения МФЭ в технологии машиностроения и других отраслях промышленности.

Наш анализ показал, что наиболее широко при этом применяют следующие планы и методы теории планирования МФЭ:

1) планы первого порядка: ПФЭ (полного факторного эксперимента) и ДФЭ (дробного факторного эксперимента);

2) планы второго порядка: ОЦКП (ортогонального центрального композиционного плана) и РЦКП (рототабельного центрального композиционного плана);

3) оптимизация методом крутого восхождения(КВ) или симплексного планирования(СП).

Если ожидаемая математическая модель имеет вид:

то рекомендуется план ПФЭ типа 2^k, где 2 – число уровней варьирования каждого из факторов, k – число факторов.

Если математическая модель ожидается в виде:

то допустимо ограничиться планом ДФЭ типа 2^k-p ,где p – число факторов, приравненных к взаимодействию (априорно незначимому) других факторов.

Если математическая модель ожидается в виде:

то применяют планы ОЦКП или РЦКП. Эти планы строят на основе ПФЭ с добавлением опытов в центре плана и в «звёздных» точках (их координаты находят по соответствующим формулам).

Оптимизация методом КВ производится на основе математической модели вида (3) или (4) с последующим движением в направлении градиента исследуемого параметра. Метод СП не требует предварительного получения модели процесса и предполагает последовательное движение в направлении, противоположном наихудшему значению параметра, полученному в предыдущей серии опытов.

Построение планов I и II порядка, а также алгоритмы КВ и СП формализованы. Однако при планировании и проведении МФЭ необходимо учитывать и ряд неформализованных этапов [1], [8].

Рассмотренные планы и методы МФЭ позволяют решать следующие практические задачи:

а) анализ ТП обработки (по уравнению регрессии);

б) установление контролируемых параметров ТП;

в) оптимизация ТП.

Различные примеры и рекомендации по применению методов теории планирования МФЭ в технологии машиностроения приведены в [3], [4], [8],[12].

Так, в [12] решали задачу оптимизации ТП токарной обработки. В качестве параметра оптимизации y принята стойкость Т (в минутах) резца при обработке стали в заданном режиме. Исследовали влияние пяти факторов геометрии резца (углы γ, α, φ₁, φ и радиус при вершине r).

Для решения этой задачи использовали план ДФЭ типа 2^5-2 и метод КВ. В итоге было достигнуто повышение стойкости резца на ≈60% и определены оптимальные значения факторов, соответствующие максимальной стойкости.

Для достижения этого результата потребовалось всего 15 реальных опытов, т.е. условно на каждый из факторов пришлось по три опыта.

В другом примере [8] выполняли оптимизацию центровочных свёрл диаметром 4мм из стали Р6М5. Для трёх факторов геометрии сверла был реализован план ПФЭ типа 2³ с последующим КВ. В итоге было достигнуто повышение стойкости свёрл в 6,5 раз, для чего потребовалось 11 опытов.

Задача исследования процесса торцевого сверхскоростного фрезерования бронзы Бр АЖ9-4 решалась в [7]. Исследовали влияние трёх факторов (V – скорости резания в диапазоне от 52,5 до 77,5 м/с, S – подачи на зуб в диапазоне от 0,025 до 0,05мм и t – глубины резания в пределах от 0,3 до 0,7мм ) на параметр y = R_a – среднее арифметическое отклонение профиля шероховатости.

Эксперимент был поставлен по плану РЦКП. Полученная математическая модель имеет вид:

Этот эксперимент позволяет по уравнению (6) выявить влияние каждого из факторов на параметр R_a, и затем перейти к оптимизации.

Эффективной представляется оптимизация методом СП. Симплекс – это геометрическая фигура, имеющая в к-мерном пространстве к+1 вершину.

План МФЭ при СП – это совокупность к+1 опытов, условия проведения которых задают координатами вершин симплекса. Перемещение симплекса в факторном пространстве ведут путём зеркального отображения вершин, имеющих наихудшее значение параметра у. Координаты новой точки, в которой ставится следующий опыт, находят по соответсвующим формулам[8].

Достигнув области оптимума, симплекс начинает вращение вокруг вершины с наилучшим значением параметра у, что является признаком завершения процесса оптимизации.

В [8] методом СП решали задачу оптимизации режимов резания при сверлении отверстий. Варьировали n – число оборотов шпинделя и подачу s.

Схема движения симплекса приведена на рис. 2. В данном случае наибольшая стойкость сверла достигнута в точке В^** (опыт №7) и составляет 24,8 мин., т.е. по сравнению с исходной стойкость возросла в 2,7 раза. Оптимальный режим резания составляет S=0,005 мм/об и n=6060 об/мин.

Приведённые примеры свидетельствуют о высокой эффективности применения научно обоснованных методов планирования МФЭ для исследования и оптимизации различных ТП механической обработки.

Однако эти методы ещё недостаточно используются при решении конкретных задач производства. Одной из причин такого положения является небольшое число специалистов, владеющих этими методами, а также недостаточный уровень подготовки инженерных кадров в этой области.

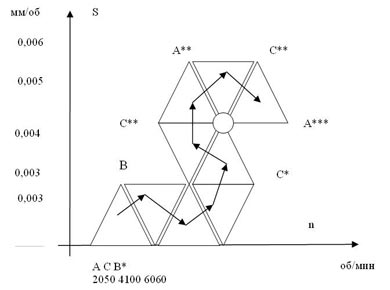
Рис. 2. Схема движения симплекса

Кафедра «Технологии машиностроения» Санкт-Петербургского института машиностроения оказывает консультации и сотрудничает с предприятиями в решении конкретных задач производства с применением методов планирования МФЭ.

Кафедра использовала эти методы при исследовании процессов резания и шлифования [6]. Данные работы выполняются с 1998 г. в кафедральной отраслевой научно-технической лаборатории «Высокоскоростной лезвийной и абразивной обработки».

В настоящее время автор использует МФЭ при исследованиях перспективных методов термофрикционной обработки [9], [10]. В [2] МФЭ применили для исследования процесса термофрикционного формообразования отверстий.