Библиотека

ИССЛЕДОВАНИЕ НЕЛИНЕЙНОЙ ДИНАМИЧЕСКОЙ СИСТЕМЫ АСИМПТОТИЧЕСКИМ МЕТОДОМ А.Н. КРЫЛОВА

Чернышев Е.А., Волосенко К. Донецкий национальный технический университет, г. Донецк, Украина

Рассматривается нелинейная консервативная автономная система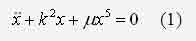

с малым параметром при начальных условиях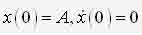

вырождающаяся при м=0 в линейный осциллятор с периодическим порождающим решением периода 2П/к .

В разложении по степеням параметра м , следуя методу А.Н. Крылова [1, 2], функции и квадрата искомой частоты будем искать решение с точностью до второго приближения (включительно):

где коэффициенты h выбираются из условия периодичности функций ф(t) .

Подставив (2) в (1) и приравняв коэффициенты при одинаковых степенях м , получим рекуррентные линейные дифференциальные уравнения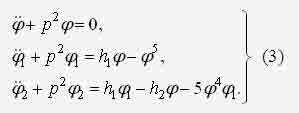

Начальные условия уравнения (1) будут выполнены, если функции ф1,ф2,ф3 будут удовлетворять начальным условиям

Из первого уравнения (3) находим

Подставим это решение во второе уравнение (3), с учетом того, что

и получим.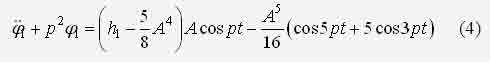

Чтобы исключить вековой член, полагаем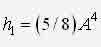

после чего решение уравнения (4) будет иметь вид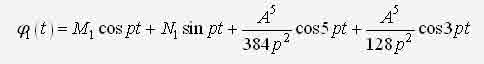

При нулевых начальных условиях

следовательно,

где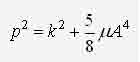

Чтобы получить второе приближение, подставляем найденные ф,ф1 в третье уравнение (3). Воспользуемся тем, что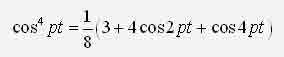

и после некоторых элементарных преобразований получим

Чтобы исключить вековой член, полагаем

откуда

Из уравнения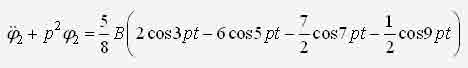

находим, что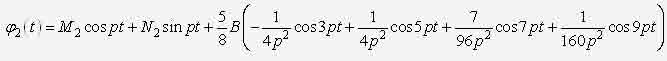

При нулевых начальных условиях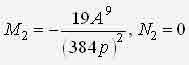

Таким образом,

и во втором приближении решение имеет вид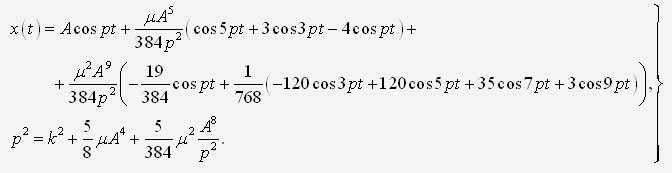

Для нахождения квадрата собственной частоты нужно решить второе уравнение, квадратное относительно р2 . Решив его, получим, что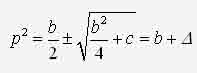

где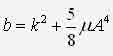

т.е. квадрат собственной частоты в первом приближении;

обусловливающая поправку второго приближения.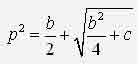

Оценим точность асимптотического решения путем сравнения вычис-ленного периода с найденным численным методом (до пятого десятичного знака). Использовался метод Рунге-Кутты четвертого порядка с шагом интегрирования .

Пусть в уравнении (1) к=1,м=0.1,А=1. Очевидно, что период порождающей системы Т0=2П=6.28319. В первом приближении Т1=6.0955 , во втором приближении Т2=6.0523 . Результат численного решения Т'=6.09672 . Первое приближение имеет относительную погрешность с численным решением 0,019%, второе приближение – 0,024%.

Таким образом, при анализе рассмотренной системы следует ограничиваться первым приближением, получить которое довольно просто. Дальнейшее асимптотическое разложение оказывается излишним и приводит к уменьшению точности.

Список литературы:

1. Бабаков И.М. Теория колебаний / И.М. Бабаков. – М.: Наука, 1968. – 559 с.

2. Андронов А.А. Теория колебаний / А.А. Андронов, А.А. Витт, С.Э. Хайкин. – М.: Наука, 1981. – 568 с.