Включенный подход для разработки SDH петлевых сетей восстановления

Mario Pickavet, Piet Demeester

Автор перевода: Аршинова О.А.

Источник английской версии статьи: http://upload.com.ua/get/901729651/

Краткое изложение

Петлевые сети восстановления, основанные на SONET (Синхронная Оптическая Сеть, стандартная оптическая технология передачи, широко применяемая и используемая в Северной Америке) или SDH (Синхронная Цифровая Иерархия, Европейский стандарт, в настоящий момент принятый главными Европейскими операторами телекоммуникаций), - это экономично привлекательное решение в областях, где высокий спрос и высокая связность внедряется (Wu, 1995). В этих сетях, способность конфигурации систем повторного цифрового соединения (DCS) позволяет перенаправить запрос, которому было отказано сетью. Степень совместного использования пропускной способности в сетях, основанных на этой архитектуре, очень высока.

Эта статья представляет эвристический алгоритм для решения наиболее оптимального проекта петлевого типа SDH связи восстановления сети, т.е. определение топологии сети и назначение вместимости, чтобы перенаправить запрос в нормальных ситуациях и позволить полную связь восстановления в случае отказов связи. Алгоритм основан на технике резкого подъема вверх, новом подходе, который формирует компромисс между последовательным и интегрированным оборудованием. Различные блоки построения алгоритма интенсивно проверены и сравнены с другими результатами, упомянутыми в литературе. Сравнение похожих результатов для данной проблемы проекта с другим оборудованием решения указывает, что включенный метод резкого подъема вверх - это совершенно многообещающий подход, способный объединить точность интегрированных подходов со скоростью вычисления последовательных подходов.

Ключевые Слова: возможность проект, генетический алгоритм, восстановление связи, топология проекта, включенная техника резкого подъема вверх.

1. Введение

Проблема, изучаемая в этой статье, - это проект SDH петлевых сетей восстановления. Данная статья является набором расположений узлов и запросом от узла к узлу VC-4 (1 VC-4 соответствует битовой частоте - 155 Mbit/s). Спрашивается, определение между какими узлами сети должна устанавливаться (проект топологии) связь, как послать запрос (проект послания) и какая вместимость должна быть предназначена для каждого сеанса связи (емкостный проект). Установленная вместимость должна быть достаточной, чтобы нести запрос, не только, когда все компоненты сети функционируют должным образом, но и в случае единого отказа связи. Механизм, используемый для перенаправления запроса, в связи с отказом связи, - это восстановление связи: эффективные соединения достигаются между конечными точками отказа (разрыва) связи.

Установка связи с определенной вместимостью VC-4 между двумя узлами охватывает установку кабеля между теми узлами и достаточным числом оптоволоконных систем. Оптоволоконная система состоит из системы линий и в конечном счете регенераторов на определенном расстоянии вдоль кабеля, чтобы обновить потерянный и искаженный сигнал. Соответственно, три компонента стоимости учитывалось (включая стоимость оборудования и стоимость установки): кабельная стоимость, стоимость системы линии и стоимость регенератора. Кабельная стоимость грубо пропорциональна к расстоянию между узлами. Относительно стоимости систем линии и регенераторов, мы считали системы волокна STM-1 (155 Mbit/s), STM-4 (622 Mbit/s) и STM-16 (2.5 Gbit/s). Экономия в масштабе играет роль в выделении систем линии. Например, STM-4 предлагает вместимость, которая четырежды выше, чем STM-1 и по крайней мере в 2 раза дешевле по стоимости (подобное взаимоотношение поддерживаются между STM-16 и STM-4). В результате, когда поток VC-4, предложенный к сети, относительно высок, можно ожидать доминирующего использования систем линии STM-16, STM-4 и STM-1, они могут быть установлены, когда STM-16 будет строго недогружен. Стоимость регенераторов зависит от типа используемого волокна, но и показывает пошаговою зависимость от длины кабеля.

Чтобы измерить производительность потенциального метода решения для комплексной проблемы проекта сети, описанной выше, отдельные аспекты должны быть приняты во внимание. Самый важный элемент это, конечно, качество найденных решений (т.е., низкая стоимость). Однако, также другие особенности, связанные с доступными ресурсами вычисления, как например время вычисления и требования памяти, оказываются обязательными, чтобы проводить правильное сравнение между различными алгоритмами. Несмотря на природу процесса проекта сети off-line, скорость вычисления важна, потому что это ограничивает размер проблемных случаев, которые могут решаться в пределах "разумного времени". Также требования памяти алгоритма могут сформулировать ограничение на размер проблем, которые могут решаться на практике. В зависимости от специфического алгоритма и доступных ресурсов, или время вычисления или использование памяти может быть самым ограничивающим фактором.

Целый ряд проблем связанных с проектом сети раскрыт в литературе. С одной стороны, запасная емкостной проблемы назначения в петлевых сетях восстаовления затронута многими авторами, смотри например Grover, Bilodeau, и Venables (1991), Herzberg (1993), Herzberg, Bye, и Utano (1995), и Poppe и Demeester (1998). Начиная от данной топологии сети и данного отказа связи, эта статья описывает алгоритмы, чтобы локализовать пропускную способность к различным типам отказа и восстановительным механизмам. С другой стороны, наша проблема также связана с проектом выживающих сетей, изучаемых например в Minoux (1981), Gavish и других (1989), и Stoer и Dahl (1994). Эта статья предполагает, что нет взаимосвязи между посланием запроса в область отказа и послании запроса в случае отказа. Формулировки, которые изучались, навязанные осуществлением мульти-потока в каждой области (без отказов и с отказами)сети, которые действительны согласно с предположением, что там, нет ограничения на пути сети и может переконфигурироваться после того, как отказ произошел. Это стратегия перенаправления контрастирует с ситуацией возобновления связи, где ясная взаимосвязь прослеживается между посланием отказа и посланием в каждую область отказа: трафик, который не затронут (связь) отказом, не может быть перенаправлен и задействованный трафик может только перенаправляться между конечными точками связи и оборванной линией.

Эта статья представляет новый алгоритм, который объединяет проект топологии и емкостное назначение в случае строгого взаимоотношения между посланием в сеть отказа и в сетях отказа, основанных на парадигме восстановления связи. В Poppe и Demeester (1997) подобная проблема описана и представлена основанным алгоритмом Целочисленного Линейного Программирования. В дальнейшем, мы сравним результаты двух подходов при любой возможности.

Статья структурирована как указано ниже. Два главных блока построения алгоритма - это тип Генетического Алгоритма, который разрешает более абстрактную, делаемую способным к выживанию, проблему проекта сети и алгоритм, чтобы локализовать дополнительную вместимость, описанную в Секциях 2 и 3, соответственно. Полный алгоритм (Секция 4) основан на Включенной стратегии резкого подъема вверх, технике, которая формирует компромисс между последовательным подходом и интегрированным подходом. В Секции 5 некоторые цифровые примеры описаны и внимание обращается на относительную важность различных фаз алгоритма. Главные блоки построения алгоритма проверены в Секции 6 и главных предположениях на которых Включенный алгоритм основан на подсвечивании. Качество полного решения сравнено с результатами другого оборудования. Секция 7 включает статью.

2. Абстрактный Самовосстанавливаемый Проект Сети (ACSND)

Один из модулей, используемых в полном алгоритме (описанном в Секции 4), - алгоритм решения более абстрактной проблемы проекта сети ACSND. Оригинальная проблема, заявленная в Секции 1, есть таким образом, слегка адаптированная, чтобы развивать скорость алгоритма.

Во-первых, используется модель стоимости линеаризации. Это руководство к представлению стоимости сети как суммы затрат связи, которые являются функциями длины биллинирования и вместимостью связи.

Во-вторых, используется более абстрактная стратегия послания, которая только косвенно объединяет дополнительную вместимость, которая нужна для возобновления связи. Вместимость связи высчитывается повторно масштабирующей матрицей (например, умножение всех спросов от узла к узлу равно коэффициенту 1.2) спроса и деление трафика вдоль самого короткого пути. Философия после этой bi-посылающей стратегии такая, что в случае единого отказа связи как минимум n/2 частицы не будет эффективна, в то время как оставшаяся частица 1 - n/2 может (частично или полностью) восстанавливаться, используя некоторую запасную вместимость, доступную в сети, если n > 1.

Эти предположения приводят нас к простой оптимальной емкостной процедуре назначения для исправленной топологии: использование минимального алгоритма (Ahuja, 1993) стоимости потока каждый d запроса послано через сеть с затратами на связь с2 + c3*l(e) (единственные компоненты стоимости, которые зависят от емкостного назначения и на движении трафика) и d/2 вместимости связи (чтобы гарантировать bi-направление самым коротким способом). Это позволяет быстро оценить полный c(N) стоимости сети для определенной топологии, таким образом, что мы можем сосредоточиться на выборе хорошей топологии.

Чтобы разрешить проблему ACSND, Генетический Алгоритм, увеличенный с некоторыми определенными шаблонами оптимизации, используется. Мы обращаемся к Pickavet и другие. (1997) для детального описания алгоритма. Главные блоки строительства алгоритма ACSND показаны на рисунке.

Генетический Алгоритм (Голландия, 1975) - это общая техника оптимизации, которая имитирует генетическую эволюцию видов. Главная разница с другим А. I. Подходами, касательно Симулирующего Обжигания примера или Tabu Поиск, есть то, что Генетический Алгоритм имеет дело с 'population' решениями (решение называется 'chromosome') скорее, чем с единым решением. В случае проблемы ACSND, хромосома - это фактически топология сети. Задача - создать топологию с минимальным полным c(N) (и с как минимум – связность = 2) стоимости сети.

Топология сети в начальном виде создается с помощью случайного выбора некоторых связей. Некоторые хромосомы прибавляют к этому виду с помощью применения некоторых действий кросскоммутации и изменения операций. Операция crossover соединяет две существующие хромосомы, чтобы создать новую (и многообещающе лучшую) одну, тогда как действие мутации (изменения) создает новую хромосому с помощью изменения существования одной. Вне этого расширенного вида, состоящего из так называемых родителей, детей и мутантов, новый вид выбирается согласно принципа – выживает сильнейший: хромосомы (т.е., топология с как минимум связность = 2 и низкий c(N) стоимостью сети) высокого качества имеют высшую вероятность избрания для следующей генерации. Эта последовательность действий crossover, действия мутации и выделения нового поколения повторяется, пока никакие лучшие решения не найдены в течение целого ряда генераций. Вне всех генераций, лучшее решение сохранено как заключительное решение проблемы ACSND.

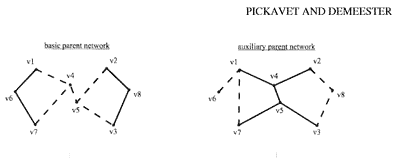
Важно узнать построение блоков (Голландия, 1975) решения высокого качества, для того, чтобы определить действие crossover, которое объединяет хорошие особенности родителей, и исключает плохие особенности. Мы окончательно выбрали сорт cut-and-paste на топологии сети: мы заменяем плохую части одной топологии соответственной частью другой топологии. Это иллюстрировано на проблеме примера 8-узла в рисунке 2. Слабость основной сети родителя является единая связь между v4 узлами и v5 ведущей к низкой надежности: если связь разрывается, сеть будет поделена на две несоединенные части. С помощью замены части сети вокруг той слабой (все связи, которые свойственны v4 узлу и/или v5, брошенные линии в основной сети родителя) соответственной частью другой сети (все связи, которые свойственны v4 узлу и/или V5, полные линии во вспомогательной сети родителя), мы создаем сеть ребенка, которая многообещающе более надежна, чем оба родителя. Чтобы решить какой сrossovers будет принимать участие в популяции, мы сначала проверяем какие хромосомы родителя дополнительные, т.е., плохие части двух топологий должны частично не использоваться. От этих пар кандидата дополнительных родителей, исправленное число пар случайно выбрано, для каждой пары основная сеть родителя случайно назначена и одна хромосома ребенка создана за пару.

При определении подходящего действия мутации, важно, ввести некоторые сильнодействующие адаптации в сеть родителя, которая позволяет Генетическому Алгоритму исчезнуть от любых местных минимумов. Качество мутантной сети есть тем самым, только повторной важности. Мы выбрали для вида действия вращение. Для начала, центр тяжести всех узлов высчитан и узлы сети заказаны (в дуговом пути) согласно их полярной ситуации от центра тяжести. Связи в мутантной сетью тогда получают с помощью вращения узла, нумерующего свыше одно местоположение и перечерчивающего связи сети родителя между теми же номерами узла в мутантной сети. Это иллюстрировано в рисунке 3 на проблеме 8-узла.

Сети родителя, которые будут использоваться для действия мутации, случайно избраны. Обычно мутантные хромосомы в форме популяции - только малая частица общей численности популяции.

Генетический Алгоритм, описанный выше, предоставляет возможность нам исследовать область поиска ACSND в совершенном и эффективном пути, но недостатки некоторых сильных директив по направлению к связи со связностью созданной топологии 2. Например, связь-связность сетей детей, созданных с действием crossover, часто ниже, чем 2. Таким образом, в контрасте со стандартной Генетической парадигмой Алгоритма, некоторые шаблоны директив были введены, чтобы оптимизировать хромосомы индивидуально (посмотрите на рисунок 1). Самыми важными шаблонами оптимизации являются:

1. С одной стороны, чтобы гарантировать связь со связностью как минимум 2, каждый узел сети должен иметь как минимум степень 2. Отныне, связи будут добавлены, чтобы связать соседние узлы с низкой степенью. С другой стороны очень высокие степени узла обычно приводят к высоким затратам сети, так что (долго) связи между двумя узлами с высшей степенью узла могут исключаться.

2. Топология, содержащая связи, которые пересекают друг друга обычно приводит к более высокой стоимости сети, чем топология без возражения связей, без обеспечения добавочной связности. Отныне, две связи возражения пренебрежены и заменены невозражающими связями (если эти связи не присутствуют еще).

3. Если затраты (c2) системы линии высоки по сравнению с кабельной стоимостью (c1), вводя дополнительные связи в сеть со связью-связность 2 может уменьшить полную стоимость сети (благодаря более коротким путям послания).

4. После вычисления матрицы связи-связность топологии, связи могут добавляться между узлами с взаимной связностью ниже 2. С другой стороны, длинные связи, которые связывают узлы с очень высокой взаимной связностью, могут исключаться, чтобы уменьшить стоимость сети. Если нужно, этот процесс оценивания связности сети и добавления/исключающего некоторых связей может повторяться.

Шаблоны 1, 2 и 3 являются скорее довольно грубыми, чтобы исправить некоторые главные недостатки хромосомы быстро, пока шаблон 4 - это очищенный метод, используя больше времени CPU. Влияние этих 4 шаблонов на качество заключительного решения было проверено пространственно и оказалось существенным. Важность включения методов проблемной специфики в Генетическом Алгоритме, чтобы увеличить поисковую эффективность также наблюдалась для широкого ряда других проблем оптимизации (Michalewicz, 1997).

Некоторые типичные значения для самых важных Генетических параметров Алгоритма показаны в таблице 1. Вообще, алгоритм, оказывается, очень крепок и не очень чувствителен к точным значениям параметра, так что прекрасная настройка значений не очень полезна.

3. Запасная Емкостная Локализация (SCA)

Алгоритм SCA начинается от исправленной топологии и исправленного назначения трудоспособности. Задача - локализовать достаточную запасную вместимость, чтобы позволить полную реставрацию связи единых отказов минимальной стоимостью (использование одного модуля m, например m = 16, если мы используем системы волокна STM-16). Кроме того, подходит для использования во Включенном подходе (посмотрите Секцию 4), алгоритм должен быть способен обеспечить скорее хорошие решения быстро и очень хорошие решения в течение длинного движения.

Алгоритм состоит из трех фаз: минимальная запасная емкостная процедура локализации, грубое запасное емкостное дополнение и фаза сжимания (посмотрите рисунок 4).

3.1. Фаза 1: минимальная запасная емкостная локализация

Начиная от рабочей трудоспособности на каждой связи, простой и чрезвычайно быстрый метод может использоваться, чтобы назначить некоторую начальную запасную вместимость на связях. Действительно, если отдельные связи l1, l2, …li формируют цепь, 4 запасной емкости на lx связи должны быть как минимум такими же большими как w(ly) трудоспособности на любом другом ly связи цепи (благодаря принципу реставрации связи).

3.2. Фаза 3: ёмкостное сжимание

Эта последняя и самая поглощающая по времени фаза начинается от решения, найденного во второй фазе, и пробует удалить некоторые m-единицы запасной вместимости со связей. Мы повторно ищем связь (или одну из связей) с самыми чрезмерными единицами запасной вместимости, с помощью изменения образцов перенаправления таким образом, что считаемая связь избегается как можно больше, пока почитание запасных емкостных ограничений есть на остальные связи. Мы тогда удалили одну m-единицу запасной вместимости со связи с самыми чрезмерными единицами. Эта процедура повторяется, пока никакие чрезмерные m-единицы запасной вместимости не оставлены. Философия после исключения только одной m-единицы на связи во времени вместо исключения как много m-единиц как возможно основан на интуитивном мнении, что, с помощью действия за менее жадной модой, заключительный результат будет в общем показан в более подробном описании запасных ресурсов через сеть, приведение к более эффективному совместному использованию запасных ресурсов.

Чтобы развивать скорость фазы сжатия, мы позволяем грубый, приближенный поиск связи с самыми чрезмерными запасными единицами. Например, для того, чтобы решить от кого связать m-единицу запасной вместимости должен исключаться, мы можем сравнить связи относительно числа запасных m-единиц или m/2-единиц связи, которые целиком чрезмерны (то степени детализации или m/2 вместо 1). Этот грубый алгоритм SCA намного быстрее и обычно не производит решение качественно важнее.

Замечание: Продолжение алгоритма по направлению к многоразовым типам. Например, давайте предположим, что три способности типа STM-16, STM-4 и STM-1 считаются и что стоимость STM-16 - это дважды стоимость STM-4 и четырежды стоимость STM-1 (экономика принципа масштаба). Затем, с тех пор, как системы волокна STM-16 - это самый эффективный по стоимости вариант (нижайшая стоимость за емкостную единицу), мы сразу выполняем три фазы алгоритма SCA для m = 16, приведение к емкостной локализации с системами линии STM-16. Затем фаза сжатия 3 выполняется опять, чтобы заменить некоторые системы STM-16 системами STM-4 и/или STM-1, с помощью приспособления образца сжатия, если необходимо. С тех пор, как удаление STM-16 одним STM-1 обеспечивает сейчас высочайшее сохранение стоимости за исключенную емкостную единицу, мы начинаем с повторного поиска связи с 15 чрезмерными единицами вместимости и замены одного из STM-16 на этой связи STM-1, приведение к экономии затрат соответствующих 0.75 STM-16. Если никакие связи с 15 чрезмерными единицами не оставлены, мы повторно ищем связи с 12 чрезмерными единицами (замена STM-16 – на STM-4, экономия затрат 0.5 STM-16) и окончательно мы связываемся связью с избыточностью 11 (замена STM-16 на STM-4 и STM-1, экономия затрат 0.25 STM-16). Должно подчеркиваться, что это продолжение мульти способности алгоритма SCA - это не простая оптимизация связи решения единой пропускной способности STM-16, с тех пор, как адаптация образца сжатия возможна в каждой замене пропускной способности.

4. Включенный алгоритм резкого подъема вверх

Последовательный трехфазный подход, чтобы управлять петлевой проблемой (определение в Секции 1) проекта сети SDH восстановления кажется естественным. Один мог бы начать с проектирования подходящей топологии связи, соединяя все узлы, пока удовлетворение определенных принуждений связности, чтобы гарантировать некоторую надежность (посмотрите для примера Monma и Shallcross (1989)). Один раз топология исправлена, кто-то мог бы разработать образец послания и назначить достаточную пропускную способность на каждой связи. В третьей фазе, кто-то начинает с данной топологии и пропускная способность назначения, чтобы высчитать нужную запасную вместимость на связях для гарантирования полного восстановления связи единых отказов системы (посмотрите например Grover, Bilodeau, и Venables (1991)). Преимущество такого последовательного подхода - это скорость вычисления: с помощью деления полной проблемы проекта в трех подпроблемах, которые решены независимо, заключительное решение найдено относительно быстро (или, начатое другим способом, мы можем разработать большие сети SDH в пределах разумного времени вычисления). Однако взаимная связь трех подпроблем безнадзорна, например выбор топологии имеет влияние на емкостные затраты и послание работающего трафика имеет определенное столкновение на запасной емкостной стоимости. Как последствие, отделение трех подпроблем может привести к низким качественным решениям (т.е., высоким затратам).

Чтобы преодолеть этот недостаток, кто-то мог бы попытаться удержать проблему проекта как целое: отношения между тремя подпроблемами, описанными выше, полностью взяты к рассмотрению. Такой интегрированный подход делает возможным создание решений высокого качества. Однако, требуемые ресурсы, время вычисления и требования памяти, обычно намного выше, чем для последовательного подхода. Как последствие, только меньшие проблемные примера могут решаться на практике. Чтобы разработать большие сети, упрощающие предположения или преждевременное окончание алгоритма, он должен применяться, чтобы уменьшить время вычисления и/или требования памяти. Эти меры однако воздействуют на качество решения.

Проблемы, сталкивающиеся с этими двумя основными различными подходами, дают начало новому подходу, который формирует компромисс между последовательным и интегрированным подход: Включенная стратегия поднятия вверх. Философия 'zooming-in' применена относительно как точность решения, так и поисковое усилие. В первой стадии (s) алгоритма грубое решение конструируется, основанное на упрощении предположений. Как доходы алгоритма, более точные модели используются и поисковое усилие увеличено. Конечная стадия алгоритма берет все проблемные детали в счет и выполняет совершенный и подробно описанный поиск.

Включенная стратегия резкого подъема вверх также отображается в эволюции оборудования оптимизации, которое используется в алгоритме. Всемирные конструкции сжатия используемые в начале, в конечном счете объединят с некоторыми случайными элементами, чтобы получить более всемирный вид пространства решения. Впоследствии, перемещения ударения по направлению к местному оборудованию улучшения, где припода поиска становится больше определяющей.

Включенный подход пробует объединить преимущества как последовательного подхода в вычислениях скорости, так и интегрированного решения высокого качества. Чтобы достичь этого, осторожный выбор должен быть сделан к проблеме деталей, которые считаются в каждой фазе алгоритма. Это решение обычно основано в запрете на торговлю: счет дополнительного аспекта проблемы улучшает качество решения, но и руководства к приросту требуемого времени и памяти.

Дополнительное преимущество Включенной стратегии - это гибкость. В зависимости от времени или доступной памяти, некоторыми проблемными деталями можно пренебрегать во время одной или более фаз. С одной стороны, для малых проблемных примеров, мы можем объединить большое число проблемных деталей от начала алгоритма, приведение к решениям высокого качества. С другой стороны, Включенный подход также полезен для намного больших проблемных примеров, с тех пор, как мы можем пренебречь некоторыми проблемными деталями в первых фазах алгоритма, чтобы ограничить время вычисления без утраты слишком многого на качестве решения.

Чтобы обратить Включенную стратегию к проблеме проекта сети SDH, взаимодействия между проектом топологии, назначение пропускной способности и запасное емкостное назначение должны изучаться старательно. Мы окончательно выбрали для четыре-фазового алгоритма (посмотрите таблицу 2).

5. Выводы

Алгоритм разработан для наиболее оптимального проекта петлевых сетей восстановления SDH. Техника основана на отдельных блоках построения, как например вид Генетического Алгоритма, чтобы разработать начальную топологию, процедуры локальной оптимизации, чтобы приспособить топологию к специфической емкостной процедуре назначения и алгоритму SCA, чтобы назначить запасную вместимость для гарантирования полный восстановления связи единых отказов системы. Чтобы объединить эти блоки построения в полном методе, Включенная стратегия резкого подъема вверх применена: алгоритм постепенно перемещается от грубого решения, основанного на приближенном описании проблемы по направлению к очищенному решению, берущему все проблемные детали в счете. Этот новый подход, который формирует компромисс между последовательным и интегрированный метод, нацелен на объединение преимуществ обоих подходов.

Алгоритм был проверен пространственно на отдельных различных проблемных примерах и результаты были сравнены с другим оборудованием, упомянутым в литературе. Эти эксперименты показывают, что Включенный алгоритм резкого подъема вверх - это совершенно многообещающая техника, которая способна доставить решения высокого качества, используя скромные требования времени и памяти. К тому же, используют подход обеспечивающий гибкий каркас относительно изменения проблемных формулировок: обычно только некоторые незначительные модификации нужны, чтобы попытаться удержать связанные проблемы. Работа изучает введение других восстановительных механизмов и более комплексных сценариев отказа моделирования.

Источники

1. Ahuja, R.K., T.L. Magnanti, и J.L. Orlin. (1993). Течения сети: Теория, Алгоритмы и Приложения. Englewood, Нью-Джерси: Prentice.

2. Gavish, В., Т. Trudeau, m. Dror, m. Gondreau. (1989). Проект Сети Длины окружности "Fiberoptic Согласно с Принуждениями Надежности," Журнал IEEE на Отобранных Областях в Коммуникациях 7(8), 1181-1187.

3. Goldberg, A.V. и R.E. Tarjan. (1988). "Новый Подход к Максимальной Проблеме Течения," Журнал ACM 35, 921-940.