Глава 1. ТЕОРИЯ АСПИРАЦИОННОГО МЕТОДА ПРИ ИДЕАЛЬНЫХ УСЛОВИЯХ.
1.1 ВОЗДУШНЫЕ ИОНЫ
H.F. Tammet
Перевод статьи: Авраменко С. В.
Источник: Х.Ф. Таммет "Аспирационный метод измерения спектра аэроионов", Ученые записки ТГУ, вып. 195, 1967, с 8-13.
Фундаментальные представления о механизме электрической проводимости воздуха были установлены в начале пошлого столетия. Обширный обзор в более ранних трудах возможно найти в известной монографии Видеманна /Wiedemann, 1885/.
Электрическая проводимость воздуха связана с присутствием заряженных частиц, способных к перемещению в электрическом поле. Элементарные ионизационные явления создают положительно заряженные ионы и свободные электроны. Однако, продолжительность жизни свободных электронов и мономолекулярных ионов в воздухе при атмосферном давлении очень коротка. Свободные электроны и мономолекулярные ионы играют ощутимую роль только в самых быстрых процессах, для исследования которых аспирационный метод не подходит по различным причинам. Нейтральные молекулы присоединяются к изначально заряженным частицам, их притяжение обусловлено электрическими и молекулярными силами. Относительно стойкие частицы, образованные таким образом, называются легкими воздушными ионами - аэроинонами. Мало звестено о внутренней структуре легких воздушных ионов /Israel, 1957b/, Сегал /Segal, 1962/ пробовал вычислить теоретически вероятность образования легких воздушных ионов с различными структурами.
Легкие воздушные ионы занимают существенную роль в механизме проводимости атмосферного воздуха.
Вскоре после учреждения ионной теории воздушной проводимости, было обнаружено существование больших носителей заряда / Townsend, 1898;Lenard, 1900; Langevin, 1905a, 1905b/; они были названы тяжелыми воздушными ионами. Тяжелые воздушные ионы сформированы в результате соединения легких воздушных ионов к частицам аэрозоля, содержащимся в воздухе. Первоначально, тяжелые воздушные ионы не являются ионами в обыкновенном смысле, но частицы подвешенные в воздухе остаются стойкими даже после утраты их заряда.
Легкие и тяжелые воздушные ионы перемещаются с различными скоростями в электрическом поле. Для изучения электрических потоков в воздухе, другая природа носителей заряда не имеет никакого значения и это указывает на то, чтобы характеризовать воздушные ионы только их подвижностями. Таким образом целесообразно описать легкие и тяжелые воздушные ионы с общей точки зрения, используя общие понятия.
В сфере атмосферного электричества обычно используют атмосферные ионы, которые имеют такие же характеристики как ионы воздуха. Однако, заряженные частицы, созданные в лаборатории или промышленности также влияют на ионный состав воздуха.
Средняя скорость воздушного иона в электрическом поле пропорциональна напряженности E:
![]() (1.1)
(1.1)
Для более легких воздушных ионов, отношение (1.1) пригодно только в пределах до 10кВ/см /Mitchell, Riedler, 1934; Balog, 1944/.
Подвижность k воздушного иона есть положительным значением для положительно заряженных и негативным для негативно заряженных воздушных ионов. Обычно, абсолютная величина k находится также, как подвижность воздушных ионов. Допустим, что если некоторое множество x имеет подмножество, то
|x| = x. (1.2)
Наибольшие частицы, которые могут считаться воздушными ионами, - это те для которых гравитация и силы инерции все еще незначительна. Достаточное условие для этого следующее:
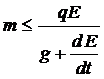 (1.3)
(1.3)
где m - это масса частицы, g - это гравитационная постоянная, и q - это абсолютная величина заряда частицы.
Это описание воздушного иона удовлетворительно, если химическая природа и масса носителей заряда не имеет никакого значения, как при рассмотрении процессов в воздухе. Во многих случаях, однако, химическая природа и масса частиц не может быть не учтенной, и такие проблемы есть в нашем анализе.
Обыкновенные методы измерения предоставляют только макроскопические параметры ионизированного воздуха. Заряды индивидуальных ионов необнаружимы. Таким образом целесообразно характеризовать ионизированный воздух в пределах параметров, которые независимы от зарядов аэроиона.
Ионизированный воздух характеризуется дифференциальной функцией распространения подвижности плотности заряда, или дифференциальным спектром подвижности
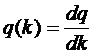 (1.4)
(1.4)
где dq - это плотность заряда за счет воздушных ионов с подвижностью в диапазоне от k до k+dk.
Функция распространения q(k) положительна для положительных k и отрицательна для негативных k. Чаще используют один спектр, который является абсолютными величинами Q(k) и определяется по (1.2).
Он описывает спектр воздушных ионов одной полярности. Чтобы описать спектры воздушных ионов обеих полярностей придется ввести две функции. Спектр подвижности воздушных ионов положительной полярности обозначают p+ (A). Если рассматриваются воздушные ионы только одной полярности, и полярность известна, то индекс пренебрегается.
Плотность заряда в интервале (k1, k2) определена интегралом от функцией распространения
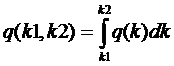 (1.5)
(1.5)
Таким же образом находят плотность негативного заряда q- = q(-?,0), плотность положительного заряда q+=q(0, +?) полная плотность заряда q=q(-?, +?).
Ни спектр проводимости, ни объединенная проводимость q=q(-?, +?) может быть отрицательным. В системе абсолютных величин плотность заряда и проводимость положительны, если k1<k2, иначе - отрицательны. Здесь, и k1 и k2 должены представить подвижность такой же полярности. Чтобы описать спектр воздушных ионов обеих полярностей, мы должны рассматривать два комплекта параметров: q+=q(0, +?), q- = q(-?,0) . Как описывалось выше, индексом + или -, можно пренебрегать или писать в форме ±.
Использование функции (1.4, 1.5) облегчает графическое представление спектра аэроионов в больших интервалах подвижности. Функция g(k) не принадлежит этому интервалу, так как она обычно имеет большие значения в областии малой подвижности, и наоборот. Особое внимание нужно уделить графическому представлению спектра проводимости на логарифмическом масштабе подвижности. Область под кривой g(k) в данном случае пропорциональна к плотности заряда.
Иногда, распространение подвижности воздушных ионов характеризуется частичными сгустками заряда гипотетических дискретных групп. Теоретически этот методов измерения является наиболее точным подходом. Фактическое распространение скорости аэроиона в определенных экспериментальных условиях не строго дискретно (из-за диффузии аэроионов - самый очевидный фактор). Даже если спектр аэроиона окажется дискретен, то он должен начаться с предположения непрерывного распространения при установке и оценивании наблюдений, для того, чтобы доказать дискретность. Это лучший способ вынести объективную информацию. Дискретное распространение может рассматриваться как частный случай непрерывного. Чтобы производить превращение математики от непрерывного к дискретному распространению, нужно все преобразовать к виду:
![]() (1.6)
(1.6)
где Cn - это определенные плотности воздушных ионов с подвижностью q. По свойству полученной функции все целочисленные выражения преобразовывают в суммы, которые характерны для дискретного распространения.
На практике часто пытаются вычислить плотность числа воздушных ионов. Если заряд всех воздушных ионов равняется одному элементарному заряду, то
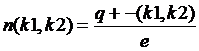 (1.7)
(1.7)
где е - это элементарный заряд.
К сожалению предположение q = e сохраняется только для легких воздушных ионов. Тяжелые воздушные ионы и более тяжелые, искусственно созданные, заряженные частицы аэрозоля, возможно, несут больший заряд. Когда дело обстоит так, формула (1.7) не предоставляет фактическую плотность числа, а только некоторое относительное количество. Если истинный средний заряд воздушных ионов неизвестен, то это было бы более правильным для упоминания о плотности заряда, выраженной в элементарных зарядах на объем единицы вместо плотности числа. Для отдельно заряженных воздушных ионов последнее количество совпадает с плотностью числа воздушных ионов.