Авторы: B G Thomson & A F Kuckes 

Источник: http://www.mech.northwestern.edu/ME224/ME224_Lab_6.pdf

Перевод: Базаров Н.Д.

(This is adapted from ”IBM-PC in the laboratory” by B G Thomson & A F Kuckes, Chapter 7)

 

 1. Введение
Твердое тело, двигающееся через жидкость, обладает силой, воздействующей на него, которая зависит от вида жидкости. Например, намного тяжелее, плавать в меде, чем это находится в воде. Параметр, который описывает эту разницу, - вязкость  (). Сила давления также зависит от других параметров как например внешняя область тела и плотности жидкости. Компьютер будет запрограммирован, чтобы измерять скорость сферы, падающей через глицерин и, чтобы вычислить вязкость. Измерения производятся фото сенсорами.

 

 2. Усилие, необходимое для перемещения твердого тела в жидкости.
В этом разделе будет обсуждаться физика шара, движущегося в жидкости. Есть два различных режима: если сфера движется медленно, доминирует силой, противостоящей её движению за счет вязкости. Для быстрого движения инерционное сопротивление жидкости из-за своей плотности является доминирующим фактором. Величины сопротивления в функциональной зависимости от размеров сферы, скорости, плотности и вязкости жидкости могут быть оценены с трудом в обоих случаях. Действительно, при турбулентных явлений точные вычисления не представлилось возможным

 

(6.1)

 

, где -вязкость жидкости.
Эта проблема поддается точному математическому анализу, который впервые был сделн Стоксом и соотношение известно как закон Стокса для вязкого сопротивления шара, движущегося в жидкости. Его результат:

 

(6.2)

 

закон Стокса экспериментально проверен для случая, когда движение сферы достаточно медленно. Приближенный подход использованый выше, дает важную информацию физического происхождения формулы Стокса.
Более быстрое движение приводит к турбулентнму следу за сферой. Хотя точные математические вычисления силы сопротивления в этом режиме не были сделаны, наблюдается относительно хорошая оценка силы. Чтобы переместить объект быстро, скорость жидкости на пути движения ускоряется с нуля до скорости шара и жидкости оттесняется, а затем формирует турбулентный следа за сферой. В турбулентности, в конце концов рассеивается кинетическая энергия движущейся жидкости, как тепло-и звуковой энергии без какого-либо кинетической энергии обратно в этой сфере. Сила сопротивления сфере будет равна силе, необходимой для оттиска жидкости в сторону.

Оценка массы жидкости переходит в единицу времени, масса столба жидкости увеличивается каждую секунду, пока сфера падает. Это произведение площади поперечного сечения объекта перпендикулярно к направлению движения, на скорость движения V и плотность жидкости. Максимально каждый элемент этого столбца разгоняется до скорости движущегося объекта. Таким образом, работа силы сопротивления на сфере (расстояние силы-х) равна кинетической энергии жидкости (1 / 2  массы движущейся жидкости на v2).

 

Поэтому

(6.3)

 

- это сопротивление на сфере, где А- это площадь поперечного сечения.

Перемещаемоу сопротивление тупому предмету по экспериментально определенному коэффициент лобового сопротивления Cd, по определению:

(6.4)

 

Сочетание pfv2 / 2 называется кинетическое давление жидкости. Экспериментально определенный коэффициент сопротивления шара, движущегося быстро через жидкость Cd = 0,5.

Объединяя соотношения Стокса с турбулентными силами получим полную силу сопротивления на падающем объекте

 

(6.5)

 

Как показывает уравнение (6.4) , турбулентное сопротивления для шара пропорционально квадрату скорости, поэтому является основным явлением на высокой скорости в то время как вязкое сопротивления является более важным для медленно движущейся сферы.

Коэффициент турбулентной силы сопротивления для сферы в вязкой среде:

 

(6.6)

(6.7)

 

Параметр Re (безразмерный) называется числом Рейнольдса, она используется в качестве меры турбулентности потока жидкости. Длина (2r), используемая в определении Re для данного тела, как правило, принимаются, как длина хорды в направлении движения. Таким образом, для сферы это диаметр.

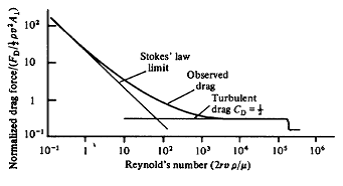
Настройка Уравнения (6), равного 1, показывает, что переход от гладкой к турбулентному происходит при числах Рейнольдса около 48 (с CD = 0,5). Рисунок 6.1 показывает  график силы сопротивления против числа Рейнольдса в диапазоне чисел Рейнольдса от 10 до 106и показывает, что переход происходит в широком диапазоне чисел Рейнольдса. Плавный режим течения, как правило, ниже числа Рейнольдса 1 и турбулентный режим выше 103.

                             

Рисунок  1.

    

Сфера, начиная от осциляции в жидкости будет под действием гравитации Fg и силы плавучести Fh. Как только оно начинает двигаться, сила сопротивления будет выступать Fd чтобы замедлить её ускорение. По законам Ньютона

 

(6.8)

 

Fg и Fb постоянны несмотря на скорость шара но Fd зависим от скорости. Если предполагается течение стоксовское , то выражение (6.7) становится отличительным выражением для скорости сферы

 

(6.9)

 

3. Экспериментальная установка

Для измерения вязкости жидкости используется прибор, показанный на рисунке 2. Она состоит из столба глицерина в котором могут быть пропущены сферы различных размеров и составов для наблюдения падение под действием силы тяжести. Скорость падающего шара может быть измерена, отметив, момент, когда он проходит через каждый из 4 световых пучков.

 

Рисунок  2.

 

Каждый из четырех лучей света, пересекаются в колонке глицерина. Светодиодный источник света активирует фото сульфида кадмия-резистор, сопротивление которого меняется, когда свет падает на него. Изменение сопротивления необходимо преобразовать в цифровой сигнал, пригодный для компьютерной обработки данных.

LED - маленькая выдерживающая высокие нагрузки лампа, которая требует около 10 mA потока и 1.5 V,для работы.

Фото-резисторы сульфида кадмия используются во многих камерах, чтобы вычислить время экспозиции. Как термистор, это пассивное устройство, с изменяемым сопротивлением. Датчик сульфида кадмия имеет сопротивление более 20 МОм в темноте, и сопротивление в сотни Ом при ярком солнечном свете, так что его сопротивление изменяется на более чем 100 000 до 1. Хотя это и весьма большая чувствительность к свету, ячейки сульфида кадмия довольно медленное устройство, около 30 мс в полной мере отвечает на внезапное изменение уровня освещенности.

Чтобы перевести изменение сопротивления, индуцируемого в фото резисторе в цифровой сигнал, напряжение компаратора используется (рис. 3).

 

Рисунок  3.

 

Компаратор будет производить вывод либо 5 В или 0 V в зависимости от того, чтобы входное напряжение + вход прибора больше или меньше, чем напряжение - ввод. Каждый LM339 имеет четыре таких компараторов в одном 8 * 15 мм кристалле интегральной схемы. Компаратора схемы на рис 3 имеет положительную обратную связь; это занимает больше напряжения, чтобы включить его и меньше напряжения, чтобы отключить его, чем изменения напряжения, необходимые для обеспечения компаратора выключателем. Этот гистерезис аналогичный тому, который используется в регуляторе температур. Схема называется триггер Шмидта и часто используется с механическими переключателями для ликвидации дребезга.

Единственная экспериментальные проблема с этим аппаратом состоит в том, что при большом диаметре шаров, стены колонки взаимодействуют с потоком и влияют на движение шара.

Значения вязкости при этом можно исправить с помощью эмпирической формулы (Dinsdale & Moore, вязкость и ее измерение, Reinhold Publishing, New York, 1962):

 

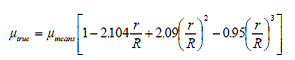
где R - радиус колонки и r радиус шара.