Возможности использования обыкновенных дифференциальных уравнений при изучении реальных явлений и процессов очень велики. Рассмотрим один из примеров использования дифференциальных уравнений для выбора правильной стратегии при решении задач поиска.

Пусть, например, миноносец охотится за подводной лодкой в густом тумане. В какой-то момент времени туман поднимается и подводная лодка оказывается обнаружена на поверхности воды на расстоянии 3 миль от миноносца. Скорость миноносца вдвое больше скорости подводной лодки. Определим траекторию, по которой должен следовать миноносец, чтобы он прошел точно над подводной лодкой, если она сразу же погрузилась после ее обнаружения и ушла на полной скорости прямым курсом в неизвестном направлении.

Пусть полюс находится в точке обнаружения подводной лодки, а полярная ось r проходит через точку, в которой в момент обнаружения подводной лодки был миноносец.

Прежде всего, миноносцу надо занять такую позицию, чтобы он и подводная лодка находились на одном расстоянии от полюса. Затем миноносец должен двигаться вокруг полюса по такой траектории, чтобы оба движущихся объекта все время находились на одинаковом расстоянии от точки О. Только в этом случае миноносец, обходя вокруг полюса О, пройдет над подводной лодкой. Таким образом, сначала миноносец должен идти прямым курсом к точке О до тех пор, пока он не окажется на том же расстоянии X от полюса О, что и подводная лодка. Тогда расстояние можно найти из уравнения:

либо из уравнения

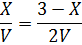
где где V- скорость подводной лодки; 2V- скорость миноносца.

Если "встречи" не произошло, то миноносец должен в дальнейшем двигаться вокруг полюса О, удаляясь от него со скоростью подводной лодки V. Разложим скорость миноносца на две составляющие: радиальную 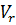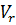и тангенциальную .

Радиальная составляющая - это скорость, с которой миноносец удаляется от полюса, т.е.

Тангенциальная составляющая — это линейная скорость вращения миноносца вокруг полюса. Она равна произведению угловой скорости на радиус, т. е.

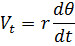
Но так как , то

Таким образом, получаем систему дифференциальных уравнений

Откуда

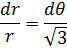
где С - произвольная константа.

Учитывая теперь, что миноносец начинает движение вокруг полюса О с полярной оси r на расстоянии X миль от точки О, то есть учитывая, что r= 1 при θ=0 и r= 3 при θ=-π, тогда С=1 и С=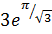

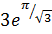
Таким образом, чтобы выполнить свою задачу, миноносец должен пройти 2 или 6 миль прямым курсом по направлению к месту обнаружения подводной лодки, а затем двигаться либо по спирали

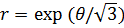
либо по спирали