МЕТОДЫ НАСТРОЙКИ
НЕЧЕТКОГО АДАПТИВНОГО ПИД-РЕГУЛЯТОРА

Михайленко В.С., Ложечников В.Ф.

Источник: http://www.nbuv.gov.ua/../09mvsmtu.pdf

Описание: разработана нечеткая экспертная система, определяющая оптимальные настройки ПИД-регуляторадля, для его адаптации к объекту управления, и ее апробация в пакете Matlab (Simulink)

При управлении сложными объектами, функционирующими в условиях нестационарности, широкое применение нашли адаптивные регуляторы, реализующие типовые ПИ- или ПИД-законы регулирования. Адаптивные контроллеры зарубежных и отечественных производителей: Ремиконт, Овен, Сименс, Микрол и т.д., как правило, реализуют метод Зиглера-Николса [1]. Следует отметить, что данный метод предполагает вывод объекта в область автоколебаний, за счет перехода на П-закон и грубого варьирования коэффициента усиления К_р. Однако, значительный ряд технологических процессов по условиям эксплуатации не допускают автоколебательного режима. Таким образом, задача нахождения оптимального метода адаптации остается открытой.

Вместе с тем, в последнее время широкую популярность находят нечеткие модели и алгоритмы управления [2,3,5]. Известно, что нечеткое управление основано на использовании не столько аналитических или теоретических моделей, сколько на практическом применении знаний квалифицированных специалистов, представленных в форме лингвистических баз правил. Нечеткое управление эффективно в случаях недетерминированности параметров объектов, когда существует определенный опыт экспертов по управлению и настройке автоматизированной системы регулирования (АСР). Теория нечеткой логики позволяет использовать знания специалистов — наладчиков с целью улучшения процессов управления и оказания помощи (супервизорный режим) по настройке типовых регуляторов. Исходя из вышесказанного, задача создания метода адаптации ПИД-регулятора, реализующего опыт наладчиков, становится актуальной.

Целью статьи является разработка нечеткой экспертной системы, определяющей оптимальные настройки ПИД-регулятора, для его адаптации к объекту управления, и ее апробация в пакете Matlab (Simulink). Разобьем научную задачу на ряд этапов. На первом этапе определим структуру адаптивной АСР (рис.1):

Рисунок 1 — Структура адаптивного нечеткого управления

где Е — ошибка; Z — задание; Y — выходное значение; N — возмущение; Кр, Ти, Кd — настройки ПИД-регулятора.

На втором этапе в программе Matlab (FLT) производится создание системы нечет-
кого вывода или адаптера (рис.2)

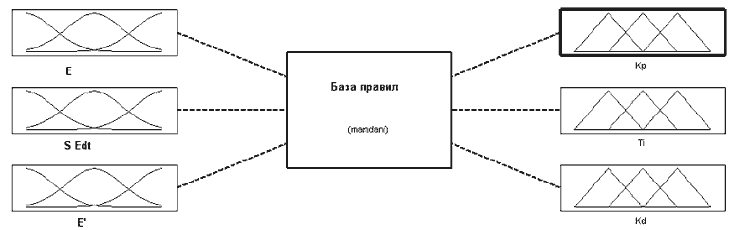
Рисунок 2 — Графический интерфейс редактора FIS

На третьем этапе проводится фаззификация входных и выходных лингвистических переменных (ЛП). Фаззификация входных значений (ошибки регулирования (Е), ее интеграла и производной) производится согласно рекомендациям [4]. Графики функций принадлежности входных ЛП представлены на рис. 3 – 5.

Функцию принадлежности Z‑вида, представляющую терм – «отрицательная ошибка otr » можно представить в виде: f_z (x, − 0.6, − 0.1) = [ 1, x < − 0.6; − 0.1 – x / 0.5; 0, − 0.1 < x].

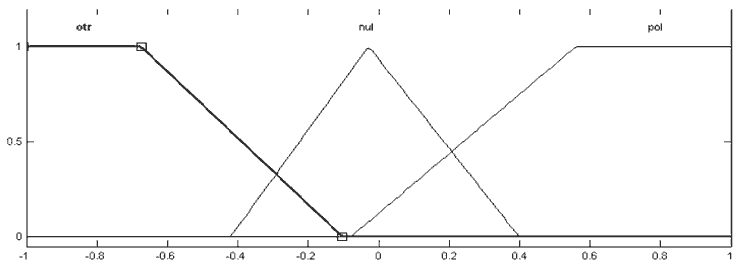
Рисунок 3 — Функции принадлежности ЛП «ошибка»:
оtr — отрицательная, nul — нулевая, pol — положительная

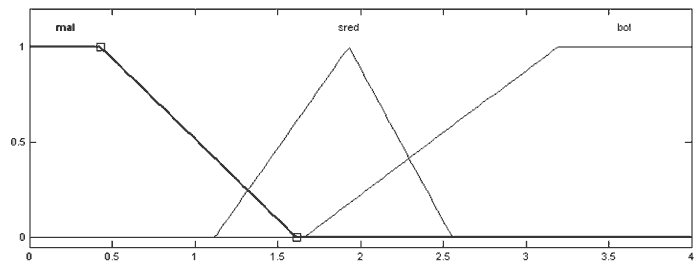
Рисунок 4 — Функции принадлежности ЛП «интеграл ошибки»:
mal — маленький, sred — средний, bol — большой

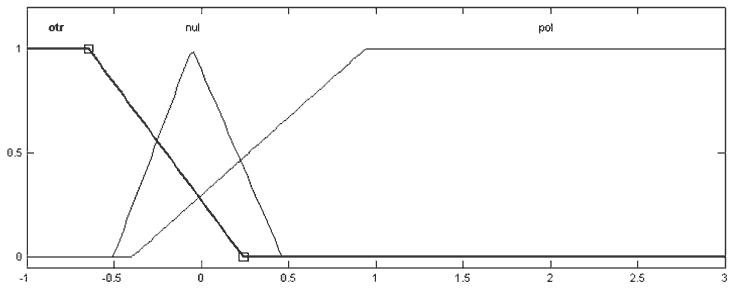
Рисунок 5 — Функции принадлежности ЛП «производная ошибки»

Этап фаззификации выходных ЛП «настройки ПИД-регулятора» проведен с учетом рекомендаций [4,5] и представлен на рис. 6.

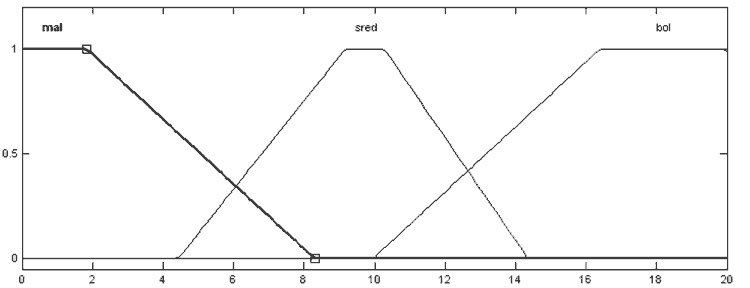
Рисунок 6 — Функции принадлежности ЛП «коэффициент усиления Кр»:
mal — маленький, sred — среднний, bol — большой

Функции принадлежности ЛП «Т_и» и «К_d» также отображаются Z и S – образными графическими видами. Следует отметить, что Ти лежит на универсуме [0-5], а К_d = [0-15]. Четвертый этап заключается в создании базы правил вида «ЕСЛИ …ТО». Исходя из рекомендаций из специализированной литературы [5], проведенных экспериментов в редакторе FLT, а также опыта экспертов-наладчиков систем автоматизации, предлагаются следующие правила: ЕСЛИ «ошибка есть отрицательная» И «интеграл ошибки есть маленький» И «производная ошибки есть отрицательная» ТО «К_р есть большой», «Т_и есть большой», «К_d есть большой» и т.д. (рис. 7)

Рисунок 7 — Фрагмент базы правил

На следующем этапе проводится компьютерное апробирование нечеткой модели. В первоначальном эксперименте использовалась АСР с ПИД-регулятором, функционирующем по каналу задания Z=1, при влиянии на объект канала возмущения при этом: W_об(S) = 2.5/(5S²+3S+1); W_N(S) = 0.5/(5S+1). Настройка регулятора проводилась методом Зиглера-Николса. Значения настроек равны К_р = 1.3; Т_d = 0.15; К_d = 10.3, а переходный процесс удовлетворяет основным показателям качества. Предположим, что в связи с неопределенностью условий эксплуатации объекта, произошло изменение значений ключевых параметров такового. Например, W_об(S) = 2.5/(15S² +2S+1); W_N(S) = 3.5/(15S+1). При известных настройках регулятора, переходный процесс с новыми значениями передаточных функций обладает перерегулированием G = 80%, что недопустимо (рис.8).

Рисунок 8 — Переходный процесс по каналу задания

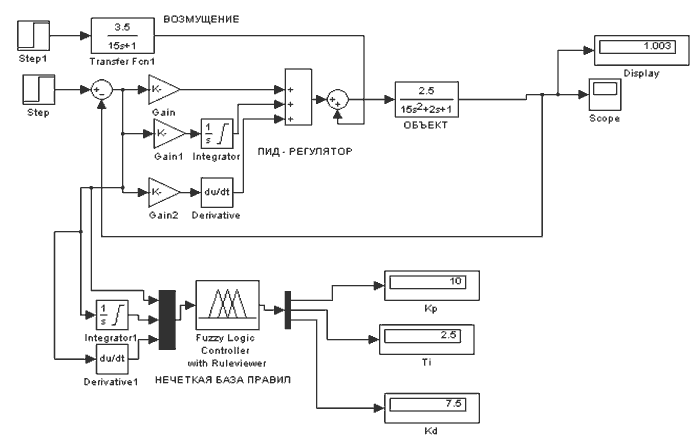
Рисунок 9 — Экспериментальная схема, выполненная в программе (Simulink)

Таким образом, необходима временная остановка сложного технологического процесса и перенастройка значений настроек ПИД-регулятора. Произведем проверку нечеткого адаптера при известных условиях (рис.9). Нечеткая система выдала следующие результаты: К_р = 10; Т_и = 2.5; К_d = 7.5, а переходный процесс регулирования при данных настройках для ПИД-регулятора показан на рис.10.

Рисунок 10— Переходный процесс, полученный при адаптивных настройках

Как видно из рис.10, перерегулирование G не превышает 30%, что допустимо, а время регулирования T_р уменьшилось по сравнению с предыдущем на 30 секунд. Результат работы нечеткого адаптера в программе Matlab (FTL) показан на рис.11.

Рисунок 11 — Результат работы нечеткого адаптера

Таким образом, использование нечетких адаптивных ПИД-регуляторов позволит эффективно управлять технологическими процессами без их остановов, а дальнейшее введение нейрокомпьютера может привести к самообучающейся адаптации по определению оптимальных настроек без корректировки базы правил.

ЛИТЕРАТУРА

1. Дьяконов В.П. Simulink 5/6/7 Самоучитель.— М.:ДМК, 2008 — 781с.

2. Леоненков А. Ю. Нечеткое моделирование в среде Matlab и fuzzyTech. — С. — Птб.: БХВ, 2003. — 720 с.

3. Мелихов А.Н. и др. Ситуационные советующие системы с нечеткой логикой. — М.: Наука, 1990. — 272 с.

4. Ротач В.Я., Клюев А.С. Автоматизация настройки систем управления. М.: Энергоиздат, 1984 — 272 с.

5. Алиев Р.А., Церковный А.Э., Мамедова Г.А. Управление производством при нечеткой исходной информации. М.: Энергоиздат. 1991. — 234 с.