Використовування алгоритмів теорії самоорганізації в інформаційно-вимірювальних системах
Головіна А.К.,Тарасюк В.П.
Донецький національний технічний університет
Источник: Наукові праці Донецького національного технічного університету. Серія: “Обчислювальна техніка та автоматизація”. Випуск 15(130). — Донецьк: ДонНТУ, 2008. — С.201–207.
Abstract
TarasukV.P., Golovina А.К. Use of algorithms of theory of organization in informatively the measuring systems. It is shown that in the conditions of limited a priori information the synthesis of the informatively-measuring system can be based on two stages: constructing potential useful signs and organization of models. Practical results confirmative efficiency of the use of algorithms of theory of organization at the decision of the intricate applied problems are resulted.
Введення. Останнім часом світовий ринок пред'являє підвищені вимоги до якості продукції, що випускається, до оптимізації протікання технологічних процесів для скорочення економічних, сировинних і інших витрат. Для відповідності підвищеним вимогам сучасних стандартів необхідно робити упор не тільки на якість вихідного продукту, але і на якість технологічного процесу. Цю проблему вирішують, упроваджуючи інформаційно-вимірювальні системи супроводу технологічних процесів. Синтез сучасних інформаційно-вимірювальних систем (ІВС) різного ступеня складності так чи інакше потребує використовування методів і алгоритмів побудови залежностей за експериментальними даними.
Запропонований А.Г. Івахненко індуктивний метод самоорганізації моделей складних систем (метод МГОА) достатньо детально описаний в роботах [1-4]. Тому виникає проблема аналізу ролі і місця алгоритмів самоорганізації МГОА в задачі синтезу інформаційних технологій обробки інформаційно - вимірювальних сигналів, поглянувши на ці алгоритми з боку споживача. Тобто, проаналізувати один з варіантів «зовнішнього критерію» з погляду отримання найзручнішого математичного апарату ідентифікації складних ІВС.
Принцип самоорганізації полягає у тому, що при поступовому ускладненні моделей деякі критерії (властивості «зовнішнього доповнення») проходять через свій мінімум. ЕОМ за допомогою перебору моделей знаходить цей мінімум і указує єдину модель оптимальної складності.
Величину мінімального значення критерію - глибину мінімуму можна розглядати як оцінку якості моделювання і надійності моделі. Якщо глобальний мінімум не досягнутий, значить, модель не знайдена. Це може мати місце в наступних випадках: вхідні дані дуже зашумлени; не містять істотних змінних, або об'єкт є індетермінірованним; опорна функція не підходить для даного процесу; враховується дуже мало аргументів, що запізнюються, і т.п. В таких випадках необхідно розширити область перебору моделі.
Аналіз публікацій і розробок по темі. Існуючі дослідження синтезу математичних моделей ідентифікації ІВС не враховують той момент, що вибір довжини передісторії, що враховується, функціонально не пов'язаний з вибором кроку дискретизації змінних в часі. Ця величина повинна вибиратися з урахуванням поглиблення мінімуму критерію.
Згідно теоремі неповноти Геделя - задача ідентифікації структури і параметрів моделі некоректна: тільки за наявності деякого зовнішнього доповнення можна отримати єдине її рішення. У всіх роботах по моделюванню, де тим або іншим способом отримана єдина модель, застосоване деяке зовнішнє доповнення.
Ця проблема відноситься до проблеми узагальнення і розвитку теорії оптимальних і адаптивних гібридних систем автоматизації ТП, зокрема синтезу ІВС на базі уніфікованих алгоритмів і методів інтелектуального дистанційного керування і збору даних. Ці проблеми відображені в роботах К.П.Власова В.К.Кипа, А.Ф.Кравчука, А.В.Паніна, Е.Е.Рафалеса-Ламарки, В.І.Саліги, В.С.Синепольського, В.О.Ульшина, Д.А.Зубова, Н.А.Шмачкова, J.R.Brigtman, T.S.Brown, S.Cierpisz, і ін. У роботах показано, що основний недолік сучасного моделювання полягає у тому, що зовнішнє доповнення вибирається неадекватно задачі, без урахування погрішності і точність безпосередніх вимірювань.
Постановка задач досліджень. Метою даної статті є аналіз можливості використовування алгоритмів МГОА при синтезі інформаційно-вимірювальних систем, а саме в прикладних інформаційних технологіях (ІТ) обробки сигналів різної фізичної природи і на прикладах рішення практичних задач показати достоїнства даного методу.
Основний матеріал і результати роботи. Розглянемо задачу синтезу ІТ обробки сигналу. Під інформаційною технологією розумітимемо [5] сукупність методів і засобів, об'єднаних в технологічний ланцюжок, на вхід якої поступають початкові дані (сировина), а на виході утворюється інформаційний продукт, підготовлений відповідно до потреб конкретних користувачів в тій або іншій наочній області (див. рис. 1).
Рис. 1 – Загальна схема інформаційної технології
Індуктивний метод моделювання, який засновано на принципі самоорганізації, виходить з мінімального об'єму апріорної інформації, що вимагається для моделювання. Бракуючи відомості ЕОМ знаходить за допомогою перебору (послідовної оцінки) великого числа варіантів моделей по деяких зовнішніх критеріях. Таким чином, практично метод є комбінованим: використовується достовірна апріорна інформація про об'єкт і індуктивний перебір і оцінка моделей-претендентів. Оцінки знаходяться по порівняно невеликій частині початкових досвідчених даних. Решта даних використовується для отримання оцінок коефіцієнтів і з'ясування оптимальної структури моделі.
Розглянемо наступну задачу. Є деякий технічний або технологічний об'єкт, про стан Z якого необхідно одержати кількісну або якісну інформацію (див.рис. 2).
Рис. 2 – Опис стану об'єкту
У першому випадку користувача цікавлять значення інтервальних змінних - компонент вектора, а в другому – значення категоріальної змінної, що характеризує приналежність поточного стану об'єкту до одного з класів заданої множини V={V1..Vm}
Існують різновиди задач, коли визначення параметра Z не представляє особливої праці: є достатньо надійні засоби вимірювання (датчики і індикатори), які дозволяють безпосередньо одержати інформацію, що цікавить користувача, про стан об'єкту. Проте досить часто на практиці зустрічаються задачі, коли безпосереднє визначення Z неможливе. Наприклад, агресивність і висока температура середовища перешкоджає створенню датчиків для безпосереднього визначення змісту вуглецю і інших легуючих елементів в розплавленому металі [7]. Неможливо також визначити в'язкість напіврідкої кондитерської суміші експрес-вимірюванням в потоці через не стандартний набір властивостей реологій, що характеризують цю суміш [9].
Аналогічні приклади достатньо часто зустрічаються в хімії, медицині і інших областях науки і техніки. Рішення подібних задач є головною метою ІТ для непрямого контролю параметрів і діагностики стану об'єкту.
Розглянемо яку робочу гіпотезу можна покласти в основу синтезу таких технологій. Припустимо, що при фіксованому значенні Z на виході об'єкту породжується нестаціонарне скалярне або векторне поле (електричне, магнітне, температурне і т.п.). Вважатимемо, що величина цього поля визначається функцією:
y = Ω(x, t, Z). (1)
Яка залежить від параметра Z, де t - час, x - точка простору, у - величина поля в цій крапці. При вимірюванні поля (1) у фіксованій крапці u = u0 функція Ω(x, t, Z) вироджується у функцію часу y(t) = Ω(x0, t, Z). Якщо ж датчики для вимірювання поля (1) встановити в декількох крапках, то (1) можна представити сукупністю функцій часу:
(2)
що є сигналами на виході датчиків.
Для зручності можна записувати (2) у вигляді одного співвідношення:
y(t) = Θ(t, Z); (3)
розуміючи під y скалярну функцію часу, якщо сигнал вимірюється в одній крапці, або вектор-функцію, якщо вимірювання поля виробляється в декількох крапках.
Оскільки передбачається, що сигнал (3) залежить від стану Z, то з формальної точки зору інформаційна обробка ІВС повинна забезпечувати рішення зворотної задачі: вимагається оцінити невідоме значення Z за наслідками спостереження сигналу на фіксованому відрізку спостереження t1≤t≤t2. Схемно це відображено на рисунку 3.
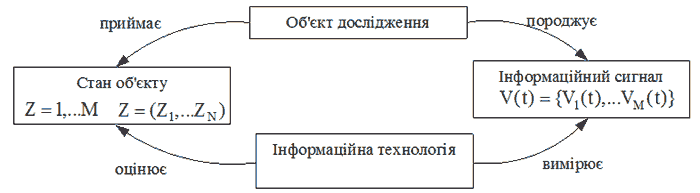
Рис. 3 – Застосування інформаційної технології для обробки вимірюваного сигналу
На практиці, в реальних технологічних системах функція Θ(t) найчастіше невідома. Розробляючи ІТ у складі ІВС доводиться стикатися з достатньо складними об'єктами і процесами, а знання в даній наочній області слабо структуровані і формалізації піддаються лише окремі фрагменти загальної постановки [6]. Для спрощення вивчення фізичних закономірностей часто розглядають умови, що "ідеалізуються", внаслідок чого одержані у такий спосіб моделі приводить до значних погрішностей.
І хоча є всі підстави вважати, що модель вигляду (1) існує, її отримання тільки на ос-нові фізичних уявлень скрутне, а іноді і просто неможливо.
Так, наприклад, відомо, що температура, процентне співвідношення компонентів по-чаткової сировини, час приготування кондитерської суміші, несуть інформацію про якість кондитерської суміші [7], що готується, проте донині не одержані моделі, що адекватно опи-сують процес перетворень реологій жирової складової в результаті розкладання на молеку-лярному рівні, що приводить до зниження якості продукції.
Законами фізики доведено, що температурне поле, утворюване всередині і навколо злитка металу, що кристалізується, несе інформацію про його механічні властивості і хіміч-ний склад. В той же час, згідно [9], процес кристалізації є щонайтіснішим переплетенням фі-зико-хімічних (зародження і зростання кристалів, дифузія елементів, коагуляція домішок), гідродинамічних (рух розплаву усередині злитка) і теплових явищ. Складність цих процесів перешкоджає побудові моделі вигляду (1), адекватно тієї, що описує формування температу-рного поля в процесі кристалізації.
Перелік подібних прикладом можна було б продовжити. Тому модель (1) можна розг-лядати лише як робочу гіпотезу, що дозволяє обґрунтувати принципову можливість оцінки параметра стану об'єкту по спостережуваних сигналах.
Таким чином, до задачі синтезу ІТ обробки сигналів на сучасному етапі розвитку нау-ки слід підходити не стільки з позицій математичної проблеми, що вимагає формального до-зволу, а як до наукової технології рішення конкретних задач. Алгоритми самоорганізації МГОА, орієнтовані на структурну і параметричну ідентифікацію моделей за експеримента-льними даними, є одним з елементів таких технологій. Головною гідністю алгоритмів МГОА, відрізняючи їх від інших методів ідентифікації, є розділення наявних спостережень на дві вибірки: повчальну, по якій виробляється ідентифікація моделей заданого класу струк-тур, і контрольну, що забезпечує селекцію моделей оптимальної складності з погляду деяко-го зовнішнього критерію: регулярності, мінімуму зсуву, балансу змінних і комбінованих. Згідно теоремі Геделя з математичної логіки про необхідність зовнішнього доповнення [4] тільки зовнішні критерії дозволяють вибрати єдину (для кожного критерію) модель оптима-льної складності.
Технологічний процес приготування кондитерської суміші, що розглядається як прик-лад, характеризується часом, що витрачається на виготовлення кожної партії готової продук-ції [10]. Основними технологічними характеристиками дискретно безперервного технологіч-ного процесу є продуктивність і якість виготовлення виробів. На них впливає багато чинни-ків, найважливішими з яких є технологія виробництва, зміна фізіко – механічних властивос-тей сировини та ін.
Процес контролю якості продукції передбачає наступні операції: вибірку проби з по-току; вимірювання показника і експертну оцінку якості готової продукції; ухвалення рішень про внесення коректив в технологічний процес, тобто формування і здійснення управляючої дії. Оскільки якість готової продукції і відповідно точність технологічного процесу визнача-ють його технічні показники, то необхідно розглянути характеристики показника якості го-тової продукції.
Зміна показника якості характеризується серією послідовних випадкових величин Zj(n) (де n – кількість складових у вибірці з деякого моменту часу t0, j – показник якості го-тової продукції). Рівняння для визначення показника якості j=1 можна представити у вигляді суми двох некорельованих послідовностей [1]:
Z(n) = Z1(n)+N(n), (4)
де Z1(n) - детермінована складова показника якості;N(n) - випадкова складова показника якості.
Поява детермінованої складової може бути слідством закономірної зміни технологіч-них параметрів процесу. Оскільки показник якості є випадковою величиною, то в загальному випадку можна розглядати закон розподілу цієї випадкової величини. На рисунку 4 приведені криві, характеризуючи диференціальні закони розподілу показника якості готових виробів некерованого технологічного процесу fZ(Z) і керованого fY(Y) (крива 2).
Рис. 4 – Диференціальні закони розподілу показника якості готової продукції
Показник якості точності технологіч-ного процесу за відсутності системи управління процесом:
(5)
за наявності системи управління:
(6)
Закон розподілу випадкової величини – показника якості – є композицією законів розподілу трьох доданків псевдо детермінованої регулярної складової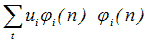 
- відомі функції часу, випадкові величини) і двох випадкових складових S(n) і N(n). Випадкову послідовність S(n) можна розглядати як плавно змінну (низькочастотну) складову випадкової послідовності Z(n), звану корельовано складовою із статичними характеристика-ми:
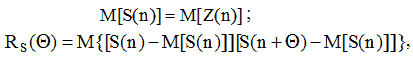(7)
де М – символ математичного очікування, - автокореляційна функція, Θ=1,2,3...
Випадкову послідовність N(n) можна розглядати як високочастотну складову випад-кової послідовності Z(n), звану некорельованою складовою із статичними характеристиками:
(8)
де DN- дисперсія випадкової величини N
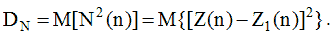(9)
Фізична інтерпретація одержаних результатів вимірювання показника якості для да-ного технологічного процесу полягає в наступному: зміну фізико-механічних властивостей сировини і напівфабрикатів мають випадковий характер, тому залежні від них зміни показ-ника якості готових виробів також мають випадковий характер. Крім того різні партії сиро-вини неоднорідні (причому ця неоднорідність також носить випадковий характер), тому го-това продукція має показники якості, некорельовані між собою. Цим пояснюється поява складової N(n). Усереднені фізико- механічні властивості сировини малих партій змінюються від партії до партії поволі і характеризуються сильним кореляційним зв'язком, що обумовлює появу складової S(n).
За відсутності детермінованої складової і при нормальному законі розподілу регуляр-ної і нерегулярної складових і при математичному очікуванні, рівному деякою постійною, в результаті композиції двох нормальних законів (см.рис. 4, криві 1 і 2) одержуємо нормаль-ний закон розподілу (крива 3) з числовими характеристиками:
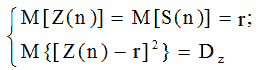(10)
Точність вимірювання вихідного параметра технологічного процесу (показника якос-ті) для цього випадку:
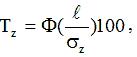(11)
де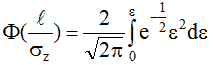 
- інтеграл вірогідності;
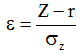- нормована випадкова величина;
- середньоквадратичне відхилення величини Z.
Цільова функція управління тоді формулюється таким чином:
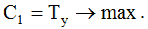(12)
Очевидно, що задача управління полягає в тому, щоб забезпечити точність. У разі, коли розподіл показника якості в межах поля допуску приблизно має нормальний за-кон розподілу, точність керованого процесу відповідно до формули (2) визначається таким чином:
(13)
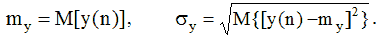(14)
Інтеграл вірогідності є монотонно зростаюча функція, тобто завжди, якщо ε2>ε1. Тоді замість цільової функції (12) можна записати:
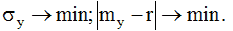(15)
Враховуючи, що 
, то цільову функцію управління (15) з обліком (14) можна записати в наступному вигляді:
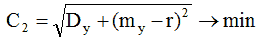(16)
Ця цільова функція управління найбільш зручна при синтезі інформаційної технології для ІВС яка функціонує на основі методів МГОА.
Величина показника якості Z(n) некерованого процесу змінюється в часі випадковим чином, як було показано вище. Перед початком процесу виробляється настройка устаткуван-ня і пристроїв, отже, усереднювання ведеться по безлічі реалізацій випадкової послідовності контрольованого процесу у(n).
У міру випуску виробів (тобто із зростанням n) якість продукції і точність процесу може зменшуватися і при випуску d- й партії готової продукції аналізатор ухвалює рішення про необхідність формування управляючої дії. Причому управляюча дія, сформована за нас-лідками вимірювання d-й партії виробу, може бути використане не раніше, ніж при виготов-ленні (d+1)-й партії. Після цього виробляється контрольна настройка технологічного процесу таким чином, що M[z(d+1)]=r. У разі використовування алгоритмів МГОА цей недолік можно усунути, шляхом введення інформаційної моделі складнішого рівня в перебігу приготування d-й партії виробу.
Звідси витікає, що важливим етапом синтезу ІТ обробки сигналів, передуванням структурно-параметричної ідентифікації об'єкту, є перехід від простору спостережень y(K1)=(y1..yK1)до простору потенційно корисних ознак x(K2)=(x1..xK2), а потім вже етап використовування цих ознак як аргументи моделей непрямого контролю і діагностики, селектіруємих тим або іншим алгоритмом самоорганізації на основі повчальної і контрольної вибірок.
Саме такий погляд на роль алгоритмів МГОА при синтезі прикладних ІТ обробки си-гналів в умовах обмеженої апріорної і бістро змінюється інформації представляється найре-алістичнішим.
Висновок. У статті показано, що реалістичний підхід до використовування алгоритмів самоорганізації в задачі синтезу ІТ обробки сигналів, заснований на двохетапному рішенні задачі. Перший етап передбачає перехід від початкового простору спостережень до обґрунтованого набору потенційно корисних ознак (потенційних регрессоров) на основі наявної апріорної інформації або розумних евристик. В результаті на другому етапі застосування алгоритмів МГОА дозволяє сконструювати моделі оптимальної складності, дозволяючи побічно оцінювати параметри об'єкту і діагностувати його функціональний стан з урахуванням зовнішнього доповнення, яке вибирається адекватно задачі, з урахування погрішності і точності безпосередніх вимірювань.
Література
- Ивахненко А.Г. Индуктивный метод самоорганизации моделей сложных систем. – К.: Наук. думка, 1982. – 360 с.
- Ивахненко А.Г., Мюллер И.А. Самоорганизация прогнозирующих моделей .- К.: Тех-ника, 1984.- 350 с.
- Ивахненко А.Г., Степашко В.С. Помехоустойчивое моделирование. – К.: Наук. Думка, 1985.- 300 с.
- Ивахненко А.Г., Юрачковский Ю.П. Моделирование сложных систем по эксперимен-тальным данным .- М.: Радио и связь, 1987.- 120 с.
- Файнзильберг Л.С. Синтез информационных технологий обработки сигналов в зада-чах косвенного контроля и диагностики // УСиМ . – 1998. - № 2 .- С. 40-47.
- Белкин А.В., Левин М.Ш. Принятие решений: комбинаторные модели аппроксимации информации. - М.: Наука, 1990.- 160 с.
- Иванцов Г.П. Теплообмен между слитком и изложницей .- М.: Металлургиздат, 1951.- 39 с.
- Новая технология производства пралиновых конфет / Р.Г. Зобова, М.А. Талейсник, Л.П. Игнатьева, В.И. Демидов.- М.: Легкая и пищевая промышленность, 1983. – 72с.
- Технология // Советский энциклопедический словарь .- М.: Советская энциклопедия, 1988.- С. 1330.
- Трегуб В.Г. Автоматизация периодических процессов в пищевой промышленности, – К.: Техника, 1984. – 160 с.