Время распространения акустического сигнала в ультразвуковом расходомере
N. N. Antonov and I. A. Kolmakov
Перевод с английского: Головина А.К.
Источник: Электронный ресурс УРАН
Статья рассматривает,что в теории ультразвуковых расходомеров плоская волна излучается [1]; и прямое распространение (в направлении потока) и обратное распространение (против потока) симметричны, и поэтому есть полное балансирование дифракции. Действие это происходит за определенное время, которое равно разнице между временами распространения от источника к детектору и назад.
Фактически, волна в близкой зоне (зона Fresnel) не плоская, и это происходит постепенно к сферической форме как расстояние от исходных увеличений [2]. Однако, симметрия передних и обратных волн нарушена, поэтому используется диффракционный эффект. В статье приведена идеализация эффекта, волны могут приводить к значительной погрешности.
Мы пренебрегаем детальной формулировкой выравниваний и решений, а всего лишь отмечаем, что вибрации исходной пластины представлены, как обычно, с помощь.ю поршневой системы; мы также пренебрегаем эффектами любых карманов в стенах, отображениями от границ перемещения и неподвижные СМИ, эффекты от ветра, и Ликаси. Ниже приведенно выражения для среднего давления набора в пластине обнаружения и в течение времени сигнала распространения от радиатора к детектору:
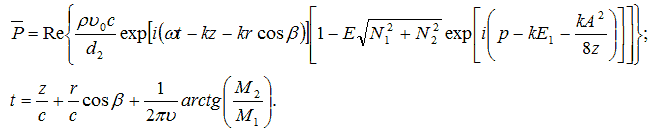
где Re - реальная часть выражения, появляющегося в пределах скобок, ρ - плотность вещества , ν0 - амплитуда вибрационной скорости, c - скорость звука вещества,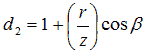 
z - расстояние между пластинами отправления и получения (они коаксиальны и параллельны), β - угол между акустическим каналом и трубчатой формы, 
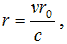v - скорость потока жидкости, 
d - диаметр трубы, ω - частота, k - количество волн, 
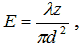и
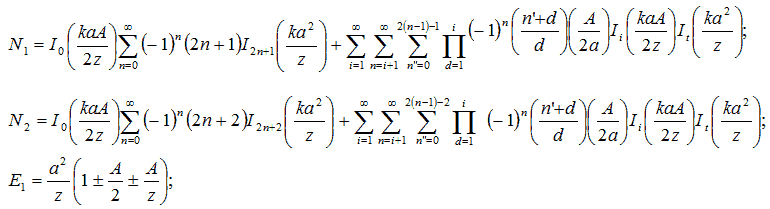
где α - радиус пластины (берем для простоты испускания и получения пластины , не возникает никакой трудности в описании различных пластин в радиусах),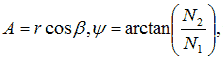 
ν - вибрационная частота испускающей пластины, и 
.
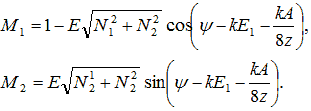Тройными суммами в выражениях для и , можно принебреч, если скорость потока низкая, поскольку взносы становятся незначительными. Расчеты проводились на ЭВМ М-222, и некоторые результаты показаны на рис. 1.
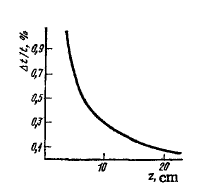
Рис.1 - Результаты проводимых экспериментов
Это свидетельствует о дифракционной коррекции, принятых за время дифференциальных распространения, как функции от расстояния между источником и приемником. По оси абсцисс отложен z, в то время как по оси ординат - отношение дифракции коррекции времени , представляющие собой разницу в распространении раз в прямом и обратном направлениях.Это безразмерная величина.
Это безразмерные представление удобно, потому что нет скорости зависимости Δt/t, хотя Δt на самом деле увеличивается с медленной скоростью. Расчеты проводились при следующих значениях параметров: a=1 см; β=15°; ν1 МГц; и z=r0 повсеместно рассматриваться как 2 см. Рисунок 1 показывает, что кривая резко падает при z увеличивается (например, разница коррекции только 0,002% для z = 40 см), который показывает, что расстояние между пластинами должно быть увеличено чтобы свести к минимуму этот источник погрешностей (это увеличивает длину карманов). Однако, это не всегда практично и не имеют недостатков (например, увеличивается погрешность в скорости потока измерений, возникающие из-за отсутствия параллелизма, отклонение от коаксиального положения и т.д.). Кроме того, есть определенные изменения в относительном амплитудном давлении для значения плоской волны , которая зависит от скорости потока.
Литература
- G.I. Birger and N. I. Brazhnikov, Ultrasonic Flowmeters [in Russian], Metallurgiya, Moscow (1964).
- M.B. Gitis and A. S. Khimunin, Akust. Zh., 14, No. 3 (1960).