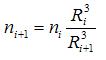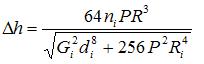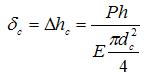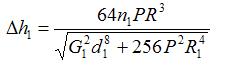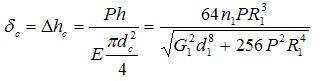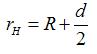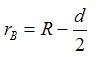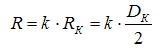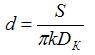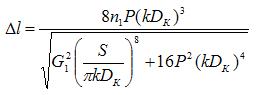Уточнение метода контроля натяжения канатов шахтной
подъемной установки

Авторы: Н.Г. Винниченко, О.В. Казаков

Источник: Сборник публикаций научных работ студентов и преподавателей
ДонНТУ, 2010 г.

Аннотация

Проанализированы известные в настоящее время методы контроля натяжения канатов и выбран наиболее оптимальный. Уточнена математическая модель каната как винтовой цилиндрической пружины. Определена зависимость удлинения каната от величины нагрузки и его конструктивных особенностей.

Ключевые слова: канат, контроль, перегрузка, натяжение, датчик, подъемная установка, математическая модель.

Актуальность задачи

Актуальность создания электронной системы, которая отслеживала бы равномерность натяжения канатов, обусловлена требованиями пункта 4.12.22 НПАОП 10.0-1.01-05 «Правил безопасности в угольных шахтах» о необходимости контроля относительной перегрузки канатов шахтной многоканатной подъемной установки [1].

Общая постановка проблемы

При эксплуатации многоканатных подъёмных установок часто происходит разбаланс канатов вследствие разной степени их удлинения. При этом нагрузка на канаты распределяется неравномерно, и те из канатов, удлинение которых больше, подвержены действию большей части нагрузки. Это приводит к неравномерному износу футеровки шкивов подъемных установок, перегрузке отдельных канатов, особенно при движении сосуда на этапе ускорения или торможения. Создаются предпосылки для аварийной ситуации, сопровождающейся обрывом и падением подъемных сосудов, разрушением стволов, а на людских подъемах – травмированием и гибелью людей.

Анализ известных решений

В СССР в начале 60-х годов для измерения натяжений в канатах был создан прибор (разработка МакНИИ), основанный на измерении частоты поперечных колебаний каната ограниченной длины, которая (частота) непосредственно связана с натяжением. Однако из-за сильно выраженного дисперсионного характера таких колебаний идентификация численных значений усилий приводила к неоднозначным результатам, из-за чего прибор не нашел практического применения [2].

Самым простым и доступным способом измерения натяжений является так называемый волновой, предложенный в конце 50-х годов шведскими инженерами (теперь этот способ иногда так и называют — шведским) [2].

Суть этого способа состоит в следующем. Пусть вертикально висящий массивный канат длиной L и погонной массой q=q_Г в нижней точке растянут силой Р. Считается, что нижняя точка в поперечном направлении не перемещается. В окрестности подвеса верхнего конца каким-либо способом возбуждается поперечная волна в канате (нечто подобное солитону – уединенной волне), которая, отразившись от неподвижной концевой массы, спустя некоторое время Δt, возвращается в исходную точку, в которой возбуждалась волна, и воспринимается специальным прибором. Оказывается, что величина Р непосредственно связана с величиной Δt, следовательно, по ее измеренному значению можно определить натяжение каната Р в нижнем сечении. В случае достаточно длинных канатов (L > 600 м) изложенный способ определения усилий дает удовлетворительные результаты при использовании обычного секундомера с возбуждением и приемом отраженного сигнала при помощи руки.

Недостатками такого способа измерения натяжения является необходимость использования человека в качестве приемника отраженного сигнала и невысокая точность измерений обычным секундомером.

Для контроля натяжения канатов проходческих лебедок используются ограничители натяжения канатов ОНК-1М.У1 (в 80-х годах XX ст. выпускался институтом ВНИИОМШС г. Харьков [3], в настоящее время – компанией «Сибтензоприбор» г. Новосибирск [4]).

Недостатком данного ограничителя является необходимость перегиба каната, а также использование рычажно-роликовой системы, постоянство точности работы которой при действии продолжительных динамических нагрузок при движении каната обеспечить достаточно сложно. Также к недостаткам можно отнести: ограниченные диапазоны диаметров контролируемых канатов и пределов контролируемых нагрузок; невысокую точность установления предела перенапряжения (погрешность составляет 10% от номинальной нагрузки ограничителя); относительно быстрый механический износ рычажно-роликовой системы.

В НИИГМ им. М.М. Федорова разработан комплекс технических средств, обеспечивающих безопасную эксплуатацию шахтных подъемных установок КТС БПУ. Комплекс предназначен для контроля натяжения канатов, защиты от провисания и напуска, контроля срабатывания парашютных устройств, контроля местоположения клети в стволе, защиты от жесткой посадки клети, передачи и представления информации машинисту подъема [5].

Датчик натяжения данного комплекса, размещаемый на канате над подвесным устройством подъемного сосуда, осуществлял контроль нагрузки на канат по величине удлинения каната. Во время эксплуатации датчик показал невысокую надёжность работы и практически осуществлял только контроль напуска каната (вертикальность положения каната).

Таким образом, на данный момент в Украине не создано автоматизированных систем, обеспечивающих надежный контроль натяжения канатов шахтных подъемных установок.

В связи с указанными недостатками существующих методов контроля натяжения, предлагается продолжить работы по совершенствованию технических средств, использующих метод контроля нагрузки на канат по величине удлинения последнего.

Данный метод обладает такими преимущества над перечисленными выше методами:

1. Высоким быстродействием, обусловленным в основном только временем передачи
   информации по радиоканалу.
2. Высокой точностью измерений (обусловлена непосредственным измерением
   фактического усилия на канат).
3. Высокой надёжностью работы в различных климатических условиях и во всем
   допустимом диапазоне нагрузки канатов (т.к. чувствительные элементы не
   подвержены действию больших механических нагрузок).
4. Простотой обеспечения взрывобезопасности применяемых технических средств.

Постановка задач исследования

Для реализации метода необходимы датчики линейных перемещений, для обоснования параметров и правильного выбора конструктивных типов которых требуется определить ожидаемые величины удлинений. Поэтому задачами данного исследования являются:

1. Уточнение математической модели каната как винтовой цилиндрической пружины.
2. Определение зависимости удлинения каната от величины нагрузки и его
   конструктивных особенностей.

Решение задач и результаты исследований

В расчётной схеме (рис. 1) представим каждый слой в виде винтовой пружины кругового поперечного сечения диаметром d. Предположим, что винтовая пружина кругового поперечного сечения подвергается действию сил Р, направленных по оси, и какой-либо виток лежит в плоскости, мало отличающейся от плоскости, перпендикулярной к оси пружины. Рассматривая равновесие верхней части пружины, ограниченной осевым сечением, например mn (рис. 1,2), можно заключить из уравнений статики, что усилия по поперечному сечению mn витка приводятся к срезающей силе Р, приложенной в центре тяжести поперечного сечения, и к паре сил, действующей в плоскости поперечного сечения в направлении против хода часовой стрелки [6].

Рисунок 1 – Винтовая цилиндрическая пружина

Радиус пружины считается неизменным в процессе её растяжения: R_i = R = const.

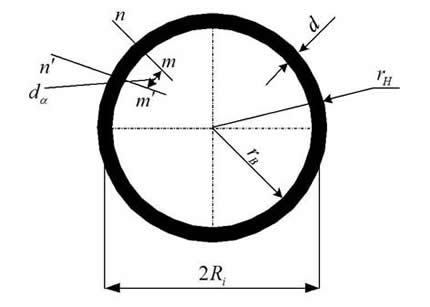
Рисунок 2 – Звено винтовой цилиндрической пружины

В работе [6] получено следующее выражение для опускания пружины:

(1)

где G – модуль упругости при сдвиге; E – модуль упругости при растяжении; m –коэффициент Пуассона; d – диаметр поперечного сечения витка; Δt – полное опускание пружины (см. рис. 1); i = 1,..., k – номер слоя;  n – число витков.

Приравнивая опускания каждого слоя (1), получим

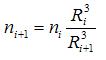(2)

Учитывая изменение радиуса пружины при её растяжении, принимается допущение о постоянстве длины витка пружины, т.е. 2πR = const.

Получено

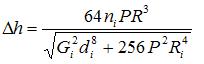(3)

Приравнивая опускания каждого слоя (3), получим

(4)

При наличии стального сердечника диаметром dc необходимо учесть его удлинение под действием силы Р. Считая сердечник однородным длинным цилиндром, по известным зависимостям сопротивления материалов получаем

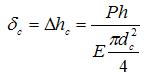(5)

Для первого слоя согласно зависимости (2) его опускание равно

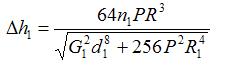(6)

Приравнивая опускания сердечника (5) и первого слоя (6), получим

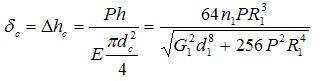(7)

Рассмотрим удлинение каната на конкретном примере. Возьмём канат двойной свивки типа ЛК-Р конструкции 6x19(1 + 6 + 6/6) + 1 о.с. (ГОСТ 2688 – 80). Поперечное сечение данного каната изображено на рис. 3.

Рисунок 3 – Поперечное сечение каната ГОСТ 2688 – 80

Для представления рассматриваемого каната в виде винтовой пружины (рис. 3) введём следующие соотношения:

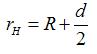(8)

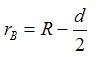(9)

где r_Н – наружный радиус звена винтовой цилиндрической пружины; r_В – внутренний радиус звена винтовой цилиндрической пружины; R – радиус пружины.

Тогда площадь круга, заключенная между радиусами, вычисляется по формуле:

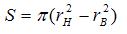(10)

Подставляя (8) и (9) в (10), получаем

(11)

Преобразуя (11), соотношение для диаметра поперечного сечения винтовой пружины выглядит так:

(12)

Введём коэффициент взаимосвязи радиуса каната и радиуса пружины k:

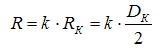(13)

Тогда с учётом соотношения (13) формула (12) принимает вид:

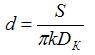(14)

Используя (14), получаем выражение для расчёта удлинения (Δl) рассматриваемого каната:

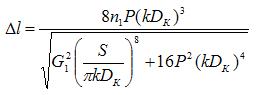(15)

На основании установленной зависимости при коэффициенте взаимосвязи радиуса каната и радиуса пружины k = 0,3 получены следующие величины удлинений канатов указанных диаметров (рис. 4).

Рисунок 4 – Удлинение каната ГОСТ 2688 – 80 в зависимости от величины нагрузки и конструктивных особенностей

Таким образом, по мере роста нагрузки на канат наблюдается увеличение величины удлинения каната. В качестве минимальной нагрузки рассматривался вес ненагруженного подъемного сосуда, поэтому величины удлинений в данном случае минимальны. По мере уменьшения диаметра каната, уменьшается площадь сечения проволок, что приводит к увеличению удлинения каната.

Выводы

1. Проанализированы существующие методы контроля натяжения канатов.
2. Как наиболее оптимальный для разрабатываемой электронной системы выбран
   метод контроля натяжения канатов по величине удлинения последних.
3. Уточнена математическая модель каната как винтовой цилиндрической пружины.
4. На примере каната ГОСТ 2688 – 80 установлены величины ожидаемых удлинений в
   зависимости от величины нагрузки и конструктивных особенностей каната.

Литература

1. Правила безопасности в угольных шахтах: НПАОП 10.0 – 1.01 – 05. – Луганск, 2005. – 162 c.
2. Бежок В. Р., Дворников В. И., Манец И. Г., Пристром В. А., общ. ред. Б. А. Грядущий, В. А. Корсун. Шахтный подъем: Научно-производственное издание – Донецк: ООО «Юго - Восток, Лтд», 2007. – 624 с, 494 ил., 233 библиогр.
3. Руководство по определению величин натяжения направляющих канатов при
   проходке стволов шахт. – Харьков: ВНИИОМШС, 1970. – 44 с.
4. Машины и оборудование для шахт и рудников: Справочник / С. Х. Клорикьян,
   В. В. Старичнев, М. А. Сребный и др. – 6-е изд., стереотип. – М.: Издательство
   Московского государственного горного университета, 2000. – 471 с.
   ISBN 5-7418-0173-0
5. Коваль А.Н., Мялковский В.И., Чехлатый Н.А. Комплекс технических средств
   безопасности подъемных установок // Уголь Украины. – 2008. – №7, c. 30-33.
6. Великанов Н.Л., Примак Л.В., Сапрыкин Ю.М. О прочности грузонесущих стальных
   канатов // Строительные и дорожные машины. – 2008. – №10, c. 40-43.