Разработана математическая модель электропривода шахтного аккумуляторного электровоза АМ8Д на основе вентильного индукторного двигателя (ВИД), предназначенная для анализа электромеханических процессов в пусковых и буксовых режимах работы рудничного электровоза, для обеспечения оптимальных тяговых характеристик электропривода и алгоритма управления вентильным индукторным двигателем.

За последнее время достижения в области силовых полупроводниковых приборов позволили приступить к созданию современных приводов для электроподвижного состава. Пусковые режимы работы тягового электропривода на номинальной и максимальных частотах вращения, а также режим электрического торможения для рудничного контактного электровоза были рассмотрены в [1]. Настоящая статья посвящена вопросам обеспечения оптимальных тяговых характеристик электропривода шахтного аккумуляторного электровоза в режиме пуска и буксования. При проведении расчетных исследований использовано программное обеспечение по математическому моделированию электромагнитных процессов в вентильном индукторном двигателе с учетом насыщения магнитной системы [2]. При выборе зубцовой зоны были использованы рекомендации, приведенные в [3, 4]. В процессе проведения расчетных исследований зубцовая зона двигателя, площади основных сечений ярма статора и ротора не изменялись.

Построена общая структурная схема электромеханической системы с учетом источника питания ограниченной мощности и определены требования к системе автомтического управления электроприводом.

В основу расчета переходных процессов положены уравнения электромагнитного и электромеханического равновесия в системе тягового электропривода [5].

Схема усилий и моментов, действующих на колеса электровоза при работе привода в режиме буксования, показана на рис. 1.

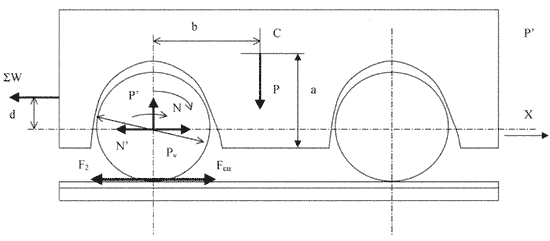
Рис.1. Схема усилий и моментов

В основу математической модели пускового режима тягового электровоза поло- жена следующая система уравнений:

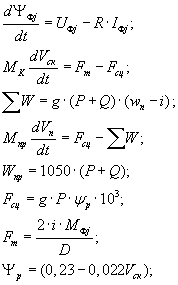
где V_ск – скорость скольжения колес при буксовании; V_П – скорость поезда; ∑W – суммарное сопротивление движению поезда; P – масса электровоза; Q – масса электропоезда; i – передаточное отношение; ψp – коэффициент сцепления колес с рельсами. Общее время разгона поезда составляет примерно 90 сек.

Коэффициент сцепления колес с рельсами в имитационной модели изменялся ступенчато от значения ψp1 = 0,23 до значения ψp2 = 0.1 посредством сумматора и ступенчатого входного воздействия. Время наступления пробуксовки задавалось равным 5 с. Числовые данные поезда с вагонетками и электровозом АМ8Д: Q = 312 т – полный вес поезда; P = 14 т – вес электровоза; w_i = 1,5•w_o = 1,5•4 = 6 Н/кН. Уклон пути принят равным i = 3 ‰

При движении поезда по рудничным откаточным путям коэффициент сцепления изменяется в широких пределах. При реализации тяговых усилий в процессе разгона поезда в некоторых случаях (увеличение сопротивлению движению, снижение коэф- фициента сцепления и т.д.) выполняется условие F_m>F_сц. Работа привода происходит в зоне избыточного буксования. В соответствии с M_прdV_n/dt = F_сц – ∑W это приведет к увеличению ускорения скольжения и, следовательно, к повышению потерь энергии на буксование.

В зависимости от сочетаний параметров привода электровоза и характеристики сцепления возможны установившийся или разносный режимы избыточного буксования. При разносном режиме буксования происходит автоматическое увеличение скорости буксующих колесных пар при уменьшении их нагрузки. Этот режим работы обусловливает значительную долю потерь энергии на буксование колес электровоза. Поэтому он является нежелательным.

На рис. 2. представлена имитационная модель аккумуляторного рудничного электровоза АМ8Д совместно с вентильно-индукторным двигателем. Математическая модель разработана при помощи программы MatLab 6.5 Release 13 [6]. Программа MatLab содержит широкий спектр типовых динамических звеньев, как линейных, так и нелинейных [7].

Рис. 2. Математическая модель аккумуляторного электровоза на основе ВИД

Рис. 3. Режим пуска при одинаковых пусковых условиях для двигателей: Vп – скорость поезда; Vск – скорость скольжения

Разработанная математическая модель электропривода электровоза обеспечивает оптимальные тяговые характеристики электропривода электровоза. Результаты расчета пускового и буксового режимов подтверждают, что использование ВИД в приводе электровоза позволяет эффективно использовать энергию аккумуляторной батареи при работе электровоза в зоне избыточного буксования.

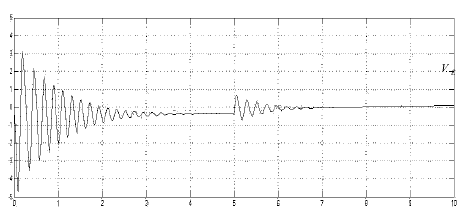
Рис. 4. Скорость колесных пар при одинаковом коэффициенте сцепления колес с рельсами

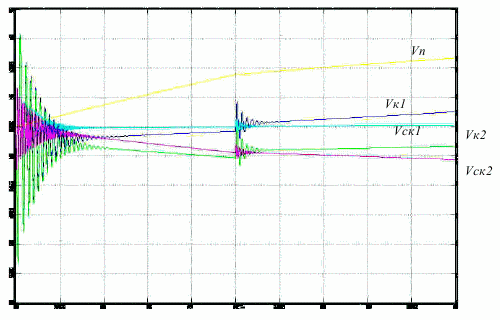
Рис. 5. Режим пуска при различных пусковых условиях для двигателей по пробуксовке колесных пар: Vп – скорость поезда; Vк1 – скорость колеса передней колесной пары; Vск1 – скорость скольжения первого двигателя; Vк2 – скорость колеса задней колесной пары; Vск2 – скорость скольжения второго двигателя

Литература

1. Коломейцев Л.Ф., Прокопец И.А., Пахомин С.А., Крайнов Д.В. Режимы работы тягового электропривода рудничного электровоза с трехфазным реактивным индукторным двигателем // Изв. вузов. Электромеханика. 2002. № 2. С. 18–22.

2. Коломейцев Л.Ф., Пахомин С.А., Прокопец И.А. и др. Расчет электромагнитных процессов в трехфазном управляемом индукторном двигателе // Сб. науч. тр. ОАО ВЭлНИИ. Электровозостроение. 1997. Т. 38. С. 234–245.

3. Пахомин С.А., Прокопец И.А. и др. Выбор соотношения зубцов статора и ротора в тяговом реактивном индукторном двигателе // Сб. науч. тр. ОАО ВЭлНИИ. Электровозостроение. 1997. Т. 38. С. 223–234.

4. Пахомин С.А. Влияние геометрии зубцового слоя и параметров питания на показатели вентильного реактивного индукторного двигателя // Изв. вузов, Электромеханика, 2000, № 1, С. 30–36.

5. Копылов И.П. Электромеханические преобразователи энергии. М.: Энергия, 1973.

6. Петрушин А.Д. Вентильно-индукторный привод: опыт разработки и внедрения //Приводная техника. 1998. №2.

7. Герман-Галкин С.Г. Компьютерное моделирование полупроводниковых систем в MATLAB 6.0: Учебное пособие. СПб: КОРОНА принт, 2001. 320с.

8. Волотковский С.А. Рудничная электровозная тяга. М.: Недра, 1981. С.390.