Методика принятия решений по выбору вида управляющего воздействия на основе экспертных оценок технологического процесса приготовления пралиновых масс

Автор: Тарасюк В.П, к.т.н, доцент кафедры ЭТ

Общая постановка проблемы. Кондитерское производство  является сегодня одним из важнейших составляющих пищевой промышленности, так как доля валового дохода кондитерских предприятий по оценкам некоторых экспертов составляет около 10 % всей прибыли региона. Анализ состояния автоматизации технологических процессов кондитерских производств показывает, что на действующих предприятиях из-за многомерности, больших объемов, нелинейности, многоканальности производственной информации отсутствуют эффективные интеллектуальные системы поддержки принятия решений операторов технологических процессов (ТП). Поэтому существует значительный потенциал повышения качества и выхода кондитерских изделий за счет автоматизации ТП, а именно на базе разработки гибридных экспертных систем   управления ТП [1]. В этом направлении формулировки и решения основной задачи повышения производительности ТП приготовления пралиновых масс на базе гибридных экспертных систем с использованием экспертных оценок является весьма актуальным и значительно развивает теорию автоматизированных систем управления технологическими процессами.

Анализ публикаций и разработок по теме. Для решения проблемы предлагается подход, основанный на оперативной идентификации параметров объекта управления (ОУ) с последующим синтезом оптимального управления в пространстве состояний [2]. Он включает три основные этапа – идентификация коэффициентов дискретной модели ОУ на основе экспертных оценок с использованием метода наименьших квадратов [3], вычисление текущих значений переменных пространства состояний и синтез оптимального управления.

Постановка задач исследований. Для реализации поставленных задач необходимо разработать алгоритм, который позволит обеспечить синхронность работы структурных элементов технологического процесса кондитерского производства на основании формализованных знаний и опыта экспертов. Проанализировать характеристики основного  показателя качества готовой продукции, сформировать целевую функцию управления технологическим процессом. Разработать алгоритм нахождения математических моделей, характеризующих состояние ТП путем обработки результатов эксперимента с учетом технологических ограничений и оценки адекватности полученных моделей.

Основной материал и результаты работы. Базовым технологическим процессом был выбран   технологический процесс  приготовления   пралиновой   смеси,   как   основной   части производства пралиновых конфет. Пралине представляет собой тонко измельченную кондитерскую массу, в состав которой входят: жир, орехи, сахарная пудра и добавки.

Анализ технологии и техники производства на кондитерских предприятиях показал, что приготовление пралиновых конфет осуществляется по технологической схеме, укрупненно представленной на рис.1. Сравнительный анализ технологических параметров пралиновой массы (ПМ) на различных стадиях показал, что одним из путей решения проблемы получения ПМ заданного качества является обеспечение качества распределения компонентов при получении предварительной рецептурной смеси, ее конечной температуры и количества в ней смеси жиров.

 

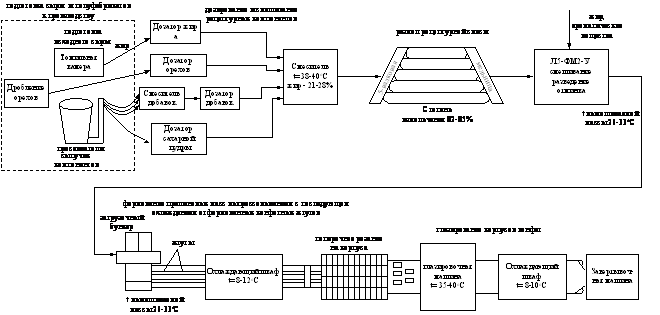
Рис. 1 Укрупненная схема технологической линии приготовления пралиновых конфет

 

В связи с этим было определено, что усовершенствование структуры автоматизированной системы управления технологическим процессом приготовления пралиновых масс возможно за счет включения в контур управления экспертных оценок, а именно за счет объединения всех функций обработки информации и управления в единой системе, с учетом автоматизации экспертных оценок [4].

Организация управления в АСУ ТП связана с необходимостью получения информации о ходе ТП и определения оптимального режима функционирования объекта, с реализацией найденных оптимальных управляющих воздействий [5]. Структура основных этапов в реализации управления ТП показана на  рис. 2.

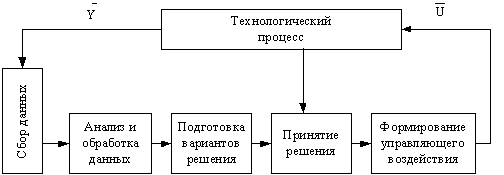
Рис. 2  Основные этапы в реализации управления объектом управления

 

Управления ТП приготовления пралиновых масс характеризуется большой размерностью вектора информации  (Y) (текущее состояние ТП), разными методами ее обработки и формами использования полученных результатов. Обеспечение оптимального хода процесса в АСУ ТП возможно за счет реализации в системе множества взаимосвязанных операций: сбор, хранение, анализ и переработка информации о ТП; снятие показаний, регистрация или индикация одних переменных и регулирование других, реализация набора определенных решений по управлению (U).

Для обеспечения оперативности управления ТП приготовления пралиновых масс и адекватности математической модели управления качеством система управления должна базироваться на принципах получения статических и динамических характеристик непосредственно на объекте в процессе управления [6]. При создании математической модели  объекта различают два основных этапа: определение структуры модели, т.е. набора функциональных и позиционных ограничений,  качественный вид последних; расчет числовых значений коэффициентов ограничений. Наиболее часто используется подход к построению модели объекта, заключающийся в задании структуры в виде зависимости вектора выходных координат комплекса Y от вектора его входных координат Х.

Рассмотрим основные положения по формированию структуры статической модели с постоянными относительными выходами для систем смешивания. Имеется система, в которой материальный поток  Х, состоящий из компонентов х₁, х₂,…х_n, перерабатывается (смешивается) в поток Y = (y₁, y₂, … y_n). Компоненты продуктов – это смеси из сырьевых компонентов, входящих в рецептуру. Выход продукта Y есть

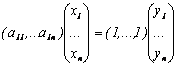.                                                 (1)

Основной задачей получения статических моделей, является отыскание связей между входными величинами X и выходными Y, т.е. определения коэффициентов связей (матрицы , i=1,…m ). Возникает задача определения структуры и параметров  самоорганизующейся модели рассматриваемого процесса [7]. В общем виде она имеет вид

  ,                                           (2)

при ,

где – неизвестные функции, формируемые в классе опорных функций ;

       – задаваемая длина полинома модели;

       – степень полинома;

 – неизвестные коэффициенты модели, подлежащие определению;

        Ф – критерий адекватности при отборе модели [7].

В этом случае модель в процессе управления формируется непосредственно на объекте путем задания класса опорных функций, степени и длины полинома. В качестве критерия адекватности используется среднеквадратичное отклонение  выходной координаты модели  от координаты частной модели в выборке исходных данных N:

.                                           (3)

Этот критерий удобно использовать при самоорганизации моделей в таком режиме, когда модель корректируется при небольшом изменении исходных данных в выборке.  Тогда алгоритм самоорганизации должен содержать некоторый источник моделей, в котором хранятся варианты моделей.

Таким образом, при построении системы управления технологическим процессом целесообразно задавать не модель в окончательном виде, а метод получения адекватной модели из опорных функций непосредственно на объекте на обучающей выборке, при этом структура модели зависит от выбора  опорных функций, числа аргументов и длины аппроксимирующего полинома. В основе решения этой задачи лежит многопараметрический вычислительный метод анализа многокомпонентных смесей, разработанный Р.Б.Поповым [7]. В ходе решения задачи применялись экспериментально установленные «состав-свойство» данные, полученные при использовании математических методов планирования и анализа эксперимента [8].

Был проведен анализ характеристик качества пралиновой массы. Определено, что пралиновые массы, представляют собой вязкопластичные структурированные дисперсные системы с характерной аномалией вязкости. Анализируя рассматриваемый технологический процесс, видно, что качество готового продукта  характеризуется  следующими параметрами (рис.3)

Z = f(h, j₁, g, Т, l),                                                                       (4)

где h– вязкость готовой смеси, Па^.с; j₁ – влажность пралиновой смеси, %; g – дисперность  пралиновой смеси; Т – температура смеси, °С; l – жирность смеси, %.

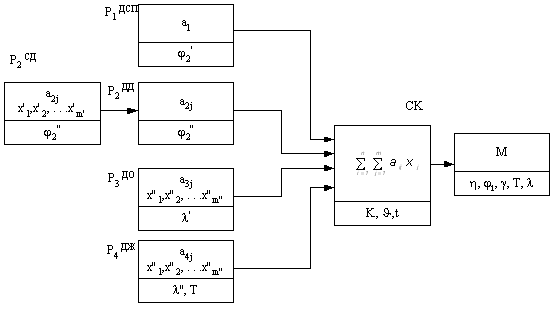
Рис. 3 Схема приготовления пралиновой смеси автоматизированной рецептурной станцией

На рис. 8 обозначено: СК — смеситель компонентов; ДСП – дозатор сахарной пудры; ДД – дозатор добавок; СД – смеситель добавок; ДО – дозатор орехов; ДЖ – дозатор жира; М - порция готовой пралиновой массы (ПМ). Реологические характеристики ПМ зависят от содержания жира, температуры массы, влажности, влияния механических воздействий, т.е. для получения продукции заданного качества необходимо учитывать: l– процентное содержание жира; J - скорость перемешивания, с^-1; t – длительность одного цикла приготовления пралиновой смеси, Т - температуру смеси; К -оптимальный состав однородной ПМ.

 

Если принять, что значения масс компонентов, определенные в режиме реального времени будут соответствовать заданной точности, то качество получения высокооднородной смеси К будет определяться точностью дозирования массы доз каждого компонента. Задачу получения однородной смеси можно представить в виде целевой функции

К = g(P₁,P₂,...,P_n),                                                                         (5)

P₁,P₂,...,P_n — массовые доли компонентов, входящих в рецептуру пралиновой смеси, по отношению к соответствующему дозатору. Степень достижения этой цели зависит от переменных P_і , которые позволяют максимизировать функцию К, как обобщенного показателя качества при соблюдении всех требований технологического процесса, т.е. К(P₁,P₂,...,P_n)® max.

Для оценки зависимости вязкости пралиновой массы от вышеперечисленных факторов были разработаны план однофакторного и многофакторного экспериментов. На основании проведенного регрессионного анализа были получены модели влияния l, J, Т на h готовой смеси. Объектом исследования являлось изделие «Белочка», выходной величиной У – вязкость смеси, а входными факторами: х₁ – температура; х₂ – процентное содержание жира; х₃ - скорость перемешивания. Задача ставилась следующим образом: определить опорную функцию, степени  и длину полинома, т.е. выбрать вид функций отклика в случае однофакторной модели Y₁=f(х₁), Y₂=f(х₂), Y₃=f(х₃), и многофакторной Y₄=f(х₁,х₂,х₃). После обработки результатов эксперимента были получены следующие результаты: коэффициенты корреляции значительные: для функции Y₁, r₁ =0,904; для функции Y₂ , r₂ =0,846; для функции Y₃ , r₃ =0,951, что подтверждает гипотезу о решающем влиянии вышеперечисленных показателей на качество конечного продукта. Затем при помощи выборочного корреляционного отношения было доказано что входные и выходные величины связаны нелинейной корреляционной связью и полученные в результате исследования регрессионные модели имеют вид:  

, , ,

,

где , ,, - коэффициенты, значения которых зависят от вида пралиновой массы. В частном случае, для изделия «Белочка» модели однофакторного эксперимента приняли вид:  ,

,,

После моделирования расчетных и экспериментальных моделей, были получены зависимости представленные на рис. 4 – это зависимости вязкости различных масс от вышеперечисленных параметров.

Кроме того была проанализирована многофакторная регрессионная модель:

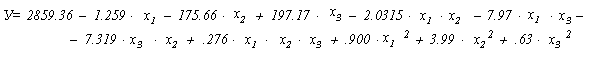
а)

б)

в)

Рис. 4 Зависимость вязкости пралиновых масс от температуры (а), процентного содержания жира (б), скорости перемешивания (в), , , , - экспериментальные значения

 

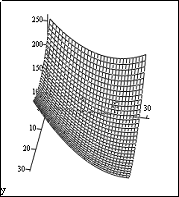
Были построены поверхности отклика и их проекции на плоскость, с учетом фиксации каждого параметров на трех уровнях: минимальный, средний и максимальный  с учетом вариации двух параметров на всем интервале исследования (рис.5).

Х3 = 2.3 с-1	Х3=6.15 с-1	Х3=10 с-1

Рис. 5 Некоторые примеры поверхности отклика регрессионных моделей основного

показателя качества

При проверке значимости коэффициентов регрессионных моделей (по критерию Фишера) все они оказались значимы, а модели адекватными при доверительной вероятности 0,95.

Проведенный анализ дл необходимый материал для построения алгоритма принятия решений по выбору вида управляющего воздействия при управлении технологическим процессом приготовления пралиновых масс на основе экспертных оценок. Полученные модели были положены в основу автоматизированного модуля системы управления ТП на основе экспертных оценок текущей ситуации и оценки качества партии готовой смеси.

Представление знаний – один из ключевых моментов обеспечения процесса принятия управленческого решения, т.е. преобразование исходной информации в управляющие воздействия.  В целом все факторы, от которых зависит эффективность выбора решения, можно разбить на две группы:

- контролируемые  факторы, выбор которых определяется  экспертным анализатором при управлении рецептурной станцией:

Х={Х₁,...Х₅, Х₆, Х₇, Х₈},                                                        (6)

где Х_{1, ...}  Х₅  – скорость дозирования компонентов в дозаторах;  Х₆ – степень качества  пралиновой массы (вязкость), Х₇ – температура готовой смеси, Х₈ – процентное содержание жира;

- неконтролируемые факторы, характеризующие условия, в которых осуществляется выбор и на которые экспертный анализатор влиять не может.

Последние в зависимости от информированности о них подразделяют на три группы:

- детерминированные неконтролируемые факторы — случайные фиксированные величины, значения которых полностью известны: А₁ – залипание компонентов в дозаторах;  А₂ – отказ измерительной аппаратуры;    А₃ – отказ сигнальной аппаратуры.

- стохастические неконтролируемые факторы — случайные процессы с известными законами распределения, т.е. измеряемые возмущающие воздействия:  Y₁– влияние влажности помещения;      Y₂ – несоответствие исходного сырья ГОСТ.

 - неопределенные неконтролируемые факторы, для каждого из которых неизвестны значения в момент принятия решения:   Z₁ –  механическая поломка исполнительных механизмов;   Z₂ – заклинивание механизмов дозаторов.

В соответствии с выделенными факторами критерий оптимальности принятия решений можно представить в виде

                                   F = F(X₁, X₂,..., X₈, А₁, ..., А₃, Y₁, Y₂, Z₁, Z₂, t).                                 (7)

Величины X, A, Y, Z в общем случае могут быть скалярами, векторами, матрицами. Значения контролируемых (управляемых) факторов обычно ограничены рядом естественных причин, например ограниченностью располагаемых ресурсов. Математически эти ограничения записываются в виде

g_i = g_i(X₁, X₂,..., X₈, А₁, ..., А₃, Y₁…Y₃, Z₁, Z₂, t) {£ ,=, ³} b_i, i=1,m           (8)

Условия (4.27) определяют области определения пространства ОХ, ОА, ОУ, ОZ, внутри которых расположены возможные (допустимые) значения факторов Х₁, X₂, ..., X₈, А₁, ...А₃, Y₁…Y₃, Z₁, Z_2.

Аналогично могут быть ограничены и области возможных значений неконтролируемых факторов, поскольку критерий оптимальности есть качественная мера степени достижения цели управления. математически цель управления выражается в стремлении к максимально возможному уменьшению значения критерия f, что можно записать в виде f® min.  средством достижения этой цели является соответствующий выбор r1, r2, ..., r6  управлений из областей определения их допустимых значений.

Таким образом, общая постановка задачи принятия решений  может быть сформулирована следующим образом: при заданных значениях X_1орт, X_2opt,..., X_8opт и характеристиках фиксированных неконтролируемых А₁, ..., А₃, Y₁…Y₂ с учетом неопределенных факторов Z₁, Z₂ найти оптимальные значения R_i из областей их допустимых значений, которые по возможности обращали бы в минимум критерий оптимальности F. На основании рассмотренных факторов можно составить алгоритм оценки нарушений и принятия решений по выбору вида управляющего воздействия. Структура алгоритма оценки нарушений приведена на рис.6.

Рис. 6 Структура алгоритма оценки нарушений и принятия решений по выбору управляющего воздействия

 

            Выводы. Впервые предложена концепция гибридных экспертных систем управления локальным ТП приготовление пралиновых масс на основе разработанной математической модели процесса приготовления пралиновой массы с использованием релевантных параметров (температура, процентное содержание жира, скорость перемешивания), а также на основе экспертного анализа критических производственных ситуаций с использованием продукционной модели представления знаний и механизма вывода непроцедурного типа, что обеспечивает повышение оперативности и качества кондитерського производства пралиновых масс.

Задача автоматизированного управления локальным ТП приготовление пралиновых масс решено на базе теории самоорганизации О.Г.Ивахненко для структурно- параметрической идентификации моделей объектов управления, а также на основе анализа производственных ситуаций и критических моментов при дозировании в рецептурных станциях с использованием продукционной модели представления знаний и механизма вывода непроцедурного типа, что обеспечивает повышение оперативности и качества производства пралиновых масс.

Дальнейшим развитием рассмотренных алгоритмов предполагается разработка автоматизированной системы с полной идентификацией объекта управления с использованием аддитивной процедуры усложнения модели.