Главная страница ДонНТУ Портал магистров ДонНТУ

Автобиография Реферат Индивидуальный раздел Отчет о поиске Ссылки

Исследование эффективности возбуждения акустических колебаний однопроводным излучателем под действием силы Лоренца. Разработка ЭМА-преобразователя. Приборная реализация

Н.Г. Лещенко, В.Ф. Мужицкий, В.Б. Ремезов

НИИИН МНПО "Спектр", Москва

Источник:http://www.mashin.ru/jurnal/autorart.php?id=9&autid=00101

     Рассматривается зависимость величины смещения при возбуждении акустических колебаний под действием силы Лоренца от глубины и величины рабочего зазора. Исследования проведены для однопроводного излучателя. В отличие от предшествующих исследований представлена плоскость, перпендикулярная оси излучателя. Проведено сравнение теоретических и расчетных данных. Описана конструкция ЭМА-преобразователя. Прибор, использующий преобразователь подобного типа, прошел апробацию на ряде предприятий.

     В работе [1] представлено исследование эффективности возбуждения акустических колебаний для различных типов излучателей в зависимости от электрофизических свойств материала, величины тока в преобразователе, зазора между преобразователем и материалом, глубины. Приведены графические зависимости, характеризующие эффективность возбуждения в зависимости от продольной координаты в плоскости, перпендикулярной оси излучателя. Так, к примеру, в [1] даны графические зависимости величины смещений для продольных и поперечных акустических волн, возбуждаемых однопроводным излучателем от продольной координаты. На рис. 12.9 работы [1] зависимости приведены для поперечных (сдвиговых) колебаний, на рис. 12.8 – для продольных. Сдвиговые колебания обозначены t, продольные – l. Графики построены для определенной координаты по оси Z, т.е. определенной глубины.
     Целью данной работы является разработка соответствующего математического аппарата и построение 3D-графических зависимостей для плоскости, перпендикулярной оси излучателя. Фактически такие графики являются диаграммами направленности. Смещения рассчитывались под воздействием только силы Лоренца, т.е. материал считается электропроводящим и немагнитострикционным. Такие материалы представляют наибольший интерес для неразрушающего контроля. Толщиномер ЭМАТ-100, преобразователь которого подобен по конструкции однопроводному излучателю и использовался для экспериментов, предназначен в основном для контроля электропроводящих и немагнитострикционных материалов.
     Ряд 3D-графических зависимостей для однопроводного излучателя приведен на рис. 1. Для исследований выбран ферромагнитный материал с высокой электропроводностью.

     Электрофизические параметры материала
1. Относительная магнитная проницаемость:
     - в направлении оси Y μy . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .11
     - в направлении оси Z μz . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .101
2. Удельная электропроводность материала σ, См/м . . . . . . . . . . . . . . . . .10*10^6
3. Удельный вес материала ρ, Н/м3. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 78*10^3
4. Скорость распространения колебаний, м/с:
     - продольных cl . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5920
     - сдвиговых сt . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3230
5. Магнитное поле (направление перпендикулярноповерхности)
     - индукция Вoz, Тл. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .1
6. Плотность тока в плоском однопроводном излучателе I, А/м. . . . . . . . 10
7. Частота тока в излучателе f, МГц . . . . . . . . . . . . . . . . . . . . . . . . . . . . .1
8. Расстояние от преобразователя до поверхности (рис. 1), мм . . . . . . . . 0,1
9. Излучатель . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Плоский однопроводной
10. Половина ширины излучателя d, мм [1] . . . . . . . . . . . . . . . . . . . . . . . 5

     Все графические зависимости построены для полупространства. Графики а–в на рис. 1 построены для различных диапазонов по глубине.
     В данном случае рассмотрено возбуждение сдвиговых колебаний, их проекция на ось Y. В нормальном магнитном поле такой вид колебаний является основным. В соответствии с обозначениями в [1] такие колебания обозначаются Uty.
     На рис. 1, а представлен график для диапазона глубин от 0 до 200 мм, на рис. 1, б – от 0 до 100 мм и на рис. 1, в – от 0 до 50 мм. Обозначения в формулах, приведенных в данной статье, аналогичны принятым в [1].

где а=1,i - в зависимости от четности; - трансформанта амплитудного значения спектральной плотности проекции смещения [1]; y, z - координаты по оси ординат и глубине; Cy - скорость распространения УЗК вдоль оси Y, ω - циклическая частота УЗК.
     Смещения на графиках даны в ангстремах (1 ангстрем = 0,1 нм). Графики, представленные на рис. 1, г и д выполнены для одного диапазона по глубине 20 мм. График на рис. 1. г позволяет наблюдать диаграмму по ширине (по оси ординат) от .15 до +15 мм, на рис. 1, д – от .5 до +5 мм.

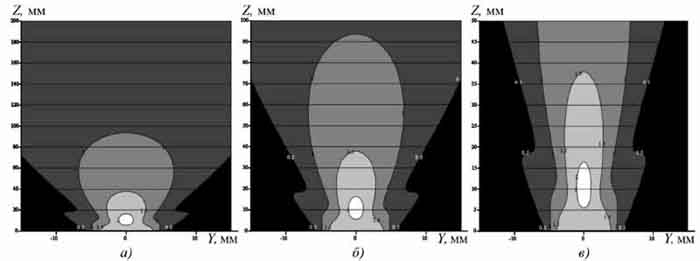
Рисунок 1 - 3D-графическая зависимость величины смещения при возбуждении акустических колебаний. Координата по глубине полупространства: а – от 0 до 200 мм; б – от 0 до 100 мм; в – от 0 до 50 мм; г – от 0 до 20 мм; координата по ширине (по оси ординат) ±15 мм; д – от 0 до 20 мм; координата по ширине (по оси ординат) ±5 мм

     Графики на рис. 1 демонстрируют возможности компьютерной обработки. На них наглядно представлены диаграммы направленности излучателя для разных диапазонов по глубине и для различной ширины зоны возбуждения. Таким образом, при необходимости любой интересующий исследователя участок можно выделить для детального рассмотрения.
     Анализируя зависимости, представленные на рисунках 1–5, можно сделать следующие выводы.
1. Независимо от глубины максимум смещения всегда располагается по центру излучателя, т.е. диаграмма направленности перпендикулярна поверхности металла.
2. Максимум смещения располагается не на поверхности излучателя, а на определенной глубине, для выбранных конкретных данных – порядка 11 мм.
3. По мере удаления от максимума в сторону увеличения координаты в глубь полупространства интенсивность возбуждения падает.
     Разумеется, анализируя зависимость смещения от продольной координаты для одной определенной глубины, можно получить очень подробную графическую зависимость, практически с любой дискретностью. Так, на рис. 2 приведена графическая зависимость для сдвиговых колебаний, проекция на ось У – Uty при глубине 15 мм, дискретность отсчета 0,1 мм. Также зависимости могут быть использованы для детального анализа. 3D-зависимости, демонстрирующие эффективностьвозбуждения сразу во всей плоскости, перпендикулярной оси излучателя, позволят сразу, хотя и с некоторым приближением оценить величину смещения в любой точке плоскости.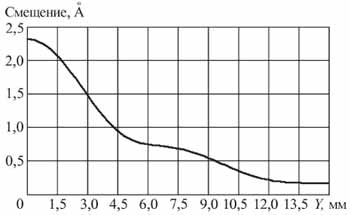

Рисунок 2 - Зависимость величины смещения от координаты по оси ординат

     Аналогичные зависимости, иллюстрирующие зависимость от зазора, представлены на рис. 3. Частота, электрофизические свойства материала, плотность тока, геометрические размеры преобразователя и прочие параметры такие же, как и для рассмотренных ранее случаев, но величина зазора – расстояние между преобразователем и границей полупространства различаются. Так, на графике рис. 3, а величина рабочего зазора выбрана 0,2 мм, б – 0,5 мм, в – 1 мм. Анализируя представленные зависимости, можно сделать вывод, что, кроме того, что при увеличении зазора уменьшается величина смещения, изменяется сам вид графика – зона эффективного возбуждения сужается, т.е., другими словами, диаграмма становится более направленной. Это согласуется с другими расчетными и экспериментальными данными, например [3, 4].

Рисунок 3 - Зависимость величины смещения от зазора. Величина зазора: а – 0,2 мм; б – 0,5 мм; в – 1 мм

     Следует заметить, что в действительности при экспериментальном исследовании зависимости от зазора графики будут иметь несколько иной вид. Дело в том, что величина постоянного магнитного поля Hoz в рассматриваемом случае считается постоянной, в действительности же она будет уменьшаться при увеличении зазора, что подробно изучено и описано, например в [5, 6]. Правильность теоретических расчетов была проверена экспериментально. Так, на рис. 4 приведен график, демонстрирующий, как величина принимаемого сигнала изменяется в зависимости от толщины материала.

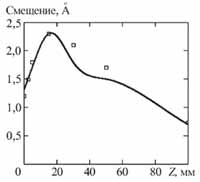
Рисунок 4 - Зависимость эффективности возбуждения акустических колебаний от глубины

     Эксперименты проводились с помощью преобразователя [2]. Электромагнитно-акустический преобразователь [2] представляет собой две плоские катушки(излучающую и приемную), расположенные на полюсе постоянного магнита. Катушка имеет форму, близкую к прямоугольной рамке [5]. Над полюсом магнита располагается только одна половина каждой из катушек [2], поэтому конструкция системы излучения получается близкой к однопроводному излучателю.
     Сравнительные графики, приведенные на рис. 4, демонстрируют совпадение расчетной кривой и экспериментальных данных. Некоторая неточность объясняется ошибками эксперимента. Преобразователь, построенныйпо принципу [2], использован в приборе ЭМАТ-100 [7]. Прибор позволяет контролировать толщину изделий различных электропроводящих материалов, как ферромагнитных, так и неферромагнитных. Диапазон контролируемых толщин 3…100 мм. Благодаря портативной конструкции прибор легко умещается в руке оператора. Питание прибора автономное, от двух аккумуляторов в корпусе РРЗ.
     Конструктивно прибор включает в себя электронный блок и два преобразователя – статический и динамический. Статический преобразователь позволяет работать на сильнокорродированных поверхностях, измерения можно вести через диэлектрический зазор, что, в частности, позволяет измерять толщину стенки газо- и нефтепроводов при наличии защитного покрытия толщиной до 1 мм [8]. Работа через диэлектрический зазор создает дополнительные возможности при измерении толщины изделий с горячей поверхностью до нескольких сотен градусов. В этом случае измерение ведут через теплоизоляционную прокладку, например через слой слюды или асбеста [9]. Таким образом можно выполнять кратковременные замеры – в течение нескольких секунд. Если же измерительный процесс должен идти на объектах с высокой температурой непрерывно, например в режиме мониторинга, преобразователь следует охлаждать, например, воздухом или водой.
     Таким образом, на базе разработанного математического аппарата был построен ряд графических 3D-зависимостей, которые по существу являются диаграммами направленности для однопроводного излучателя. Амплитуды смещений в ангстремах представлены на плоскости, перпендикулярной оси излучателя. Такое представление является исключительно удобным для экспресс- анализа. Было проведено сравнение полученных расчетных результатов с экспериментальными данными. В качестве источника возбуждения акустических колебаний был выбран ЭМА-преобразователь, описанный в [2]. Расчетные и экспериментальные данные практически совпали. ЭМА преобразователь [2] использован для возбуждения и приема акустических колебаний в приборе ЭМАТ-100 [7]. ЭМАТ-100 является бесконтактным толщиномером, обеспечивает возможность измерения на сильнокорродированных поверхностях, при высоких температурах. Кроме того, прибор комплектуется динамическим преобразователем, который снабжен специальными роликами, что позволяет вести непрерывный контроль при перемещении преобразователя. Прибор прошел апробацию на предприятиях ОАО "Газпром" и ОАО "РЖД".

Література

     1. Комаров В.А., Мужицкий В.Ф. Оценка физико-механических свойств твердых тел квазистационарным электромагнитным полем. – Ижевск: R&C Dynamics, 2004. – 345 c.

     2. Лещенко Н.Г., Мужицкий В.Ф., Ремезов В.Б. Патент на полезную модель № 31305 "Электромагнитоакустический преобразователь".

     3. Шкарлет Ю.М., Локшина Н.Н. Исследование электромагнитно-акустического преобразователя сдвиговых колебаний // Дефектоскопия. 1970. № 3. С. 3–12.

     4. Чабанов В.Е., Горделий В.И., Неволин О.В. Исследование теории и особенностей работы вихретоковых электромагнитно-акустических преобразователей // XVI Рос. науч.-техн. конф. "Неразрушающий контроль, диагностика", Санкт-Петербург, 9–12 сентября, 2002 г. СПб., 2002.

     5. Шкарлет Ю.М. Бесконтактные методы ультразвукового контроля. – М: Машиностроение, 1974. – 421 c.

     6. Сучков Г.М. Возможности современных ЭМА-толщиномеров // Дефектоскопия. 2004. № 12.

     7. Безлюдько Г.Я., Мужицкий В.Ф., Ремезов В.Б. Портативные электромагнитно-акустические толщиномеры (ЭМАТ) // Металл–оборудование–инструмент. Сентябрь–октябрь 2004.

     8. Мужицкий В.Ф., Ремезов В.Б., Детков А.Ю. Использование приборов технической диагностики для комплексного обследования трубопроводов и оборудования КС // XXIII тематический семинар "Диагностика оборудования и трубопроводов КС".

© ДонНТУ, Соломичев Роман Игоревич, 2010