Главная страница ДонНТУ Портал магистров ДонНТУ

Автобиография Реферат Индивидуальный раздел Отчет о поиске Ссылки

Имитационное моделирование измерительного канала температуры на основе экспериментальных данных

Тарасюк В.П., Зори А.А., Вовна А.В., Соломичев Р.И.

Донецкий национальный технический университет

Источник: Материалы 3 международной научно-технической конференции. — Донецьк, ДонНТУ — 2009, 358 с.

     Рассмотрена реализация способа имитационного моделирования измерительного канала температуры  на основе экспериментальных данных. Предложена математическая модель измерителя и представлены результаты экспериментальных исследований.

     Общая постановка проблемы. В данный момент в промышленности актуальным вопросом является отслеживание технического состояния оборудования, например, перегрев рабочих органов. Своевременное обнаружение аномального состояния препятствует созданию аварийной ситуации и остановке производства, благодаря быстродействию системы мониторинга. В ряде случаев очень существенно влияние температуры на рабочие органы, что приводит к изменению их физических параметров, например, температурного коэффициента линейного расширения металла, из которого данное оборудование изготовлено и может привести к аварийным ситуациям.
     Данную задачу позволяют решать методы неразрушающего контроля, в основе которых лежит принцип обработки измерительных сигналов. Как правило, измерительный канал представляет собой высокоточный (прецизионный) измерительный усилитель с датчиками, которые могут быть включены непосредственно на вход усилителя или посредством мостовых схем. Расчеты и обеспечение требуемых основных характеристик и параметров измерителя целесообразно проводить с использованием его имитационного моделирования [1].
     Общие положения моделирования измерителя. Структурной единицей рассматриваемой системы является канал измерения температуры на основе измерительного усилителя и терморезистора (датчика). Структурная схема измерителя температуры приведена на рис. 1. [2].

Рисунок 1 - Структурная схема измерительного усилителя

     Данная схема состоит из трех функциональных блоков: измерительный мост (ИМ), в одно из плеч которого включен терморезистор (ТР); дифференциальный усилитель (ДУ), который усиливает сигнал измерительного моста в требуемое значение напряжения на выходе, которое пропорционально значению измеренной температуры; нормирующий преобразователь (НП), который усиливает сигнал дифференциального усилителя в требуемое нормированное напряжения на выходе для дальнейшей его обработки в микропроцессорных информационно-измерительных системах или компьютерах.
     Для моделирования терморезистора и измерительного моста в EWB 5.12 PRO необходимо реализовать нелинейный входной сигнал, обусловленный нелинейностью терморезистора. Для этого можно воспользоваться встроенным элементом – полиномиальным источником напряжения (рис. 2), для преобразования сигнала температуры (в качестве сигнала температуры выступает сигнал напряжения с известной амплитудой), в напряжение, пропорциональное изменению сопротивления терморезистора.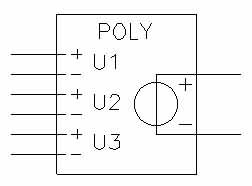

Рисунок 2 - Полиномиальный источник напряжения

     Полиномиальный источник — это источник напряжения, которым управляет определенная многочленная функция преобразовательного типа. Напряжением выхода, как функция напряжений на входах V1, V2 и V3, описывается следующим выражением:

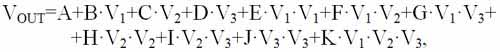
где A, B, C, D, E, F, G, H, I, J, K соответствующие коэффициенты полинома. В модели используются коэффициенты А. В, Е, К, так для получения минимальной погрешности аппроксимации градуировочной характеристики терморезистора достаточно третьей степени аппроксимирующего полинома [3].
     При этом возникает необходимость определения значений этих коэффициентов. При экспериментальных исследованиях были проведены многократные замеры сопротивления терморезистора при изменении температуры от 0 до 50 °С, в результате чего построена экспериментальная зависимость (рис.3), которая аппроксимируется по-линомом с помощью метода наименьших квадратов.
     Наибольшей чувствительностью обладает симметричный мост. Для средней точки диапазона измеряемой температуры (Т=25 °С), при которой значение сопротивления составляет 155 Ом, остальные три резистора моста применяются с тем же номинальным значением
     Рассчитывается пропорциональное изменение напряжения при изменении температуры Em(T):

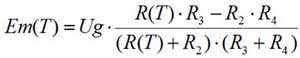
     Данную зависимость аппроксимируют полиномом с помощью МНК:

     В результате определен вектор значений В, который содержит коэффициенты полиномиальной функции Vout = A + B•V1 + E•V1•V1 + K•V1•V2•V3, для установки параметров полиномиального источника напряжения в EWB 5.12 PRO. Для моделирования выходного напряжения измерительного моста воспользуемся двумя полиномиальными источниками напряжения [2], в связи с использованием дифференциального усилителя на выходе измерительного моста.
     Получение математической модели ДУ сводится к расчету схемы, состоящей из трех операционных усилителей, два из которых (DA1 и DA2) обеспечивают высокое входное сопротивление и требуемое подавление синфазного сигнала, а третий (DA3) вычитание выходных сигналов DA1 и DA2. На выходах ДУ и НП получаем характеристики преобразования, которые приведены на рис. 4 и 5
     

Рисунок 4 - Зависимость выходного напряжения ДУ от температуры

Рисунок 5 - Зависимость выходного напряжения НП от температуры

     Путем трансляции данных рассчитанной математической модели в EWB, получаем модель усилителя с измерительным мостом, которая приведена на рис. 6.

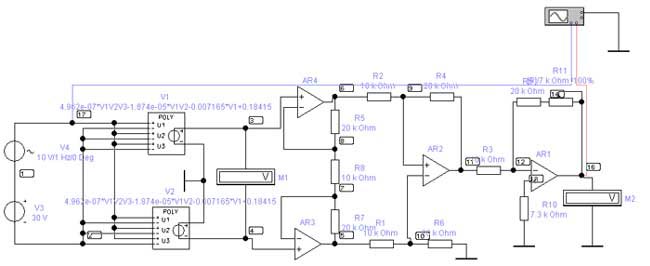
Рисунок 6 - Модель измерительного канала температуры

     Характеристики преобразования на выходах ДУ и НП, которые получены с учетом рассмотренной модели (рис. 6) в EWB 5.12 PRO приведены на рис. 7 и 8.

Рисунок 7 - Зависимость выходного напряжения ДУ в EWB 5.12 PRO от температуры

Рисунок 8 - Зависимость выходного напряжения НП в EWB 5.12 PRO от температуры

     В процессе имитационного моделирования измерительного канала температуры установлены значения чувствительности измерителя (0,14 В/°С и 0,4 В/°С на выходах ДУ и НП соответственно), произведен анализ переходных процессов, спектральный анализ, исследовано влияние температуры на аналоговые полупроводниковые элементы.
     Экспериментально установлено, что показатели точности при измерении температуры в полученных имитационных моделях, по сравнению с опытными образцами приборов не выходят за допустимые пределы. Так, относительная погрешность измерения температуры при имитационном моделировании и согласно экспериментальных данных лежит в диапазоне (0,5…1) %.

     Выводы.
     1. Разработана имитационная математическая модель измерителя, пригодная для дальнейшей алгоритмизации с реализацией в соответствующих пакетах прикладных программ.
     2. При сравнении рассчитанных характеристик преобразования в MathCad с полученными в результате моделирования в EWB 5.12 PRO установлено, что разработанные математические модели адекватны реальным измерительным каналам, с ошибкой, значение которой не превышает (0,5…1) %.
     3. Полученная имитационная модель измерительного канала температуры позволяет производить альтернативный выбор вариантов схемных решений и возможность подбора наиболее приемлемой элементной базы для различных измерительных каналов информационно-измерительных приборов и систем

Литература

     1. Сухоруков В.В. Неразрушающий контроль. – М: Высшая школа, 1991. – 283 с.

     2. Зорі А.А., Коренєв В.Д., Хламов М.Г. Електронні системи вимірювання і контролю параметрів водних середовищ. Навчальний посібник. – Донецьк: РВА ДонНТУ, 2002. –352 с.

© ДонНТУ, Соломичев Роман Игоревич, 2010