Главная страница ДонНТУ Портал магистров ДонНТУ

Автобиография Реферат Индивидуальный раздел Отчет о поиске Ссылки

Исследование затухания ультразвука в воздухе и структуре металла валков горячей прокатки из стали 150ХНМ

Зори А.А., Соломичев Р.И., Тарасюк В.П.

Донецкий национальный технический университет

Источник: Вестник НТУ "ХПИ". / Материалы научно-технической конференции. — Харьков, НТУ "ХПИ"— 2010, 380 с.

     Предложен расчет коэффициентов затухания ультразвука в металле бандажа валков из конкретного типа стали при изменении геометрических размеров зерен металла под действием температуры, а также определены коэффициенты затухания звуковой волны в воздухе при изменении расстояния от объекта контроля до преобразователя. Произведен подбор наиболее оптимальных параметров функционирования разрабатываемой электронной системы.

     In the work was taken the calculation results of the ultrasonic attenuation coefficients in the metal bandage rolls of a steel when the geometrical the grains dimensions of the metal under the temperature influence, as well as the damping coefficients of the sound wave in the air when changing the distance from the object to control the converter. Made to select the most optimal functioning parameters developed an electronic system.

     Введение. Остановка производства стального проката на металлургическом комбинате в связи с внезапным выходом из строя прокатных роликов влечет за собой значительные экономические последствия для предприятия. Поэтому, на данный момент перспективным направлением в металлургическом производстве является осуществление непрерывной оценки износа оборудования с помощью неразрушающего контроля (НК).
     В приповерхностном слое металла бандажа сталепрокатных валков в процессе многоразовой горячей прокатки возникают усталостные трещины под значительными нагрузками и перепадами температур, которые необходимо своевременно отследить на ранних стадиях их развития. Данная проблема решается бесконтактным электромагнитно-акустическим (ЭМА) методом неразрушающего контроля.
     Постановка задачи. Для разработки электронной системы диагностического контроля состояния валков, необходимо исследовать затухание ультразвуковых колебаний (УЗК), как в структуре металла, при изменении размеров зерен под действием температуры, так и в воздушной прослойке между датчиком и поверхностью валков.
     Решение задачи и результаты исследований. Коэффициент затухания УЗК δ складывается из коэффициентов поглощения δп и рассеяния δр: δ=δп+δр. При поглощении звуковая энергия переходит в тепловую, а при рассеянии энергия остается звуковой, но уходит из направленно распространяющейся волны. Большое влияние на величину коэффициента рассеяния δр в металле оказывает соотношение среднего размера кристаллов (зерен) - Dcp с длиной волны ультразвука - λ. При Dcp << λ коэффициент δр пропорционален f ^ 4, где f – частота колебаний (рис.1). Общее затухание в этом случае определяется формулой [1].

                                                      (1)

где А и В – постоянные,.

Рисунок 1 - Схематическая зависимость коэффициента затухания от среднего диаметра зерна и длины волны

     Расчет коэффициентов затухания производится при частоте колебаний f = 2,0 МГц. Зная скорость распространения волны в углеродистых сталях c1 = 5900 м/с, определим длину волны λ из соотношения:

                                             (2)

     При теоретическом расчете затухания УЗК в металле воспользуемся справочными данными [2] – характеристикой изменения средней величины зерна стали 150ХНМ от рабочей температуры валков (рис.2). При минимальной рабочей температуре T≈150 °C средний диаметр зерна составляет Dcp=0,0365 мм. Тогда, согласно выражению (1) получим затухание:

Или выразим в отрицательных децибелах, используя формулу:

                                                            (3)

где Х – удаление от источника УЗК, на котором вычисляется затухание.

Рисунок 2 - Изменение средней величины зерна в зависимости от температуры нагрева

     В таблице 1 представлены значения приведенных коэффициентов затухання наклонных поперечных ультразвуковых волн, определенные по формуле (1) при при Х: 16, 24 и 30 мм , а также значения, рассчитанные по формуле (3), где ΔN – разность показаний аттенюатора затухания ультразвука в дБ в объекте контроля (ОК) при прохождении расстояния Х=Х1+Х2 и изменении температуры на ΔT=50 °C (рис.3).

Таблица 1

Значения коэффициентов затухания УЗК в зависимости от размеров зерен металла

Dcp, мм	δ, 1/мм	X = 16 мм		X = 24 мм		X = 30 мм
		N, дБ	ΔN, дБ	N, дБ	ΔN, дБ	N, дБ	ΔN, дБ
0,033	0,0194	-2,7099	0	-4,0648	0	-5,081	0
0,037	0,0195	-2,7224	0,012	-4,0836	0,019	-5,1044	0,023
0,04	0,0197	-2,7386	0,029	-4,1079	0,043	-5,1349	0,054
0,044	0,0198	-2,7597	0,05	-4,1295	0,075	-5,1744	0,093
0,048	0,0200	-2,7871	0,077	-4,1807	0,116	-5,2259	0,145
0,052	0,0203	-2,8228	0,113	-4,2342	0,169	-5,2927	0,212
0,057	0,0206	-2,8692	0,159	-4,3038	0,239	-5,3797	0,299
0,062	0,0210	-2,9295	0,22	-4,3942	0,329	-5,4927	0,412
0,067	0,0216	-3,0079	0,298	-4,5118	0,447	-5,6397	0,559

Рисунок 3 - Схема проведения диагностического контроля

     На рис. 4 приведена зависимость ΔN от среднего диаметра зерна стали 150ХНМ на частоте 2,0 МГц при Х=16 мм (кривая 1), Х=24 мм (кривая 2) и Х=30 мм (кривая 3).

Рисунок 4 - Зависимость ΔN от среднего диаметра зерна стали 150ХНМ

     Из полученных результатов следует, что затухание волны в металлической структуре валков не превышает 1 дБ. В контексте проектируемой электронной системы диагностического контроля это показывает, что снижение амплитуды УЗК будет не существенным при изменении среднего диаметра зерен от 0,033 мм до 0,067 мм, вызванное изменением температуры  валков от 150 °C до 500 °C.
     Расчитаем коэффициент затухания акустической волны в воздушном слое, толщиной h (рис.3), который имеет место между ОК и приемником УЗК. Для этого составим волновое уравнение для вязкой теплопроводящей среды, используя уравнение непрерывности:

                                                            (4)

и уравнение Навье-Стокса:

                                         (5)

где (Па•с) и (Па•с)– коэффициенты сдвиговой и объемной вязкости; с0 – скорость звука.
     Из выражений (4) и (5), которые являются линеаризованными уравнениями гидродинамики для возмущений плотности ρ’ и колебательной скорости v, находим уравнение для колебательной скорости, предпологая, что волна распространяется по оси y:

                                         (6)

где .

     С учетом эффективного коэффициента вязкости получим:

                                             (7)

где k-коэффициент теплопроводности, его зависимость от температуры приведена на рис.5 [3]; (Дж/кг•К) и (Дж/кг•К)  - удельные теплоемкости при постоянном давлении и объеме.

Рисунок 5 - Зависимость коэффициента теплопроводности воздуха от температуры

     Ищем решение волнового уравнения (6) в виде:

                                                 (8)

     После подстановки в волновое уравнение получаем закон дисперсии:

                                             (9)

     Отсюда находим, что если (это соответствует малому затуханию звука на расстояниях порядка длины волны), то

                           (10)

     Используя выражение (8) при , имеем коэффициент затухания звука с учетом изменения температуры воздуха:

                           (11)

где с(Т)=331,3+1,21•Т -зависимость скорости звука от температуры воздуха [4] (рис.6), кг/м3 – плотность воздуха, ω=2πf – круговая частота в рад/с.

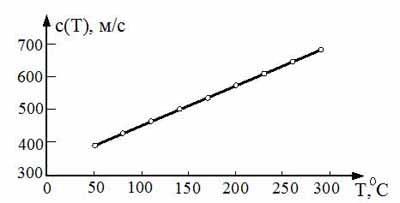
Рисунок 6 - Зависимость скорости звука в воздухе от температуры

     Согласно формуле (11), имеем зависимость коэффициента затухания УЗК в воздухе от изменения температуры воздуха от 50 °C до 300 °C (рис.7).

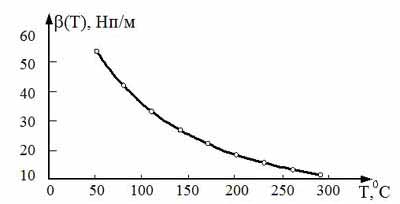
Рисунок 7 - Зависимость коэффициента затухания УЗК в воздухе от температуры

     Используем выражение (3), для выражения затухание в отрицательных дБ при вариации расстояния h от ОК до приемника УЗК. Результаты исследования привелены в таблице 2.

Таблица 2

Значения коэффициентов затухания УЗК в воздухе при изменении температуры

T, °C	β, 1/мм	X3 = 3 мм	X3 = 5 мм	X3 = 7 мм
		N, дБ	N, дБ	N, дБ
50	54,22	-1,413	-2,355	-3,297
80	42,20	-1,100	-1,833	-2,566
110	33,52	-0,874	-1,456	-2,038
140	27,12	-0,707	-1,178	-1,649
170	22,28	-0,581	-0,968	-1,355
200	18,56	-0,484	-0,806	-1,128
230	15,64	-0,408	-0,679	-0,951
260	13,32	-0,347	-0,579	-0,810
290	11,45	-0,298	-0,497	-0,696

     В таблице 2 представлены значения приведенных коэффициентов затухання наклонных поперечных ультразвуковых волн в воздушном слое, где N – затухания ультразвука в дБ между объектом контроля (ОК) и приемником при прохождении расстояния X3 (рис.3). На рис. 8 приведена зависимость N от температуры на частоте УЗК 2,0 МГц при X3=3 мм (кривая 1), при X3=5 мм (кривая 2) и при X3=7 мм (кривая 3).

Рисунок 8 - Зависимость ΔN от температуры воздуха и расстояния h

     Заключение. Из результатов исследования следует, что затухание волны в воздухе велико, существенно зависит от расстояния h и превышает затухание волны в металле больше чем в 2000  раз (по шкале в неперах, 1Нп=1 1/мм). Общий коэффициент затухания определяется как алгебраическая сумма коэффициентов затухания волны в двух средах. Основное снижение амплитуды УЗК в основном происходит из-за наявности воздушного слоя, который является неизбежным и необходимым условием безконтактного способа контроля валков и, следовательно, затуханием в металле можно пренебречь. Повышение амплитуды УЗК у приемника, не увеличивая мощности излучения, возможно лишь при уменьшении воздушного зазора, который является оптимальным в пределах X3=5 мм.

Литература

     1. Сухоруков В.В. Неразрушающий контроль. – М: Высшая школа, 1991. – 283 с.

     2. Геращенко О.А, Гордов А.Н, Лах В.И. Справочник: температурные измерения. – К: Наукова думка, 1984. – 495 с.

     3. Лепендин Л.Ф. Акустика. – М: Высшая школа, 1978. – 445с.

     4. Гурбатов С.Н, Руденко О.В. Акустика в задачах. – М: Наука, 1996.– 335 с.

© ДонНТУ, Соломичев Роман Игоревич, 2010