Введение
В настоящее время в Украине проблема газоснабжения городов стоит достаточно остро. Прогнозирование потребления и спроса на газ является основой не только
для планирования закупок природного газа у газотрейдеров, но, что не менее важно, для разработки мероприятий по управлению энергопотреблением в муниципальном хозяйстве, особенно в отопительный период.
Основной задачей является получение более точного прогноза на определенный период времени с учётом максимального количества факторов, влияющих на спрос природного газа. Недооценка нагрузки может привести к росту использования пикового объёма, что, в свою очередь, ведёт к снижению резервов, а завышенный прогноз нагрузки может привести к необоснованному увеличению резерва, и, следовательно, себестоимости газа. Поэтому очень важным является качество оперативного прогнозирования графика нагрузки сети.
Вверх
Актуальность темы
Актуальность прогнозирования баланса природного газа в разрезах времени на основе спроса и потребления несомненна, так как обоснованные прогнозы являются эффективным инструментом перспективного планировщика и управления в энергоотрасли. Актуальность исследований проявляется в применении полученных результатов для оперативного и тактического управления. Исследования в этой области ведутся многими специалистами предприятий газовой отрасли, а именно:
• Бархударян И.Г., Оганесян Л.А. – применение математических методов прогнозирования, построение моделей потребления природного газа ;
• Коваленко М.В., Махотило К.В. Вести - использование нейронных сетей при прогнозировании использования энергоресурсов;
• Рональд H. Браун, Брайен M. Маркс и Джордж Ф.Корлисс, а также С.Джил, Дж.Деферрари и др.
Вверх
Методология и методы исследований
Из существующих методов прогнозирования в области потребления энергоресурсов наиболее часто применяются статистические методы и методы эвристического прогнозирования.
Одним из распространенных способов построения вероятностных прогнозов является построение регрессионных зависимостей. Строятся, в основном, однопараметрические модели, где переменной является фактор времени. Такие модели часто называются динамическими; они более типичны для прогнозирования, так как здесь решается вопрос об изменении главного признака - времени в будущем.
Чтобы выявить некоторые закономерности изменения во времени, недостаточно определить только тенденцию. Для этого необходимо изучить внутреннюю структуру отклонений динамического ряда от найденной тенденции, используя корреляционный метод.
Отличительной чертой динамических рядов является наличие корреляции между соседними членами ряда. Однако методы корреляционного анализа основываются на предположении о независимости элементов статистического ряда. Поэтому для установления тесноты связи между уровнями ряда динамики определяется коэффициент автокорреляции.
Наиболее часто в рядах динамики встречается полиномиальная, экспоненциальная и гармоническая составляющая тренда. Наиболее пригодным для выделения тренда является метод скользящей средней.
1. Пользуются двумя модификациями метода скользящей средней: простое сглаживание основывается на составлении нового ряда из простых среднеарифметических, исчисленных для определенных промежутков времени;
2. взвешенное сглаживание состоит в определении взвешенных средних для равных точек ряда динамики.
Как правило, значения временного ряда из недалекого прошлого лучше описывают прогноз, чем более старые значения этого же ряда. Тогда можно использовать для прогнозирования скользящее среднее
Y(t+1)=(1/(T+1))*[Y(t)+Y(t-1)+...+Y(t-T)], (3.2)
Смысл его заключается в том, что модель видит только ближайшее прошлое (на T отсчетов по времени в глубину) и, основываясь только на этих данных, строит прогноз. При прогнозировании довольно часто используется метод экспоненциальных средних, который постоянно адаптируется к данным за счет новых значений.
Формула, описывающая эту модель, записывается как:
y(t+1)=a*y(t)+(1-a)* y^(t), (3.3)
где y(t+1) – прогноз на следующий период времени;
y(t) – реальное значение в момент времени t;
y^(t) – прошлый прогноз на момент времени t;
a – постоянная сглаживания (0<=a<=1)).
Наряду с описанными выше методами, основанными на экспоненциальном сглаживании, уже достаточно долгое время для прогнозирования используются регрессионные алгоритмы. Существует прогнозируемая переменная Y (зависимая переменная) и отобранный заранее комплект переменных, от которых она зависит - X1, X2, ..., XN (независимые переменные). Природа независимых переменных может быть различной. Главное - уметь формализовать все внешние факторы, от которых может зависеть уровень спроса в числовую форму.
При построении долгосрочных прогнозов используют более современные технологии прогнозирования, например: нейронные сети, генетические алгоритмы.
В исследуемой проблеме первоочередным является определение срока, на который делается прогноз.При этом существует следующая градация периодов:
1.краткосрочный - период упреждения от нескольких часов до месяца;
2.среднесрочный - от нескольких месяцев до года;
3.долгосрочный - от года до 5 лет и более.
Одной из наиболее сложных в методическом отношении является проблема долгосрочного прогнозирования. Сложность ее обусловлена объективно существующими трудностями учета качественных изменений объекта прогноза, достоверная и систематизированная информация о которых в ретроспективном периоде часто отсутствует.
Процесс решения задачи прогнозирования может быть рассмотрен как преобразование исходной информации, полученной путем сбора статистических данных или анализа результатов решения смежных задач. Статистические данные, характеризующие процесс газопотребления, образуют дискретные динамические ряда, получаемые регистрацией данных через определенный период (час, день, неделя, месяц, год).
Краткосрочный прогноз необходим в целях диспетчерского управления, где предвидение почасовых и ежесуточных потребностей в газе необходимо для рационального перераспределения потоков газа между потребителями в течение суток, месяца. Среднесрочные и долгосрочные прогнозы служат плановым разработкам с целью выявления общей тенденции развития системы газоснабжения рассматриваемого экономического района. Наиболее целесообразно применение в целях прогнозирования следующих методов:
* экстраполяции тенденций;
* моделирования;
* экспертных оценок.
Как показали исследования, суточный и годовой режимы газопотребления формируются: метеорологическими (текущие и предшествующие температуры наружного воздуха), астрономическими (смена дня и ночи, дней недели) режимными (степень загрузки и структура потребителей), общественными (социальный уклад населения) и другими факторами. Необходимость применения эвристического анализа обусловливается также наличием в исходной информации факторов, не поддающихся количественной оценке и относящихся по классификации типа информации к мнению.
При таком подходе к решению задачи устанавливаются количественные и качественные характеристики, отражающие специфику изучаемого процесса, на основе чего, подставляя нужные значения аргумента t, можно прогнозировать режимы и качественные изменения газопотребления.
Из современных методов построения прогноза я планирую использовать нейронные сети.
Выбор обусловлен такими преимуществами нейронных сетей:
* по сравнению с линейными методами статистики, нейронные сети позволяют эффективно строить нелинейные зависимости, более точно описывающие наборы данных;
* нейронная сеть же обучается на всей выборке данных, не фрагментируя её, что повышает адекватность настройки нейросети;
* нейронная сеть же создается путем указания вида структуры, числа слоев и числа нейронов в каждом слое. А алгоритмы построения растущих нейросетей и вовсе не требуют первоначального задания размера нейронной сети. Альтернативой нейронной сети при построении сложных нелинейных моделей является только метод группового учета аргументов (МГУА).
Вверх
На глобальном уровне:
Вопросы планирования и прогнозирования широко освещены в работах современных зарубежных
авторов Рональд H. Браун, Брайен M. Маркс и Джордж Ф.Корлисс,С.Джил, Дж.Деферрари, Р. Акоффа, И. Ансоффа, Г. Бенвенисте, Л. Фогеля, Дж. Бигеля, Г. Вейе, Ч. Ганнта, П. Дракера, У. Деринга, М. Портера,
Ф. Тейлора, А. Файоля, Р. Фалмера, Г. Форда, и других.
А точнее:
1. Ronald H. Brown, Brian M. Marx, and George F. Corliss "Mathematical Models for Gas Forecasting"
2. S.Gil, J.Deferrari. "Generalized Model of prediction of Natural Gas Consumption"
Вверх
Описание разрабатываемой подсистемы
Для построения модели были использованы данные по потреблению газа, предоставленные Харцызским управлением по газоснабжению и газификации. Данные представляют собой значения ежемесячного потребления газа городом за период 1998-2009гг., то есть за 12 лет, что позволит в дальнейшем реализовать долгосрочный прогноз.
Постановка задачи:
Заданы дискретные отсчеты {y(t1), y(t2)..., y(tn)} в последовательные моменты времени t1, t2,..., tn. Задача прогнозирования заключается в предсказании значения y(tn+1) в некоторый будущий момент времени tn+1.
Для решения задачи будем использовать математический аппарат искусственных нейронных сетей.
Для этого необходимо:
1. сформировать обучающую выборку;
2. выбрать конфигурацию нейронной сети;
3. обучить нейронную сеть;
4. протестировать нейронную сеть.
Общий механизм работы подсистемы прогнозирования потребления природного газа представлен на рис.1

Рисунок 1 – Механизм работы подсистемы прогнозирования потребления природного газа
(Анимация: объём – 56,011 КБ; размер – 336х280; количество кадров – 6; задержка между кадрами – 1000 мс; задержка между последним и первым кадрами – 1000 мс; количество циклов повторения – непрерывный цикл повторения)
Формирование обучающей выборки:
Имеющиеся данные потребления газа представляют собой упорядоченную во времени последовательность, то есть временной ряд. С целью определения зависимости между наблюдениями (разделенными временными интервалами в один месяц), вычислялся коэффициент автокорреляции, который отражает, в сущности, обычную корреляцию, вычисляемую между образующими временной ряд текущими и запаздывающими значениями зависимой переменной. С помощью корреляционного анализа установлено, что существует зависимость прогнозируемой величины от значения в предыдущий момент времени (месяц) и от такого же месяца годом ранее. Таким образом, выбраны следующие значения временного ряда: y(tn-1) и y(tn-13) в качестве входных факторов.
Так же исследования показали влияние усредненного значения потребления газа за прогнозируемый месяц и предыдущий, это величина также включена в входной набор данных.
Нормировка данных позволяет привести разнородные данные к сопоставимым диапазонам, а также приблизить их распределение к равномерному, что повышает информативность обучающего примера. Из возможных вариантов нормировки был выбран следующая линейная нормировка, которая приводит все значения к единому диапазону [0,1] [3].
Таким образом, все значения временного ряда были нормированы и на вход нейронной сети подаются только значения в диапазоне [0,1]. [3].
Выбор архитектуры нейронной сети:
Для решения задач прогнозирования больше всего подходят следующие виды нейронных сетей: многослойный персептрон (MLPсеть) и радиально-базисная сеть (RBFсеть).[4]
Но в большинстве случае при решении одной и той же задачи размер сети RBF будет превышать размер MLP. Сеть RBF имеет в своем составе один скрытый уровень, а сеть MLP в общем случае – несколько. Однако [5] любая функция может быть аппроксимирована трехслойной сетью MLP c одним скрытым слоем с любой степенью точности. При этом применение большего количества уровней является нецелесообразным, так как при этом время обучения увеличивается, а точность прогноза уменьшается. Таким образом, задача выбора числа слоев для обоих типов нейросетей не стоит: как сеть RbF, так и сеть MLp должны иметь один скрытый слой.
Сети RBF позволяют использовать лишь гауссову функцию активации, либо ее модификации. В тоже время MLP обладает способностью работать с различными функциями, что дает более широкие возможности для экспериментирования в процессе построения нейросетевой модели.
Кроме того, сеть RBF не обладает способностью к экстраполяции данных при увеличении ширины диапазона значений входных данных, так как отклик сети быстро затухает при удалении от сформированных на обучающей выборке центров классов.
Недостатком сети MLP по сравнению с RBF является более высокая сложность обучения ввиду необходимости совместного обучения нескольких слоев нейронов.
Таким образом, в качестве базовой сети была выбрана MLP-сеть. В качестве инструментальной среды использовался пакет Mathlab 7.0 (neural network toolbox). Проведены эксперименты, в результате которых выбрана следующая архитектура нейронной сети, состоящая из входного слоя, скрытого слоя, состоящего из 7 нейронов и выходного слоя (рис. 2). Используются следующие функции активации: на скрытом слое - гиперболический тангенс, на выходном - линейная.

Рисунок 2 - Архитектура нейронной сети.
Обучение и тестирование нейронной сети:
Сеть обучается алгоритмом обратного распространения ошибки. Среда Mathlab 7.0 позволяет использовать различные его модификации. К примеру, такие алгоритмы второго порядка, как метод сопряженных градиентов и метод Левенберга-Марквардта, который является наиболее распространенным алгоритмом оптимизации. [6,7]. Он превосходит по производительности метод наискорейшего спуска и другие методы сопряженных градиентов, а в некоторых задачах работает существенно быстрее, даже чем простейший градиентный метод. Превосходство данного метода, было подтверждено экспериментально.
Исходная обучающая выборка разделена на подмножество для обучения и проверочное подмножество, которое используется для проверки эффективности работы обученной сети.
Вверх
Описание полученных и планируемых результатов
Предоставленная за 12 лет информация использована следующим образом: данные потребления газа за 11 лет включены в обучающую выборку, а за последний (12) год - в проверочную. После обучения нейронной сети выполнено ее тестирование. Результаты тестирования представлены на рис. 3. На первой половине рис. 3 представлены результаты тестирования на обучающей выборке, а на второй - проверочной. Среднеквадратичная ошибка на проверочной выборке равна 6.1579e-004. Следует отметить, что прогноз на первые три месяца выполнен существенно точнее, чем на год.
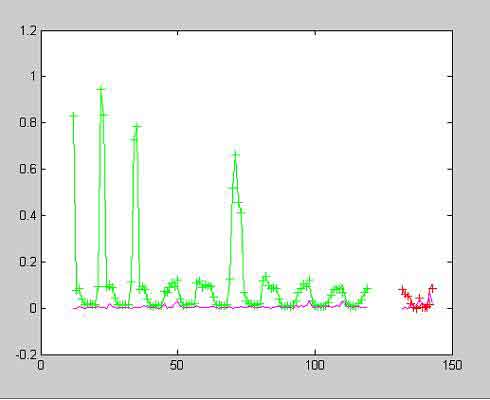
Рисунок 3 - Тестирование нейронной сети.
Вверх