РАЗРАБОТКА ЭКСПЕРТНОЙ СИСТЕМЫ АНАЛИЗА СЛАБОСТРУКТУРИРОВАННЫХ ПРОБЛЕМНЫХ СИТУАЦИЙ В ОРГАНИЗАЦИОННЫХ СИСТЕМАХ С ПРИМЕНЕНИЕМ НЕЧЕТКИХ КОГНИТИВНЫХ КАРТ
Андрейченко А. Н., Секирин А. И.
Донецкий Национальный Технический Университет г. Донецк
Кафедра автоматизированных систем управления
Источник: Сборник материалов I всеукраинской научно-технической конференции студентов, аспирантов и молодых ученых «Комп'ютерний моніторінг та інформаційні технології (ИУС и КМ - 2010)». II том. Донецк, ДонНТУ - 2010. с. 96-100.
Андрейченко А. Н., Секирин А. И. Разработка экспертной системы анализа слабоструктурированных проблемных ситуаций в организационных системах с применением нечетких когнитивных карт. В статье рассматривается вопрос применения нечетких когнитивных карт для анализа слабоструктурированных проблемных ситуаций в организационных системах и получения прогноза целевых показателей.
Общая постановка проблемы. Выживаемость и успешное развитие организационных систем (организаций) в условиях неопределенности будущего (социальной, экономической, политической, экологической нестабильности, жесткой конкуренции) зависит от способности менеджмента предвидеть возможные тенденции изменения ситуации и формировать соответствующие стратегии развития организации. Ярким примером реализации такой идеологии является сбалансированная система показателей (ССП), получившая широкую известность в последнее десятилетие. ССП ориентирована на выявление стратегических факторов - целей и показателей деятельности, принадлежащих четырем группам: финансовой, клиентской, внутренних бизнес-процессов, обучения и развития персонала, а также на установление причинно-следственных связей между ними.
Постановка задачи исследования. На сегодняшний день, известен ряд формальных (математических) моделей и методов описания и анализа развития слабоструктурированных проблемных ситуаций с учетом человеческого фактора. В данной работе необходимо исследовать возможность применения таких методов для конкретных задач. Для этого требуется решить две главные задачи:
анализ суммарных взаимных влияний факторов, как непосредственных, так и опосредованных через промежуточные факторы (статический анализ);
анализ возможных изменений стратегических факторов системы на временном интервале моделирования (динамический анализ).
Решение задачи и результаты исследования. Были рассмотрены аналогичные системы (ARIS BSC, Oracle Hyperion Performance Scorecard, система сбалансированных показателей UPE от Soft Prom и т. д.). Они не подходят для решения задачи в полном объеме, а также не обеспечивают достаточную точность результатов при наличии в системе слабоструктурированных ситуаций. Для решения поставленной задачи был проведен выбор математических методов и моделей. В результате решено использовать нечеткие когнитивные карты (НКК), предложенные Коско, а также различные математические методы позволяющие анализировать организационные системы в условиях неопределенности и слабой структурированности. Для анализа суммарных взаимных влияний факторов, как непосредственных, так и опосредованных через промежуточные факторы применяются специальные формулы, использующие НКК, матрицы связей и операции интервальной амбивалентной логики. Для анализа возможных изменений стратегических факторов системы на временном интервале моделирования применяется триадная модель. Триадная модель состоит из трех блоков: операционного, целевого и оценочного. Операционный блок включает в себя индикативные логические функции, событийную сеть Петри (граф операций) и лицо, принимающее решение, которое для операций процесса задает величину приращений индикаторов целей и показателей деятельности. Целевой блок состоит из событийной сети Петри, моделирующей достижение промежуточных целей, и графа приращений индикаторов конечных целей. Оценочный блок представляет собой граф приращений показателей деятельности.
На сегодняшний день существует ряд научных разработок в области анализа слабоструктурированных ситуаций в организационных системах. Слабая структурированность ситуации (соответственно, нечеткость когнитивной карты) согласно О. П. Кузнецову и его соавторам [3] характеризуется тем, что:
состав факторов и связей не определен с достаточной полнотой и доопределяется в процессе анализа ситуации;
значения факторов и связей являются качественными (не количественными) и выражаются либо вербальными (лингвистическими) оценками (типа "слабый", "средний", "сильный"), либо интервалами на числовой оси, либо нечеткими величинами с некоторой степенью вероятности. Качественные значения изменяются на линейно упорядоченной шкале;
оценки факторов и связей формируются на основе опроса экспертов и потому являются субъективными.
В монографии В.В. Кульбы и его соавторов [4] ситуации подразделены на стандартные (анализируются на основе заранее выработанных правил и процедур), хорошо структурированные (отсутствие неопределенности, многовариантность решений и применение оптимизационных методов), слабоструктурированные (применяется когнитивный анализ, а также методы исследования операций, теории игр, имитационного моделирования), неструктурированные (высокая степень неопределенности, невозможность формализации, анализируются на основе опыта и интуиции специалистов).
Строго говоря, такая классификация несколько условна. Реально сложная организация (корпорация) отображается совокупностью взаимосвязанных субмоделей, которые могут соответствовать ситуациям разного типа. Примером такой комбинированной модели, частично хорошо и частично слабоструктурированной, адекватно отображающей динамику развития ССП, является так называемая "триадная" модель [7].
Рассмотрим алгоритм выполнения статического анализа слабоструктурированных ситуаций в организационных системах. Взаимовлияния факторов вычисляются по НКК следующим образом:
- опосредованное влияние Ip, фактора Вi на фактор Вj через путь Р, ведущий из i в j
 |
(1) |
где Е(Р) - множество дуг пути P, Wkl - вес дуги (k, l) в пути Р;
- суммарное (интегральное) влияние Tij i на j по всем путям P(i,j), ведущим из i в j
Проиллюстрируем выражения (1) и (2) на примере НКК, для которой граф G, матрица W связей и матрица W± удвоенной размерности с неотрицательными весами даны на рис. 1. Рассмотрим влияние фактора 4 на фактор 2. Из 4 в 2 ведут три пути, для которых I(4,2) = -0,4; I(4,3,2) = min{0,5; -0,6} = -0,6; I(4,1,2) = min{0,5; 0,3} = 0,3. Таким образом, T42 = max{-0,4; -0,6; 0,3} = 0,3.

Рисунок 1. Пример графа G и матриц W, W± НКК
 |
(2) |
Структура триадной модели дана на рис. 3, где {vi} -множество внешних воздействий на операционный блок; {ci},{Δci} - множество индикаторов целей и приращений индикаторов целей, соответственно; {di},{Δdi} - множество показателей деятельности и их приращений, соответственно; качественные переменные {ci},{di}, а также их приращения {Δci},{Δdi} определены на количественной (балльной) шкале; {pi} - множество операций процесса, реализуемого в организационной системе; {fi} - множество событий, инициирующих переходы между операциями, описываются индикативными логическими функциями [14, 17]; ЛПР - лицо, принимающее решение, которое для операций процесса задает величину приращений (положительных или отрицательных) индикаторов целей и показателей деятельности.
Событийную сеть Петри (граф операций [15]) определим как набор S = <N, Φ, α>, где N=<P, T, E, M0> - сеть Петри [18]; Р= {pi|i=1,...,n} - множество позиций сети, которые в операционном блоке соответствуют операциям процесса, а в целевом блоке - главной и промежуточным целям; T={ti|i=1,...,m} – множество переходов между позициями; E⊆(P*T)∪(T*P) - множество дуг; M0 - начальная маркировка сети; Φ={fi|i=1,...,r} - множество индикативных логических функций (событий), которые выражаются формулами, составленными из термов вида(x#γ), где х - числовая переменная, x∈(pi,ci,vi,di) (рис. 5.4); γ - константа; # - знак сравнения, #∈{=,≠,>,≥,<,≤}, с помощью логических связок AND(∧),OR(∨),NEG( ); α: T→Φ - функция "нагружения" переходов сети Петри функциями fi.
); α: T→Φ - функция "нагружения" переходов сети Петри функциями fi.
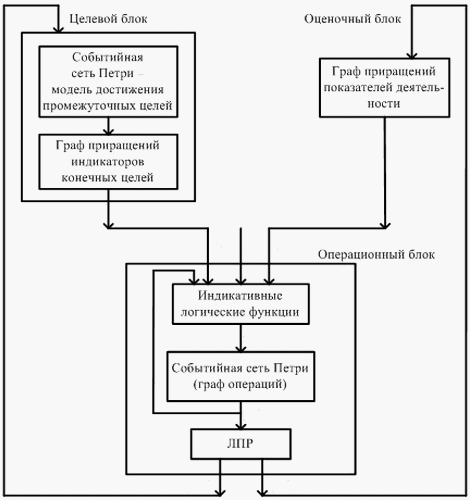
Рисунок 3. Структура триадной модели
1. Юдицкий С. А., Мурадян И. А., Желтова Л. В. Анализ слабоструктурированных проблемных ситуаций в организационных системах с применением нечетких когнитивных карт// Приборы и системы. Управление, контроль, диагностика. 2007. № 7.
2. Kaплан P.С. Нортон Д. П. Сбалансированная система показателей. От стратегии к действию // Пер. с англ. М.: ЗАО "Олимп-Бизнес", 2003.
3. Робертс Ф.С. Дискретные математические модели с приложением к социальным, биологическим и экономическим задачам / Пер. с англ. М.: Наука, 1986.
4. Силов В.Б. Принятие стратегических решений в нечеткой обстановке. М.: Инпро-РЕС, 1995.
5. Кузнецов О.П., Кулинич А.А., Марковский А.В. Анализ влияний при управлении слабоструктурированными ситуациями на основе когнитивных карт // Человеческий фактор в управлении / Под ред. Н. А. Абрамовой, К.С. Гинсберга, Д.А. Новикова. М.: КомКиига, 2006.
6. Кульба В.В., Кононов Д.А., Косяченко С.А., Шубин А.Н. Методы формирования сценариев развития социально-экономических систем. М.: Синтег, 2004.
7. Максимов В.И. Структурно-целевой анализ развития социально-экономических ситуаций // Проблемы управления. 2005. № 3.
8. Kosko В, Fuzzy Cognitive Maps// International Journal of Man-Machine Studies. 1986. № 24.
9. Liu Z.-Q., Zhang J.Y. Interrogating the structure of fuzzy cognitive maps // Soft Computing. 2003. V.7.
10. Юдицкий С.А., Желтова Л.В., Мурадян И.А. Моделирование динамики развития конфигураций организационных систем на основе сетей Петри и графов приращений // Проблемы управления. 2007. № 6.
11. Корноушенко Е.К. Максимов В.И. Управление ситуацией с использованием структурных свойств её когнитивной карты // Тр. ИПУ РАН. 2000. T.XI.
12. Zhang W.R.. Chen S.S., Chen K.N. et al. On NPN logic. Proc. 18th IEЕЕ Internat. Symp. MVL, Palma de Mollora, Spain, 1988.
13. Zhang W.R., Chen S.S., Bezdek J.C. Pool2: A Generic System for Cognitive Map Development and Decision Analysis// IEEE Transactions On systems, Man, and Cybernetics. 1989. V.19. № 1.
14. Владиславлев П.Н., Мурадян И.А., Юдицкий С.А. Взаимодействие целевой и операционной динамических моделей сложных процессов // Автоматика и телемеханика. 2005. №11.
15. Юдицкий С.А. Моделирование динамики развития организационных систем // Автоматика и телемеханика. 2008. № 1.
16. Юдицкий С.А., Магергут В.З. Логическое управление дискретными процессами. М.: Машиностроение, 1987.
17. Юдицкий С.А, Радченко Е.Г. Алгебра потокособытий и сети Петри - язык потокового моделирования многоагентных иерархических систем // Приборы и системы. Управление, контроль, диагностика. 2004. № 9.
18. Питерсон Дж. Теория сетей Петри и моделирование систем / Пер с англ. М.: Мир, 1984.
19. Юдицкий С.А., Владиславлев П. Н. Основы предпроектного анализа организационных систем. М.: Финансы и статистика, 2005.
В начало страницы >