Модель Леонтьева «Затраты-выпуск»
Подставляя технологические коэффициенты 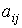 в (6.1.1), для каждой отрасли получаем балансовое соотношение
в (6.1.1), для каждой отрасли получаем балансовое соотношение

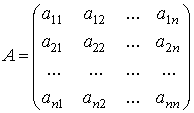

Уравнение (6.2.1), где A - постоянная технологическая матрица, 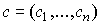 - известный вектор спроса,
- известный вектор спроса, 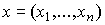 - неизвестный вектор выпуска, называется моделью Леонтьева. Интерпретируя выражение Ax как затраты, эту систему часто называют моделью «Затраты-выпуск».
- неизвестный вектор выпуска, называется моделью Леонтьева. Интерпретируя выражение Ax как затраты, эту систему часто называют моделью «Затраты-выпуск».
Модель Леонтьева призвана ответить на вопрос: можно ли в условиях данной технологии удовлетворить конечный спрос? Ответ на этот вопрос сводится к существованию решения системы

 . Условия существования и единственности решения такой системы хорошо известны из курса алгебры. Однако здесь речь идет о решении этой системы, имеющем подходящий экономический смысл. А именно, все элементы модели Леонтьева по их определению являются неотрицательными величинами, в том числе переменные
. Условия существования и единственности решения такой системы хорошо известны из курса алгебры. Однако здесь речь идет о решении этой системы, имеющем подходящий экономический смысл. А именно, все элементы модели Леонтьева по их определению являются неотрицательными величинами, в том числе переменные 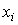 . Поэтому мы должны говорить о существовании неотрицательных решений системы (6.2.1).
. Поэтому мы должны говорить о существовании неотрицательных решений системы (6.2.1).
Определение 6.1. Модель Леонтьева называется продуктивной, если система (6.2.1) имеет неотрицательное решение  ,
, 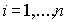 .
.
Перепишем систему (6.2.1) в виде  . Тогда
. Тогда 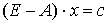 или
или

 -матрица. Теперь видно, что существование неотрицательного решения системы (6.2.1) определяется существованием невырожденной матрицы
-матрица. Теперь видно, что существование неотрицательного решения системы (6.2.1) определяется существованием невырожденной матрицы  , обратной к матрице
, обратной к матрице  .
.
Напомним, что матрица  называется невырожденной, если она имеет обратную матрицу
называется невырожденной, если она имеет обратную матрицу 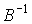 , определяемую условиями
, определяемую условиями 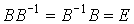 . Матрица B является невырожденной в том и только в том случае, если
. Матрица B является невырожденной в том и только в том случае, если 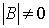 , где
, где  - детерминант (определитель) матрицы B. Обратная матрица
- детерминант (определитель) матрицы B. Обратная матрица 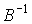 существует и неотрицательна, если все главные миноры матрицы B положительны (условие Хокинса-Саймона):
существует и неотрицательна, если все главные миноры матрицы B положительны (условие Хокинса-Саймона):
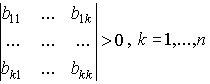
Для того чтобы применить эти условия существования и невырожденности к матрице  , приведем ряд дополнительных построений.
, приведем ряд дополнительных построений.
Система (6.2.1) является частным случаем (при 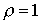 ) более общей системы
) более общей системы

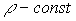 . Рассмотрим следующую, связанную с уравнением (6.2.3), систему
. Рассмотрим следующую, связанную с уравнением (6.2.3), систему 
 -матрица с элементами
-матрица с элементами 
Если 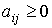 для всех i,j , то систему (6.2.3) можно преобразовать в (6.2.4) , положив
для всех i,j , то систему (6.2.3) можно преобразовать в (6.2.4) , положив 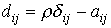 , где
, где  - символ Кронекера. Обратно, система (6.2.4) может быть преобразована в (6.2.3) . Для этого нужно взять достаточно большое положительное число
- символ Кронекера. Обратно, система (6.2.4) может быть преобразована в (6.2.3) . Для этого нужно взять достаточно большое положительное число  (
( 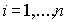 ) и положить
) и положить 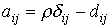 . Отсюда
. Отсюда 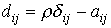 , причем
, причем 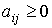 .
.
Следовательно, если мы найдем условия существования неотрицательного решения системы (6.2.4) , то тем самым докажем продуктивность модели Леонтьева, получаемой из (6.2.3) при 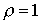 .
.
Справедливы следующие утверждения.
Теорема 6.1. Матрица D системы (6.2.4) , элементы которой удовлетворяют условиям (6.2.5) , неотрицательно обратима тогда и только тогда, когда уравнение (6.2.4) имеет неотрицательное решение (т.е. продуктивно).
(Квадратная матрица D называется неотрицательно обратимой, если она невырожденна и ее обратная матрица 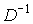 неотрицательна).
неотрицательна).
Теорема 6.2. Уравнение (6.2.4) продуктивно тогда и только тогда, когда матрица удовлетворяет условию Хокинса-Саймона, т.е. все главные ее миноры положительны.
Из приведенных утверждений следует, что необходимым и достаточным условием продуктивности модели Леонтьева (6.2.1) является существование неотрицательно обратимой матрицы  , т.е. чтобы матрица
, т.е. чтобы матрица  была невырожденна (
была невырожденна ( 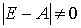 ) и чтобы обратная матрица
) и чтобы обратная матрица  была неотрицательна.
была неотрицательна.
Итак, если эти условия выполнены, то искомый вектор выпуска x определяется по формуле (6.2.2) . Матрица  предоставляет информацию о том, каким образом вектор конечного спроса c пересчитывается в необходимый вектор валового выпуска x. Из линейности модели Леонтьева по x и c следует, что приращение
предоставляет информацию о том, каким образом вектор конечного спроса c пересчитывается в необходимый вектор валового выпуска x. Из линейности модели Леонтьева по x и c следует, что приращение 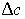 вектора c и соответствующее приращение
вектора c и соответствующее приращение 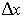 вектора x связаны между собой уравнением
вектора x связаны между собой уравнением 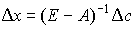 . Следовательно, матрица
. Следовательно, матрица  позволяет вычислить изменение валового выпуска, вызванное изменением конечного потребления. Поэтому матрицу
позволяет вычислить изменение валового выпуска, вызванное изменением конечного потребления. Поэтому матрицу  часто называют матричным мультипликатором. Элемент матричного мультипликатора
часто называют матричным мультипликатором. Элемент матричного мультипликатора  (обозначим через
(обозначим через  ) можно интерпретировать как количество продукта одного вида, необходимое для выпуска одной единицы продукции другого вида.
) можно интерпретировать как количество продукта одного вида, необходимое для выпуска одной единицы продукции другого вида.
Известно, что матрицу  можно представить в виде степенного ряда матриц:
можно представить в виде степенного ряда матриц:
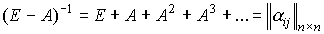
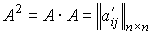 ,
, 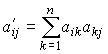 ,
,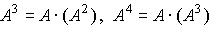 и т.д. Видим, что вычисление (аппроксимация) обратной матрицы
и т.д. Видим, что вычисление (аппроксимация) обратной матрицы  связано со сходимостью бесконечного степенного ряда
связано со сходимостью бесконечного степенного ряда 
Если матрица  неотрицательно обратима, то ряд (6.2.6) сходится, т.е. сумма (6.2.6) конечна и равна
неотрицательно обратима, то ряд (6.2.6) сходится, т.е. сумма (6.2.6) конечна и равна  .
.
Подытоживая сказанное, мы можем утверждать, что для продуктивной модели Леонтьева вектор валового выпуска x представляется матричным рядом

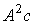 , ... интерпретируются как промежуточные затраты, а именно, Ac - затраты, необходимые для производства (выпуска) c ,
, ... интерпретируются как промежуточные затраты, а именно, Ac - затраты, необходимые для производства (выпуска) c , 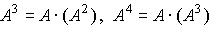 - затраты, необходимые для производства (выпуска) Ac и т.д. Содержательный смысл этой последовательности таков: для того чтобы получить чистый выпуск c , нужно затратить вектор продуктов Ac; затем, чтобы произвести в системе этот набор продуктов Ac , придется дополнительно затратить
- затраты, необходимые для производства (выпуска) Ac и т.д. Содержательный смысл этой последовательности таков: для того чтобы получить чистый выпуск c , нужно затратить вектор продуктов Ac; затем, чтобы произвести в системе этот набор продуктов Ac , придется дополнительно затратить 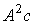 и т.д. Сумма вектора чистого выпуска c (вектора конечного потребления) и всех векторов промежуточных затрат (производственного потребления) и составляет вектор валового выпуска. Из предыдущего равенства следует, что решение уравнения (6.2.1) можно получить итерационно по формуле
и т.д. Сумма вектора чистого выпуска c (вектора конечного потребления) и всех векторов промежуточных затрат (производственного потребления) и составляет вектор валового выпуска. Из предыдущего равенства следует, что решение уравнения (6.2.1) можно получить итерационно по формуле
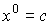 .
.
Важным следствием модели Леонтьева являются результаты, получаемые с применением двойственной к ней модели

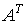 - транспонированная матрица A . Уравнению (6.2.7) можно придать смысловую стоимостную окраску. Действительно,
- транспонированная матрица A . Уравнению (6.2.7) можно придать смысловую стоимостную окраску. Действительно, 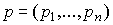 можно интерпретировать как вектор цен продуктов отраслей,
можно интерпретировать как вектор цен продуктов отраслей, 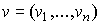 - как вектор добавленной стоимости (т.е. прибавка к стоимости товара после ее производства) на единицу выпуска,
- как вектор добавленной стоимости (т.е. прибавка к стоимости товара после ее производства) на единицу выпуска,  - как вектор суммы издержек на единицу выпуска. Тогда разность
- как вектор суммы издержек на единицу выпуска. Тогда разность 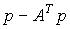 есть вектор чистого дохода от единицы выпуска. Этот чистый доход и приравнивается добавленной стоимости
есть вектор чистого дохода от единицы выпуска. Этот чистый доход и приравнивается добавленной стоимости  .
.
Существование решения двойственного уравнения (6.2.7) относительно вектора цен связано опять с неотрицательностью всех его элементов.
Если уравнение (6.2.7) имеет неотрицательное решение 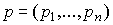 , то двойственная модель Леонтьева называется прибыльной. Это свойство является двойственным к понятию продуктивности модели Леонтьева в том смысле, что выполнение одного из свойств влечет справедливость другого. Данное положение является следствием наличия тесной математической связи между взаимно двойственными уравнениями (6.2.1) и (6.2.7) . Действительно, рассмотрим "двойственные" к (6.2.3) и (6.2.4) уравнения
, то двойственная модель Леонтьева называется прибыльной. Это свойство является двойственным к понятию продуктивности модели Леонтьева в том смысле, что выполнение одного из свойств влечет справедливость другого. Данное положение является следствием наличия тесной математической связи между взаимно двойственными уравнениями (6.2.1) и (6.2.7) . Действительно, рассмотрим "двойственные" к (6.2.3) и (6.2.4) уравнения

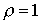 ) уравнения (6.2.8) , а (6.2.8) и (6.2.9) , как и (6.2.3) и (6.2.4) , взаимно преобразуемы друг в друга. Тогда для матрицы
) уравнения (6.2.8) , а (6.2.8) и (6.2.9) , как и (6.2.3) и (6.2.4) , взаимно преобразуемы друг в друга. Тогда для матрицы  справедливы утверждения, аналогичные теоремам 6.1 и 6.2, а также следующая теорема.
справедливы утверждения, аналогичные теоремам 6.1 и 6.2, а также следующая теорема.
Теорема 6.3. Для того чтобы модель Леонтьева (6.2.1) была продуктивной, необходимо и достаточно, чтобы двойственная к ней модель (6.2.7) была прибыльной.
Мы здесь рассмотрели классическую (исходную) модель Леонтьева, которая описывает производство по схеме затраты-выпуск. Значимость модели Леонтьева заключается еще и в том, что она применяется для описания ряда других экономических задач, а также служит отправной точкой для различных обобщений. В качестве подтверждения этого приведем интерпретацию уравнения (6.2.1) как модели международной торговли и модификацию модели Леонтьева как оптимизационной задачи.
При трактовке уравнения (6.2.1) как модели торговли n означает число торгующих между собой стран, 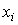 - национальный доход i-ой страны,
- национальный доход i-ой страны,  - национальные расходы i -ой страны,
- национальные расходы i -ой страны, 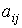 - объем импорта из страны i в страну j , приходящийся на одну единицу национального дохода страны j. Элементу
- объем импорта из страны i в страну j , приходящийся на одну единицу национального дохода страны j. Элементу  придается смысл коэффициента внутреннего потребления своей продукции i -ой страной.
придается смысл коэффициента внутреннего потребления своей продукции i -ой страной.
И в такой интерпретации, очевидно, все элементы модели Леонтьева должны быть неотрицательными и, более того, национальный доход и национальные затраты всегда являются положительными величинами. В данном случае модель (6.2.1) дает ответ на вопрос: каковы должны быть объемы национальных доходов стран, обеспечивающие стабильный уровень национальных расходов и установившийся режим обмена товарами между странами?
Выше было замечено, что одним из существенных упрощений модели Леонтьева является отсутствие в ней первичных (невозобновляемых) факторов производства. Модель будет более близкой к реальности, если наряду с воспроизводимыми (вторичными) ресурсами, описываемыми в (6.2.1) произведением Ax, будут учтены и первичные факторы. Оказывается, такое обобщение превращает модель Леонтьева в оптимизационную задачу.
Предположим, что в модели (6.2.1) каждый товар производится с использованием продукций всех отраслей и еще m видов первичных ресурсов. Обозначим через 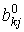 количество k-го первичного фактора, затрачиваемого в производство xj количества j-го товара, а через
количество k-го первичного фактора, затрачиваемого в производство xj количества j-го товара, а через 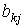 - количество k -го первичного фактора, необходимое для производства одной единицы товара вида j . Из определения этих величин следует, что, как и в случае вторичных ресурсов, имеет место выражение
- количество k -го первичного фактора, необходимое для производства одной единицы товара вида j . Из определения этих величин следует, что, как и в случае вторичных ресурсов, имеет место выражение 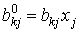 .
.
Таким образом, для каждого товара j мы имеем n+m видов представления его выпускаемого объема:
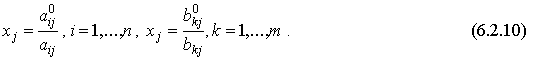

 ).
).
Как следует из (6.2.10) и (6.2.11) , для любых i и k


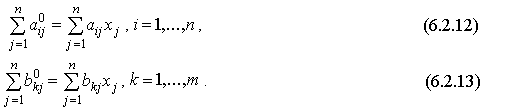
Так как уравнения (6.2.12) относятся к товарам каждой отрасли, используемым как на производственное, так и на конечное потребление, должно быть
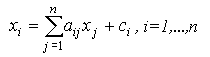
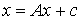 .
.
Введем в рассмотрение матрицу

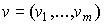 запасов всех первичных ресурсов, т.е.
запасов всех первичных ресурсов, т.е. 
 .
.
Обозначим через 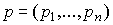 и
и 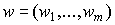 векторы цен вторичных и первичных ресурсов соответственно.
векторы цен вторичных и первичных ресурсов соответственно.
Поставим следующий вопрос: при каком векторе выпуска 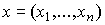 реализация конечного продукта
реализация конечного продукта 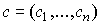 приведет к максимальному доходу с учетом наличного запаса
приведет к максимальному доходу с учетом наличного запаса 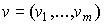 первичных ресурсов? В ответ получаем следующую задачу линейного программирования:
первичных ресурсов? В ответ получаем следующую задачу линейного программирования:


По правилам, приведенным в §2.4 (см. (2.4.2) и (2.4.4)), напишем для (6.2.14)-(6.2.15) двойственную задачу с новой переменной 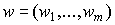 :
:

Введем изменение масштаба цен  и запишем двойственные задачи (6.2.14)-(6.2.15) и (6.2.16)-(6.2.17) в более компактном виде:
и запишем двойственные задачи (6.2.14)-(6.2.15) и (6.2.16)-(6.2.17) в более компактном виде:
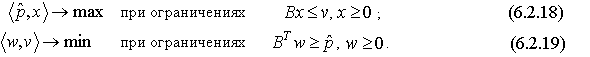
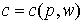 , а решение задачи (6.2.19) - вектор предложения первичных факторов
, а решение задачи (6.2.19) - вектор предложения первичных факторов 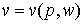 . Для пары задач (6.2.18) и (6.2.19) и их решений c и v верны все утверждения из §2.4 для двойственных задач линейного программирования.
. Для пары задач (6.2.18) и (6.2.19) и их решений c и v верны все утверждения из §2.4 для двойственных задач линейного программирования.
Согласно общего определения равновесия (см. §5.3), набор 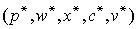 будет равновесным в модели Леонтьева, если выполнены соотношения
будет равновесным в модели Леонтьева, если выполнены соотношения
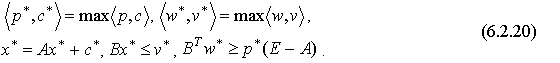
Благодаря линейности задач (6.2.18) и (6.2.19), такое равновесие существует.
В качестве упражнения читателю предлагается доказать существование равновесия (6.2.20). Указания: либо показать выполнение условий теоремы Эрроу-Дебре из §5.4; либо доказать напрямую, применяя схему доказательства теоремы Эрроу-Дебре, т.е. подведя к теореме Какутани о неподвижной точке для полунепрерывного сверху отображения множества нормированных цен
