Publisher: Springer Netherlands
Issue: Volume 7, Number 1 / December, 1955
Pages: 115-122
Приближенный метод расчета модели
межотраслевой баланса Леонтьева
Перевод с английского: Буток Е.П.
Введение
В модели межотраслевого баланса Леонтьева значения каждой из отраслей, связаных с характерным конечным спросом, как правило вычисляются с помощью обратной матрицы. Получение обратной матрицы достаточно трудоемкая работа. В данной статье рассматриваются простые способы вычисления приближенных значений модели межотраслевого баланса.
Методы аппроксимации
Пусть Yi — объем конечного продукта i-ой отрасли, Xi – общий объем продукции i-ой отрасли, связанный с конечным спросом Yi и aij — технологический коэффициент. Тогда система линейных уравнений Леонтьева записывается следующим образом:
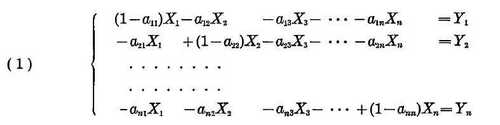
Эти линейные уравнения можно записать в виде:
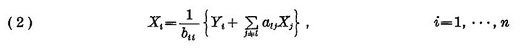
где bii=1-aii
Величина конечного спроса и объема продукции используются при расчете технологических коэффициентов aij, представленными Yi' и Xi', которые должны удовлетворять следующим уравнениям:
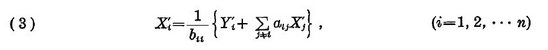
Подставим Xi(1)

который рассматривается в качестве приближения для Xi. Эти значения могут быть легко вычислены для известных Yi' и Xi' и исходного Yi.
Для получения лучшего результата оценим погрешность этого приближения. Из (3) и (4), получаем

Относительная погрешность приближения Xi
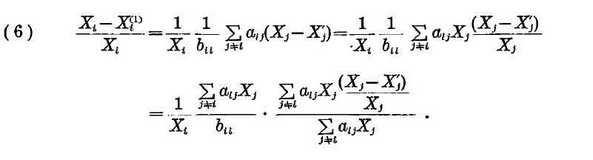
Так как

Из уравнений (6) и (7), имеем

Вычитая (3) из (2), получаем
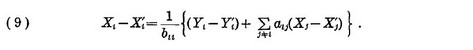
Из (9) и (8) следует, что
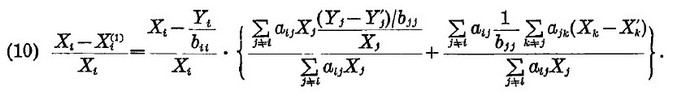
Так как Xi неизвестны, заменим Yi и Xi на Yi' и Xi', пренебрегаем вторым слагаемым в фигурных скобках в уравнении (10), то есть
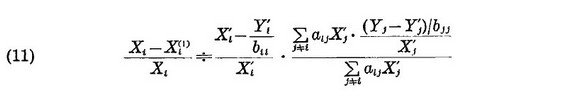
Где aijXj' затраты продукции i-ой отрасли на производство единицы стоимости j-ой отрасли и положительно коррелирует с Xi' при постоянном i. Заменим aijXj' на Xj', получим
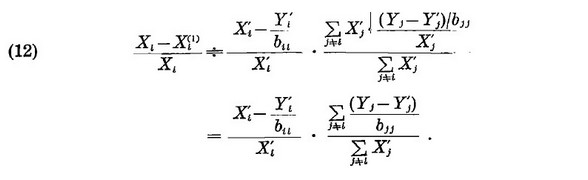
Используя эти значения, получаем лучшее приближение для Xi
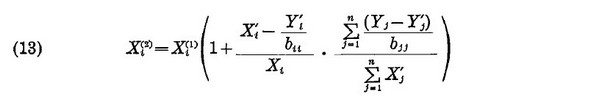
Для уравнения (13) в 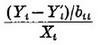 для больших Xi' используем
для больших Xi' используем 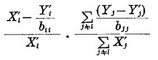 вместо
вместо 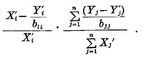
Из уравнений (2) и (3), имеем

Вычитая (15) из (14), и пренебрегая третий выражением, получим
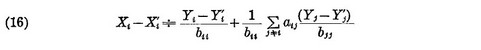
Второе выражении правой части (16) можно оценить аналогично тому, как и для (12), т. е.
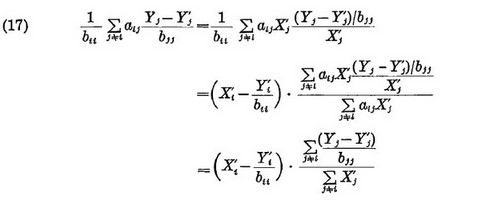
Тогда подставляя (17) в (16), мы получим приближение Xi(3) для Xi

Ошибки и замечания
Относительная погрешность для Xi(1), имеет почти такое же как и при Xi(1). В краткосрочный период аппроксимация удовлетворительна.
Для долгосрочного прогнозирования лучше воспользоваться приближением Xi(2) или Xi(3). Для двух аппроксимация вторые множители из Xi(1) в Xi(2) и из Xi' в Xi(3) одинаковы. Ошибки могут возникать при введении нами замены, хотя они достаточно малы, но должны быть приняты во внимание.
Для оценки этой ошибки, необходимо оценить разница между весом dij за счет разницы между  и
и
 для данного j
для данного j 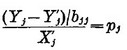 .
.
Видно, что 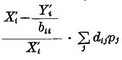 может дать приблизительную оценку ошибки.
может дать приблизительную оценку ошибки.
Далее оцениваем отброшенные компоненты по формуле:

В случае, если относительная погрешность является отрицательной, мы используем Xi(2). Когда она будет положительной, мы используем Xi(3).
Когда некоторые технологические коэффициенты изменяются в зависимости от полученных результатов, с учетом технологических изменений, используем значения конечного спроса, учитывая изменения технологических коэффициентов и результатов обследования. Значения конечного спроса могут быть легко вычислены.
Для получения лучшего результата используем метод последовательных приближений, при котором Xi(2) или Xi(3) берем для первого приближения. В этом случае стратификации Xi', используем Xi' для каждого коэффициента, где Xi' ошибочное. Таким образом, расчет производится гораздо проще.
Пример
Дана таблица технологических коэффициентов экономики Японии 1951 года, представленая Japan Economic Council Board. Значения Yi даны, Xi для 1952 прогнозируются.
Отрасли:
- Сельское, лесное и рыбное хозяйства
- Горная промышленность
- Строительство
- Обрабатывающая промышленность
- Оптовая и розничная торговля
- Транспорт и связь
- Коммунальные предприятия
- Сфера услуг
- и др.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| 1 | 0.128667 | 0.028314 | 0.017017 | 0.094223 | 0.002212 | 0.004733 | 0. | 0.28374 | 0.073596 |
| 2 | 0.000633 | 0.019320 | 0.027813 | 0.030733 | 0.000466 | 0.043543 | 0.312999 | 0.001587 | 0.007885 |
| 3 | 0.003796 | 0.005330 | 0.005124 | 0.004937 | 0.008963 | 0.017850 | 0.037058 | 0.010360 | 0. |
| 4 | 0.071494 | 0.124251 | 0.436780 | 0.413359 | 0.028635 | 0.151589 | 0.045610 | 0.089322 | 0.210514 |
| 5 | 0.031059 | 0.018654 | 0.043001 | 0.042147 | 0.006053 | 0.013387 | 0.015393 | 0.017547 | 0.030108 |
| 6 | 0.018866 | 0.048301 | 0.067521 | 0.038398 | 0.053661 | 0.037593 | 0.130559 | 0.046108 | 0.226284 |
| 7 | 0.000633 | 0.030646 | 0.000549 | 0.016016 | 0.010825 | 0.008555 | 0.012543 | 0.010267 | 0.014098 |
| 8 | 0.018751 | 0.026649 | 0.029643 | 0.018262 | 0.044695 | 0.077214 | 0.026226 | 0.090069 | 0.236798 |
| 9 | 0.008570 | 0.098268 | 0.068070 | 0.033553 | 0.022349 | 0.011765 | 0.062714 | 0.002240 | 0. |
| Xi' | Yi' | 1/bii | Yi'/bii | Xi'-Yi'/bii | (Xi'-Yi'/bii)/Xi' | Yi | |
| 1 | 17.386 | 9.228 | 1.147667 | 10.591 | 6.795 | 0.39 | 9.926 |
| 2 | 3.002 | 200 | 1.019701 | 204 | 2.798 | 0.93 | 259 |
| 3 | 5.465 | 4.704 | 1.005150 | 4.728 | 737 | 0.16 | 5.119 |
| 4 | 53.883 | 24.322 | 1.704620 | 41.460 | 12.423 | 0.23 | 24.351 |
| 5 | 8.591 | 4.997 | 1.006090 | 5.027 | 3.564 | 0.41 | 5.349 |
| 6 | 7.395 | 2.075 | 1.039061 | 2.502 | 4.893 | 0.66 | 2.408 |
| 7 | 1.754 | 432 | 1.012702 | 437 | 1.317 | 0.75 | 467 |
| 8 | 10.714 | 6.205 | 1.098984 | 6.819 | 3.895 | 0.36 | 7.955 |
| 9 | 4.185 | 1.147 | 1.0 | 1.147 | 3.038 | 0.72 | 657 |
| Всего | 112.375 | 702.915 | 39.460 |
| Yi-Yi' | (Yi-Yi')/bii | ∑(Yi-Yi')/bii))/∑Xj' | 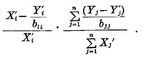 |
|
| 1 | 698 | 801 | 0.028 | 0.012 |
| 2 | 59 | 60 | 0.031 | 0.029 |
| 3 | 415 | 417 | 0.031 | 0.005 |
| 4 | 29 | 49 | 0.059 | 0.016 |
| 5 | 352 | 354 | 0.031 | 0.017 |
| 6 | 333 | 346 | 0.031 | 0.020 |
| 7 | 35 | 35 | 0.031 | 0.023 |
| 8 | 1750 | 1923 | 0.17 | 0.006 |
| 9 | - 490 | - 490 | 0.031 | 0.022 |
| Xi1 | Вероятность ошибки | Xi2 | Вероятность ошибки | (Xi'-Yi'/bii)*∑(Yi-Yi')/bii))/∑Xj' | |
| 1 | 18.187 | 0.8% | 18.405 | -0.4% | 190 |
| 2 | 3.062 | 2.7 | 3.151 | -0.1 | 88 |
| 3 | 5.882 | 0.8 | 5.911 | 0.3 | 23 |
| 4 | 53.932 | 1.5 | 54.795 | -0.1 | 733 |
| 5 | 8.945 | 1.3 | 9.061 | 0.03 | 110 |
| 6 | 7.741 | 1.7 | 7.896 | -0.3 | 152 |
| 7 | 1.789 | 2.1 | 1.830 | -0.1 | 41 |
| 8 | 12.637 | 0.2 | 2.713 | -0.4 | 66 |
| 9 | 3.695 | 2.9 | 3.776 | 0.8 | 94 |
| Xi3 | Вероятность ошибки | Xi для обратной матрицы | |
| 1 | 18.377 | -0.3% | 18.328 |
| 2 | 3.150 | -0.1 | 3.148 |
| 3 | 5.905 | 0.4 | 5.927 |
| 4 | 54.665 | 0.1 | 54.734 |
| 5 | 9.055 | 0.1 | 9.064 |
| 6 | 7.893 | -0.3 | 7.873 |
| 7 | 1.830 | -0.1 | 1.828 |
| 8 | 12.703 | -0.3 | 12.660 |
| 9 | 3.789 | 0.4 | 3.805 |
Publisher: Springer Netherlands
Issue: Volume 7, Number 1 / December, 1955
Pages: 115-122