Аннотация

Чудовская А.К. Выбор алгоритма выделения контура для реализации возможности распараллеливания о технологии CUDA. В данной статье рассматривается задача ускорения выделения контуров на изображениях путем распараллеливания алгоритма выделения по технологии CUDA, приводится обоснование выбора алгоритма для распараллеливания.

Общая постановка проблемы. По мере усиления автоматизации всех сфер человеческой деятельности задача машинного распознавания образов стала очень актуальной. Важнейшим этапом распознавания является выделение контуров распознаваемого объекта. Основными потребителями алгоритмов выделения контуров являются системы реального времени. Наиболее популярными представителями таких систем являются системы автоматического контроля качества производимой продукции, а так же системы слежения за соблюдением правил дорожного движения. Такие системы должны точно, а главное, быстро выделять контуры объектов на изображении, а затем классифицировать их и анализировать, либо сравнивать с шаблоном.

Постановка задач исследования. Для достижения необходимого быстродействия предлагается использовать программно-аппаратную платформу CUDA. Важным этапом в реализации системы является выбор алгоритма, который будет программироваться. Алгоритм должен выбираться таким образом, чтобы максимально эффективно использовать сильные стороны платформы.

Решение задач и результаты исследований. Технология CUDAпредставляет собой средства для выполнения произвольных расчетов на видеочипах производства NVidia. При этом архитектура графических чипов представляет собой множество независимых скалярных процессоров. Таким образом, главным преимуществом подобного решения является реальная параллельность вычислений, выполняемых на этих процессорах (в отличие от виртуальной параллельности, присущей центральному процессору).

Наиболее логичным выбором алгоритма выделения контура является нейросетевой алгоритм, так как нейроны в одном слое нейросети работают независимо друг от друга и являются идеальными кандидатами для вынесения на независимые скалярные процессоры.

Для реализации процедуры выделения кон­тура с помощью нейронной сети была принята следующая модель. На вход нейронной сети подается изображение окна наблюдения разме­ром m Х n. Это изображение удовлетворяет следующим требованиям:

1. Изображение всегда содержит элемент контура, то есть в любом представленном изображении содержится граница перепада яркостей объекта и фона.
2. На изображении только один контур, то есть не предусматривается работа алгоритма с множественными   контурами.
3. На изображении может присутствовать аддитивный гауссов шум, который пре­пятствует правильной работе алгоритма.

На выходе необходимо получить основные параметры прямой, аппроксимирующей грани­цу перепада яркости: u  — интенсивность фона, u + h — интенсивность объекта, d — расстояния от центра окна до прямой,   - угол наклона прямой. Данные параметры пока­заны на рис. 1.

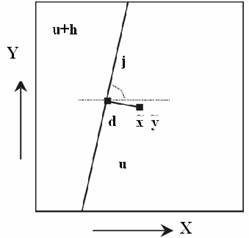
Рисунок 1 – Граница объект/фон в элементарном окне

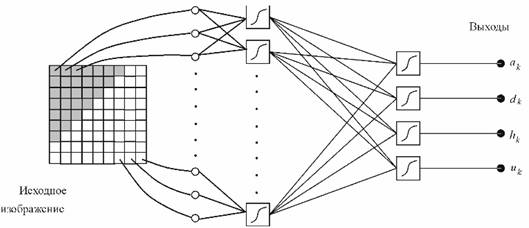
Для реализации этой модели была выбрана нейронная сеть типа многослой­ный персептрон, так как задача носит явно статис­тический характер. Сеть содержит два слоя. В первом слое 10 нейронов, во втором 4. Все искусственные нейроны используют логистическую функцию активации. Архитек­тура сети изображена на рис. 2.

Рисунок 2 – Архитектура нейросети

Следует обратить особое внимание на первое требование к окну изображения. Так как окна, подаваемые на нейросеть, должны обязательно содержать часть границы, и при том только одну (требование 2), то необходимо каким-либо образом эти окна найти. Одним из вариантов решения этой задачи является нахождение предварительного контура более быстрым и грубым методом. Затем найденное приближение контура разбивается на участки, которые уточняются на нейросети. Кроме того, отдельной задачей является сбор разрозненных участков контуров в один непрерывный контур. Решить эту задачу можно, к примеру, находя среднюю точку между двумя крайними точками аппроксимирующей прямой у двух соседних окон.

В качестве алгоритма предварительного определения контуров выбрана комбинация из нескольких этапов алгоритма Canny, а именно:

Шаг 1. Первым шагом является фильтрация шума в исходном изображении. Фильтр Гаусса можно вычислить с помощью простой маски. После того как подходящая маска была рассчитана, сглаживание Гаусса может быть выполнено с помощью стандартных методов свертки. Маски свертки, как правило, гораздо меньше, чем само изображение. В результате, маска двигается над изображением, манипулируя квадратом пикселей за один раз. Чем больше ширина маски Гаусса, тем меньше чувствительность детектора к шуму. Локализация ошибки в обнаружении краев так же немного увеличивается с увеличением ширины Гауссиана.

Шаг 2. Нахождение края силы путем взятия градиента изображения. Оператор Собеля выполняет 2-D пространственное измерение градиента в изображении. Тогда приближенные градиенты абсолютных величин (края сил) в каждой точке может быть найдено.  Оператор Собеля использует пару 3x3 масок свертки: оценки градиента в направлении х (столбцы) и оценки градиента в Y-направлении (строк). 

Величина, или край силы, градиента затем аппроксимируется по формуле: |G| = |Gx| + |Gy|

Шаг 3. Гистерезис используется в качестве средства устранения полос. Полоса – это разбиение контура края, вызванное оператором выходного колебания выше и ниже порогового уровня. Если единственный порог, T1 применяется к изображению и край имеет среднюю силу, равную T1, то из-за шума, будут случаи, когда край опускается ниже порогового уровня. В равной степени он будет также распространяться выше порога принятия края, похожего на  пунктирную линию. Чтобы избежать этого, гистерезис использует 2 порога, высокий и низкий. Любой пиксель в изображении, который имеет значение большее, чем T1 предположительно является краевым пикселем, и немедленно обозначается как таковой. Затем, любые пиксели, которые соединяются с этим краевым пикселем, и которые имеют значение, большее, чем T2, также выбираются как краевые пиксели. Для начала движения вдоль края необходим градиент T2, а для окончания – градиент ниже T1.

Этот алгоритм также может быть распараллелен для расчета на программно-аппаратном комплексе CUDA путем разбиения изображения на участки и расчет этих участков на разных процессорах.

В итоге все изображение разбивается на окна размером m X n, пригодные для обработки нейросетью, но обработке подвергаются только те из них, которые содержат ровно один участок контура.

Выводы. Существующие последовательные алгоритмы выделения контуров на изображениях не обладают достаточным быстродействием для применения в системах реального времени. В данной статье рассмотрен возможный способ улучшения алгоритма и оптимизация для распараллеливание его по технологии CUDA. В дальнейшем планируется программная реализация алгоритма и сравнение с уже существующими для определения эффективности предложенного улучшения.

Список литературы

1. А.И. Перов, Г.Г. Соколов. «Алгоритм последовательного выделения контура объекта на двумерных цифровых изображениях»– Радиотехника, №7, 1998

2. Bill Green. «Canny Edge Detection Tutorial» – http://www.pages.drexel.edu/~weg22/can_tut.html

3. А. А. Сирота, А. И. Соломатин. «Статистические алгоритмы обнаружения границ объектов на изображениях» – Вестник ВГУ, № 1, 2008