В последнее время стало ясно, что современные автоматические алгоритмы не способны решать произвольные задачи сегментации с гарантированным результатом. Более того, по всей видимости, в ближайшее время такие алгоритмы не появятся. Поэтому всё большее и большее внимание стало уделяться интерактивной сегментации изображений.
Настоящий прорыв в данной области произошёл в 2000 г. - с изобретением Юрием Бойковым и Мари-Пьер Джолли алгоритма GraphCut. Этот алгоритм де-факто стал эталонным. Большая часть новых алгоритмов интерактивной сегментации изображений являются развитием GraphCut-а. Остальные алгоритмы, сравниваются в первую очередь с ним. Разрезы графов, на которые опирается GraphCut, стали активно использоваться и в других областях компьютерного зрения: сегментации видео, ститчинге, стерео-реконструкции.
Интерактивная сегментация изображений активно используется для редактирования изображений, анализа медицинских данных, а также является составной частью многих алгоритмов компьютерного зрения.
В интерактивной сегментации изображений обычно рассматривается задача разбиения только на 2 области - объект и фон (разбиение на большее число областей получается многократным разбиением на 2 области).
На вход алгоритм получает:
В процессе работы алгоритма пользователь может уточнять или дополнять входные данные.
На выходе алгоритм должен дать разбиение исходного изображения, удовлетворяющее наложенным пользователям ограничениям. Это разбиение должно удовлетворять неким априорным представлениям пользователя о разбиении изображенных объектов.
Как видно, сама постановка задачи не является четкой. Как оценить априорное представление пользователя о разбиении объектов? В автоматической сегментации, для построения меры качества разбиения, используются предположения о том, что <похожесть> цвета пикселей, текстуры внутри одного объекта должна быть максимальной, а между объектами - минимальной. Но в интерактивной сегментации пользователь может делать сколь угодно много <подсказок> алгоритму - добавлять новые ограничения, уточнять входную информацию до тех пор, пока не получит ожидаемого результата. Понятно, что в пределе, когда пользователь явно укажет про каждый пиксель, к какой области он должен принадлежать, он всегда получит идеальную сегментацию. Можно было бы оценивать качество сегментации при одних и тех же подсказках, но различные алгоритмы получают различную входную информацию от пользователя.
Также в интерактивной сегментации предполагается, что пользователь при помощи <подсказок> алгоритму - дополнительного ввода, должен иметь возможность отсегментировать объект даже в тех случаях, когда его часть и по цвету и по текстуре ближе фону, чем оставшейся части объекта. Это тоже затрудняет создание объективных метрик.
Поэтому естественно, что для сравнения алгоритмов интерактивной сегментации чаще всего используют субъективное сравнение: берется несколько изображений, и нескольким пользователям ставится одна из 2 задач:
Magic Wand (<волшебная палочка>) является, наверное, самым известным и, возможно, самым простым алгоритмом интерактивной сегментации изображений. Она встроена практически в каждый современный графический редактор.
Пользователь указывает пиксель объекта и задаёт порог. Алгоритм относит к объекту область, включающую заданный пиксель, и цвета всех пикселей которой отличаются от цвета заданного пикселя не больше, чем на данный порог. По указанию пользователя можно выделить только связную подобласть, включающую заданный пиксель.
Очевидно, что данный алгоритм работает только в случаях, когда цветовое распределение фона и объекта не пересекаются.
В реальности для сегментации сложных объектов пользователю приходится выбрать маленький порог, и по очереди указывать алгоритму множество пикселей объекта, добавляя при этом маленькие кусочки к текущей маске объекта.
Примеры работы алгоритма показаны на рис. 2.
|
|
|
|
(а) |
(б) |
|
|
|
|
(в) |
(г) |
|
Рис. 2 Пример сегментации с помощью Magic Wand. На пример (а),(б) - ушло 8 кликов мыши, на пример (в), (г) ушло более 20 кликов, причем некоторые части оленя остались неотсегментированными из-за пересечения цветовых распределений фона и объекта. Изображения взяты из базы Беркли [2]. |
|
Intelligent Scissors (<Умные ножницы>) трактуют всё изображение как граф, каждая вершина которого соответствует пикселю изображения. Вершины, соответствующие соседним пикселям (используется 8-связность) связываются ребрами. На ребрах данного графа определяется весовая функция. Т.к. алгоритм основан на нахождении в графе путей минимальной стоимости, то значение этой функции должно быть мало на ребрах, соответствующих потенциальной границе на изображении.
Конкретнее, данная функция выглядит следующим образом:
,
где 
- показывает локальные максимумы градиента,
- показывает силу градиента (чем он больше, тем 
меньше),
- стимулирует более гладкие границы,
, 
, 
- эвристически подобранные коэффициенты.
Пользователь
указывает пиксель на границе объекта ("seed point" - семя). После чего алгоритм вычисляет путь минимальной стоимости от
этой вершины-семени до всех других вершин графа. В упрощенном случае, когда в 
не входит 
, данный процесс
представлен на рис. 3. Нужно заметить, что веса диагональных связей берутся с
учетом евклидового расстояния между вершинами (т.е. умножаются на 
).
|
|
|
||
|
(а) |
(б) |
||
|
|
|
|
|
|
(в) |
(г) |
(д) |
|
|
Рис. 3. Пример вычисления путей минимальной стоимости. (а) - исходный граф с указанными весами вершин; вершина, обведенная в кружок соответствует указанному пользователем пикселю, (в), (г), (д) - процесс подсчета минимального пути, различные стадии, (б) - граф с вычисленными минимальными путями от каждой вершины до заданной. |
|||
После этого пользователь двигает по изображению курсором, и ему моментально указывается наилучший путь, соединяющий исходный пиксель и пиксель под курсором.
Пример работы алгоритма продемонстрирован на рис. 4.
В [4] для ускорения этого алгоритма изначально используется пересегментация, после чего однородные области трактуются как вершины графа (вместо отдельных пикселей).
Главное ограничение данного алгоритма заключается в том, что в сильно текстурированных областях существует множество альтернативных <минимальных> путей. А это в свою очередь приводит к многочисленным взаимодействиям с пользователем.
Intelligent Scissors реализован, например, в инструменте Magnetic Lasso в Adobe Photoshop.
|
|
|
Рис. 4 Пример работы алгоритма Intelligent Scissors. |
Вначале, данный алгоритм производит автоматическую иерархическую сегментацию изображения - рис. 5
|
|
|
|
|
(а) |
(б) |
(в) |
|
Рис. 5. Пример иерархической сегментации изображения |
||
Пользователь проводит кисточкой по объекту, добавляя к нему области, на которые пришелся мазок. При этом алгоритмом автоматически к объекту добавляются соседние области, наиболее близкие по цвету к данным.
Результаты работы алгоритма приведены на рис. 6.
|
|
|
|
(а) |
(б) |
|
|
|
|
(в) |
(г) |
|
Рис. 6. Пример работы алгоритма Intelligent Paint. (а), (в) - исходные изображения, (б), (г) - результат сегментации, пунктирной линией изображено движение курсора. |
|
Как было сказано во введении, данный алгоритм стал основой большинства современных наилучших алгоритмов интерактивной сегментации, так что остановимся на этом алгоритме поподробнее.
Данный алгоритм,
также как и Intelligent Scissors, трактует всё
изображение, как граф. Но в данном случае к вершинам, соответствующим пикселям
изображения, добавляются 2 терминальные вершины, называемые истоком и стоком.
Вершины, соответствующие соседним пикселям 
и 
, связываются ребрами с весом 
, где 
- цвета пикселей, 
- настраиваемый параметр, а 
- евклидовое расстояние между
пикселями.
Пользователь указывает несколько пикселей, принадлежащих объекту (т.н. семена объекта), и несколько пикселей фона (семена фона). Вершины графа, соответствующие семенам объекта и фона, связываются соответственно с истоком и стоком ребрами с бесконечно большим весом.
После этого, в полученном графе находится минимальный разрез (отсюда и название самого алгоритма), который делит граф на 2 части. Пиксели, попавшие в один подграф с истоком, считаются объектом, остальные пиксели признаются фоном. Бесконечный вес ребер между семенами обеспечивает выполнение заданных пользователем ограничений: семена объекта будут отнесены к объекту, семена фона - к фону. Рис. 7 хорошо иллюстрирует данный алгоритм. Чем больше отличаются цвета соседних пикселей, тем вес ребра между ними меньше, а значит больше вероятность того, что разрез графа пройдет между ними. Это стимулирует прохождение разреза графа по наиболее контрастной границе.
|
|
|
|
(а) |
(б) |
|
|
|
|
(в) |
(г) |
|
Рис. 7. Иллюстрация алгоритма GraphCut. (а) - исходное изображение, O,B - семена объекта и фона; (б) - финальная сегментация; (в) - построенный граф, T и S - сток и исток соответственно; (г) - найденный минимальный разрез; |
|
Для нахождения самого минимального разреза авторы GraphCut-а разработали новый алгоритм, основанный на алгоритме Форда-Фалкерсона [7] Они не сумели строго доказать его превосходство в скорости над другими существующими алгоритмами, но на произведенных ими опытах (а также как показали многие эксперименты, произведенные позже другими исследователями) на графах, типичных для задач компьютерного зрения, данный алгоритм является более быстрым.
Также необходимо отметить, что при дополнительном вводе со стороны пользователя (указании новых семян объекта и фона), полный пересчет максимального потока не требуется. Максимальный поток в таком случае ищется только для остаточного графа. Это уменьшает время реакции алгоритма на дополнительный пользовательский ввод (хотя для больших изображений время реакции всё равно остаётся довольно большим).
В качестве
улучшения данного алгоритма было предложено использовать цветовую статистику объекта
и фона, собранную на основе отмеченных пользователем семян объекта и фона [8].
При использовании статистики, все обычные вершины (не только семена)
связываются ребрами с терминальными вершинами. Ребра, связывающие
нетерминальные вершины с истоком, получают вес
, где 
- вероятность цвета 
в цветовом распределении фона, 
- настраиваемый
коэффициент. Т.е. чем характерней цвет данного пикселя для цветов фона, тем сила
его связи с истоком меньше. Аналогично
вес ребер, связывающих нетерминальные вершины со стоком - 
Веса рёбер показаны в таблице 1:
|
ребро |
Вес |
Для |
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
Таблица 1. Веса рёбер в графе. O,B -семена объекта и фона соответственно, P -множество всех нетерминальных вершин, S,T - исток и сток соответственно |
||
Пусть 
- бинарный вектор, компоненты которого 
показывают принадлежность
пикселя 
либо объекту, либо фону (
, если 
принадлежит объекту, 
иначе).
GraphCut находит глобальный минимум следующей
энергии: 
,
где 
, 
и 
Энергия данных (data energy) 
- описывает
региональные свойства сегментации, т.е. то, насколько цвета всех пикселей
хорошо между собой согласуются. 
можно рассматривать,
как индивидуальное пенальти за отнесение пикселя к фону или объекту.
Регуляризирующая энергия
(smoothing energy)
включает в себя
граничные свойства сегментации и описывает резкость границы.
Т.о. GraphCut является <смешанным> алгоритмом, он уменьшает и региональную энергию, и граничную одновременно (в то время, как Magic Wand является чисто региональным, а Intelligent Scissor - чисто граничным).
Пример работы алгоритма показан на рис. 8.
|
|
|
|
(а) |
(б) |
|
Рис. 8. Пример работы алгоритма GraphCut. (а) - исходное изображение; (б) - итоговая сегментация, мазки, помеченные буквой B обозначают семена фона, буквой O - семена объекат. |
|
Данный алгоритм является развитием GraphCut-а. Главной целью разработчиков GrabCut-а было уменьшение взаимодействия алгоритма с пользователем, а именно они хотели сделать достаточным задание ограничивающего прямоугольника вокруг объекта для получения изначального приближения. Для этого они ввели итеративную схему сегментации.
Исходя из цветового распределения внутри и снаружи ограничивающего прямоугольника, строится первая цветовая статистика объекта и фона. В качестве цветовой модели используется смесь гауссиан со статически заданным количеством компонент. Затем поочередно производится сегментация (GraphCut-ом, использующим цветовую статистику) и уточнение цветовой статистики. После каждого уточнения цветовой статистики, граф (в котором ищется минимальный разрез) перевзвешивается.
Если пользователь не удовлетворен получившейся сегментацией, он может, также как и в GraphCut-е, отметить некоторые пиксели, которые обязаны принадлежать объекту или фону. Типичный процесс сегментации с помощью GrabCut-а продемонстрирован на рис. 1.
Некоторые примеры работы GrabCut-а приведены на рис. 9-10.
|
|
|
|
(а) |
(б) |
|
|
|
|
(в) |
(г) |
|
Рис. 9. Простые примеры сегментации GrabCut-ом. Цвета объекта и фона заметно различаются, поэтому алгоритму достаточно одного ограничивающего прямоугольника вокруг объекта. |
|
|
|
|
|
|
(а) |
(б) |
(в) |
|
|
|
|
|
(г) |
(д) |
(е) |
|
Рис.10. Сложные примеры сегментации GrabCut-ом. Цветовые распределения объекта и фона пересекаются, из-за чего алгоритму требуется дополнительные указания со стороны пользователя. (а), (г) - исходные изображения с указанными пользователем ограничивающими прямоугольниками; (б), (д) - дополнительный пользовательский ввод; (в), (е) - финальная сегментация. |
||
GrabCut запатентован компанией Microsoft и реализован в одной из рабочих версий графического редактора Microsoft Expression [10] (версия V4.0d). Данная реализация получила множество восторженных отзывов со стороны пользователей, однако по непонятным причинам была исключена из последующих версий редактора.
Ещё одно развитие GraphCut-а. Процесс сегментации с помощью Lazy Snapping изображен на рис. 11.
|
|
|
|
(а) |
(б) |
|
|
|
|
(в) |
(г) |
|
Рис. 11. Процесс сегментации Laze Snapping. (а) - исходное изображение; (б) - первый шаг алгоритма: пользователь указывает всего 3 линии (2 внутри объекта, 1 снаружи), все линии рисуются далеко от границы; (в) - второй шаг алгоритма: полигональное редактирование границы объекта; (г) - композиция вырезанного изображения и ещё одной картины Ван Гога. |
|
Весь алгоритм состоит из 2 шагов.
На первом шаге выполняется пересегментация изображения (авторы использовали watershed алгоритм [12]). После чего выполняется обычный GraphCut, только в качестве вершин разрезаемого графа служат не отдельные пиксели изображения, а однородные области, получившиеся в результате пересегментации. Это обеспечивает значительный прирост скорости по сравнению с GraphCut-ом. Авторами особо подчеркивается сильное уменьшение времени реакции на дополнительный ввод пользователя.
На втором шаге, получившаяся граница объекта преобразуется в полигон. Для редактирования границы объекта пользователь может
Прежний полигон, соединяющий точки A и B заменяется новым, который находится тоже с помощью GraphCut-а: пиксели на границе мазка, лежащие внутри объекта, становятся семенами объекта, а пиксели на границе мазка, лежащие внутри фона - семенами фона. После чего уточненная граница вычисляется с помощью нахождения минимального разреза в этом графе - рис. 12 (б).Весовая функция рёбер немножко изменена по сравнению с исходной для стимулирования прохождения разреза вдоль середины мазка (для тех случаев, когда в области нет видимых границ).
|
|
|
|
(а) |
(б) |
|
Рис. 12. Пример редактирования границы с помощью Overriding Brush. |
|
Примеры работы Lazy Snapping изображены на рис. 13.
|
|
|
|
(а) |
(б) |
|
|
|
|
(в) |
(г) |
|
Рис. 13. Примеры сегментации с помощью Lazy Snapping. Показан только первый шаг алгоритма и итоговая сегментация. |
|
Данное развитие GraphCut-а модифицирует стадию обработки изначальной сегментации
На рис. 14. а), б) показано типичное поведение GraphCut-а. Алгоритм ошибочно определил часть земли в верхнем правом углу изображения, как объект. Пользователь помечает часть пикселей в этой области, как принадлежащие фону, но в результате этого, часть спины собаки тоже переходит к фону.
|
|
|
|
(а) |
(б) |
|
Рис. 14. Пример редактирования изначальной сегментации в GraphCut-е. Кроме участка земли в верхнем правом углу, к фону перешел участок спины собаки. |
|
Progressive Cut пытается понять намерение пользователя, лежащее под тем или иным дополнительным вводом.
Во-первых, анализируется, какой тип изменения ожидает пользователь. Например, если он отмечает дополнительные семена объекта в области, отнесенной алгоритмом к фону, то он не ожидает, что текущая область объекта от этого уменьшится (что может случиться в GraphCut-е, использующем статистику). А значит вершины графа, соответствующие пикселям внутри объекта можно выкинуть из графа, т.к. они не изменят своей принадлежности - см. рис. 15. Вершины же на границе объекта связываются с терминальной вершиной объекта ребрами бесконечного веса, что гарантирует их принадлежность объекту.
|
|
|
|
(а) |
(б) |
|
Рис. 15. Построение уменьшенного графа на стадии редактирования изначальной сегментации. |
|
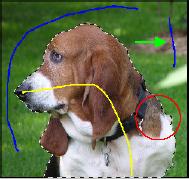
Во-вторых, пользователь обычно ожидает изменения в относительно небольшой области вокруг только что помеченных пикселей. Это записывается в виде дополнительной энергии, энергии <намерения> (intention energy), которая обратно пропорциональна расстоянию от данного пикселя до новых семян - см. рис. 16
|
|
|
|
(а) |
(б) |
|
Рис. 16. Пример редактирования изначальной сегментации в Progressive Cut. (а) - визуализация энергии <намерения>, большая яркость соответствует большей величине энергии; (б) - результат редактирования |
|
Несколько сравнений Progressive Cut и GraphCut-а приведены на рис. 17.
|
|
|
|
|
(а) |
(б) |
(в) |
|
|
|
|
|
(г) |
(д) |
(е) |
|
Рис. 17. Сравнение редактирования изначальной сегментации с помощью GraphCut и Progressive Cut. (а), (г) - изначальная сегментация, (б),(д) - результат редактирования с помощью GraphCut, (в), (е) - результат редактирования с помощью Progressive Cut. |
||
Данный алгоритм способен сразу сегментировать изображение на K>=2 области. Получая на вход отмеченные метками 1..K пиксели, алгоритм аналитически вычисляет вероятность того, что случайный странник (random walker), начинающий свой путь в каждом конкретном пикселе, первым достигнет один из помеченных пикселей. Итоговая сегментация получается присвоением каждому пикселю метки, вероятность прийти к которой из данного пикселя - максимальна.
Математически, данная задача сводится к решению больших систем линейных уравнений.
Первые реализации данного алгоритма были слишком медленными, чтобы называться интерактивными. Но с переложением алгоритма на GPU [15], его скорость возросла на порядок. Однако максимальное разрешение изображения при этом ограничено 1 мегапикселем.
Дальнейшее развитие исходного алгоритма также включало использование непараметрической вероятностной модели распределения цветов в разных областях [16].
Примеры работы алгоритма изображены на рис. 18.
|
|
|
|
(а) |
(б) |
|
Рис. 18. Примеры сегментации с помощью алгоритма Random Walker.Серой линией обозначены семена объекта и фона, отмеченные пользователем. Границы результирующих сегментов отмечены черной линией. |
|
Этот
алгоритм основывается на клеточных автоматах. Каждый пиксель изображения
представляется клеткой автомата. Состояние каждой клетки описывается
вектором 
, где 
- метка ('объект', 'фон',
'неизвестно'), 
- сила клетки, 
- вектор признаков
клетки (RGB цвет соответствующего пикселя). Клетки, соответствующие пикселям,
помеченным пользователем как принадлежащие объекту или фону, получают
соответствующие метки и силу 
= 1, все остальные
клетки имеют силу 
= 0, и метку 'неизвестно'.
Вводится монотонно
убывающая функция 
, изменяющаяся в диапазоне [0,1], которая описывает близость
цветов двух пикселей (x обычно является нормой разницы цветов пикселей).
Базовый вариант развития клеточного автомата можно описать следующим образом:
на каждой итерации каждую клетку 
'атакуют' все её
соседи 
(клетки,
соответствующие соседним пикселям): если 
, то происходит 'захват' данной клетки - её метка меняется на
метку 'захватчика', а её сила становится равной 
.
Процесс эволюции клеточного автомата проиллюстрирован на рис. 19.
Данный алгоритм очевидным образом обобщается на случай более 2 сегментов.
|
|
||||
|
(а) |
(б) |
||||
|
|
|
|
|
|
|
|
(в) |
(г) |
(д) |
(е) |
(ж) |
|
|
Рис. 19. Процесс эволюции клеточного автомата. (а) - исходное изображение с отмеченными пользователем семенами объекта (красные) и фона (синие); (б) - финальная сегментация; (в) - (ж) - развитие клеточного автомата: белым отмечены клетки объекта, черным - фона, серым - ещё незахваченные клетки. |
|||||
Главным достоинством алгоритма является его полная интерактивность. Т.к. любой дополнительный ввод приводит только к локальным изменениям, то время реакции алгоритма близко к нулю, в то время, как время реакции GraphCut-а для больших изображений может быть существенным.
В качестве развития данного алгоритма были предложены иерархическая версия, значительно ускоряющая базовый алгоритм, а также версия, налагающая на границы итоговых сегментов дополнительные ограничения на гладкость.
Т.к. алгоритм основан на клеточных автоматах, он легко реализуется на GPU [18].
Данный алгоритм реализован в виде одноименного плагина к Adobe Photoshop-у [19].
Примеры работы алгоритма изображены на рис. 20.
|
|
|
|
(а) |
(б) |
|
|
|
|
(в) |
(г) |
|
Рис. 20. Пример сегментации с помощью алгоритма GrowCut. (а), (в) - исходные изображения с отмеченными пользователем семенами разных сегментов; (б), (г) - результат сегментации на 2 и 3 области соответственно. |
|
Как было сказано в разделе <Оценка качества работы алгоритмов> сравнение различных алгоритмов интерактивной сегментации в основном субъективное. Причем, по нашей информации, обширных тестирований, включающих все, или хотя бы большинство, из описанных здесь алгоритмов, никто не проводил. Однако, некоторые вещи сказать можно.
Magic Wand является самым примитивным инструментом сегментации. Почти любая задача сегментации требует большого взаимодействия с пользователем. Однако, благодаря своей простоте реализации, получил наибольшее распространение.
Intelligent Scissors также требует достаточно большого количества действий со стороны пользователя (хотя и меньше, чем в Magic Wand). Причем пользователь должен ставить опорные точки в самой близи от границы объекта, что достаточно утомительно. К плюсам стоит отнести высокую скорость алгоритма.
Intelligent Paint, судя по анализу, проведенному авторами этого алгоритма, требует меньше времени для сегментации, чем 2 предыдущих алгоритма. Однако, некоторые опасения вызывает тот факт, что, несмотря, на то, что алгоритм придуман относительно давно, по нашим сведениям, он не реализован в коммерческих программах.
GraphCut значительно упрощает действия пользователя по сравнению с предыдущими алгоритмами. Главным недостатком является значительное время реакции на дополнительный ввод для больших изображений (в несколько мегапикселей). Также стоит отметить, что алгоритм требует достаточно много оперативной памяти. Запатентован.
GrabCut обладает самым удобным интерфейсом среди всех рассматриваемых алгоритмов, т.к. позволяет получить первое приближение по одному ограничивающему прямоугольнику. Однако в случаях, когда цветовые распределения фона и объекта сильно перекрываются, первое приближение часто выдаёт неправильный результат, и изображение приходится сегментировать также, как и в обычном GraphCut-е. Сложнее остальных алгоритмов для реализации [20]. Запатентован.
Lazy Snapping, сохраняя достоинства GraphCut-а, значительно уменьшает время реакции на дополнительный ввод. GrabCut и Lazy Snapping на наш взгляд являются наилучшими алгоритмами интерактивной сегментации изображений.
Progressive Cut упрощает процесс редактирования сегментации. Однако изменение исходного графа может увеличить время реакции алгоритма (авторы не предоставляли информации о скорости алгоритма)
Random Walker, по нашему мнению, проигрывает GraphCut-у. Время реакции больше, чем у последнего. Также требует много оперативной памяти.
GrowCut, несмотря на простоту реализации, является достаточно хорошим алгоритмом сегментации. Главным достоинством является очень маленькое время реакции на дополнительный ввод, и вследствие этого, высокая интерактивность. К недостаткам следует отнести некоторую рваность границ. Достаточно требователен к оперативной памяти.
