Iterative methods for sparce linear systems[abstract]:Storage Schemes, Basic Sparse Matrix Operations
Автор:Yousef Saad
Источник:http://www-users.cs.umn.edu/~saad/PS/iter1.pdf
STORAGE SCHEMES
In order to take advantage of the large number of zero elements, special schemes are required to store sparse matrices. The main goal is to represent only the nonzero elements, and to be able to perform the common matrix operations. In the following, Nz denotes the total number of nonzero elements. Only the most popular schemes are covered here, but additional details can be found in books such as Duff, Erisman, and Reid.
The simplest storage scheme for sparse matrices is the so-called coordinate format. The data structure consists of three arrays: (1) a real array containing all the real (or complex) values of the nonzero elements of A in any order; (2) an integer array containing their row indices; and (3) a second integer array containing their column indices. All three arrays are of length Nz, the number of nonzero elements.
Example 1 The matrix
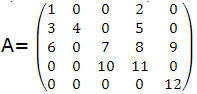
will be represented (for example) by:
| AA | 12 | 9 | 7 | 5 | 1 | 2 | 11 | 3 | 6 | 4 | 8 | 10 |
| JR | 5 | 3 | 3 | 2 | 1 | 1 | 4 | 2 | 3 | 2 | 3 | 4 |
| JC | 5 | 5 | 3 | 4 | 1 | 4 | 4 | 1 | 1 | 2 | 4 | 3 |
In the above example, the elements are listed in an arbitrary order. In fact, they are usually listed by row or columns. If the elements were listed by row, the array JC which contains redundant information might be replaced by an array which points to the begin¬ning of each row instead. This would involve nonnegligible savings in storage. The new data structure has three arrays with the following functions:
- A real array AA contains the real values Ojj stored row by row, from row 1 to n. The length of AA is Nz.
- An integer array JA contains the column indices of the elements ay as stored in the array A. The length of JA is Nz.
- An integer array IA contains the pointers to the beginning of each row in the arrays AA and JA. Thus, the content of IA(i) is the position in arrays AA and JA where the i-th row starts. The length of IA is n + 1 with IA(n +1) containing the number IA(1) + Nz, i.e., the address in A and JA of the beginning of a fictitious row number n + 1.
Thus, the above matrix may be stored as follows:
| AA | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| JА | 1 | 4 | 1 | 2 | 4 | 1 | 3 | 4 | 5 | 3 | 4 | 5 |
| IA | 1 | 3 | 6 | 10 | 12 | 13 |
This format is probably the most popular for storing general sparse matrices. It is called the Compressed Sparse Row (CSR) format. This scheme is preferred over the coor¬dinate scheme because it is often more useful for performing typical computations. On the other hand, the coordinate scheme is advantageous for its simplicity and its flexibility. It is often used as an "entry" format in sparse matrix software packages.
There are a number of variations for the Compressed Sparse Row format. The most obvious variation is storing the columns instead of the rows. The corresponding scheme is known as the Compressed Sparse Column (CSC) scheme.
Another common variation exploits the fact that the diagonal elements of many matrices are all usually nonzero and/or that they are accessed more often than the rest of the elements. As a result, they can be stored separately. The Modified Sparse Row (MSR) format has only two arrays: a real array AA and an integer array JA. The first n positions in AA contain the diagonal elements of the matrix in order. The position n+1 of the array AA is not used, but may sometimes be used to carry other information concerning the matrix. Starting at position n + 2, the nonzero elements of AA, excluding its diagonal elements, are stored by row. For each element AA(k), the integer JA(k) represents its column index on the matrix. The n + 1 first positions of JA contain the pointer to the beginning of each row in AA and JA. Thus, for the above example, the two arrays will be as follows:
| AA | 1 | 4 | 7 | 11 | 12 | * | 2 | 3 | 5 | 6 | 8 | 9 | 10 |
| JА | 7 | 8 | 10 | 13 | 14 | 14 | 4 | 1 | 4 | 1 | 4 | 5 | 3 |
The star denotes an unused location. Notice that JA(n) = JA(n + 1) = 14, indicating that the last row is a zero row, once the diagonal element has been removed.
Diagonally structured matrices are matrices whose nonzero elements are located along a small number of diagonals. These diagonals can be stored in a rectangular ar¬ray DIAG(1 :n, 1 :Nd), where Md is the number of diagonals. The offsets of each of the diagonals with respect to the main diagonal must be known. These will be stored in an array I0FF(1:Nd). Thus, the element ai,i+ioff(j) of the original matrix is located in position (i,j) of the array DIAG, i.e.,
The order in which the diagonals are stored in the columns of DIAG is generally unimportant, though if several more operations are performed with the main diagonal, storing it in the first column may be slightly advantageous. Note also that all the diagonals except the main diagonal have fewer than n elements, so there are positions in DIAG that will not be used.
Example 2 For example, the following matrix which has three diagonals
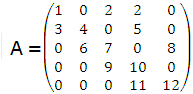
DIAG =
| * | 1 | 2 |
| 3 | 4 | 5 |
| 6 | 7 | 8 |
| 9 | 10 | * |
| 11 | 12 | * |
| -1 | 0 | 2 |
A more general scheme which is popular on vector machines is the so-called Ellpack-Itpack format. The assumption in this scheme is that there are at most Nd nonzero elements per row, where Nd is small. Then two rectangular arrays of dimension n x Nd each are required (one real and one integer). The first, C0EF, is similar to DIAG and contains the nonzero elements of A. The nonzero elements of each row of the matrix can be stored in a row of the array C0EF (1: n, 1: Nd), completing the row by zeros as necessary. Together with CDEF, an integer array JC0EF (1: n, 1: Nd) must be stored which contains the column positions of each entry in C0EF.
Example 3 Thus, for the matrix of the previous example, the Ellpack-Itpack storage scheme is
COEF =| 1 | 2 | 0 |
| 3 | 4 | 5 |
| 6 | 7 | 8 |
| 9 | 10 | 0 |
| 11 | 12 | 0 |
| 1 | 3 | 1 |
| 1 | 2 | 4 |
| 2 | 3 | 5 |
| 3 | 4 | 4 |
| 4 | 5 | 5 |
BASIC SPARSE MATRIX OPERATIONS
The matrix-by-vector product is an important operation which is required in most of the iterative solution algorithms for solving sparse linear systems. This section shows how these can be implemented for a small subset of the storage schemes considered earlier.
The following Fortran 90 segment shows the main loop of the matrix-by-vector operation for matrices stored in the Compressed Sparse Row stored format.
DO 1=1, N Kl = IA(I) K2 = IA(I+1)-1 Y(I) = D0TPR0DUCT(A(K1:K2),X(JA(K1:K2))) ENDDO
Notice that each iteration of the loop computes a different component of the resulting vector. This is advantageous because each of these components can be computed independently. If the matrix is stored by columns, then the following code could be used instead:
DO J=l, N Kl = IA(J) K2 = IA(J+1)-1 Y(JA(K1:K2)) = Y(JA(K1:K2))+X(J)*A(Kl:K2) ENDDO
In each iteration of the loop, a multiple of the j-th column is added to the result, which is assumed to have been initially set to zero. Notice now that the outer loop is no longer parallelizable. An alternative to improve parallelization is to try to split the vector operation in each inner loop. The inner loop has few operations, in general, so this is unlikely to be a sound approach. This comparison demonstrates that data structures may have to change to improve performance when dealing with high performance computers. Now consider the matrix-by-vector product in diagonal storage.
DO J=l, N JOFF = IOFF(J) DO 1=1, N Y(I) = Y(I) +DIAG(I,J)*X(J0FF+I) ENDDO ENDDO
Here, each of the diagonals is multiplied by the vector x and the result added to the vector y. It is again assumed that the vector y has been filled with zeros at the start of the loop. From the point of view of parallelization and/or vectorization, the above code is probably the better to use. On the other hand, it is not general enough.
Solving a lower or upper triangular system is another important “kernel” in sparse matrix computations. The following segment of code shows a simple routine for solving a unit lower triangular system Lx = y for the CSR storage format.
X(l) = Y(l) DO I = 2, N Kl = IAL(I) K2 = IAL(I+1)-1 X(I)=Y(I)-D0TPRDDUCT(AL(K1:K2),X(JAL(K1:K2))) ENDDO
At each step, the inner product of the current solution x with the i-th row is computed and subtracted from y(i). This gives the value of x(i). The dotproduct function computes the dot product of two arbitrary vectors u(kl:k2) and v(kl:k2). The vector AL(K1:K2) is the i-th row of the matrix L in sparse format and X(JAL(K1:K2)) is the vector of the components of X gathered into a short vector which is consistent with the column indices of the elements in the row AL (K1: K2).