Разработка эффективного алгоритма решения СЛАУ на разреженных матрицах общего вида

Авторы: Дяченко Т.Ф., Михайлова Т.В.
Источник: Тезизы доклада на IV международной научно-практической конференции молодых ученых, аспирантов,студентов «Современная информационная Украина: Информатика, Экономика, Философия», 13-14 мая 2010г., Государственный Университет информатики и искусственного интеллекта, Донецк

Создание и использование современных суперкомпьютерных систем стало в наше время одним из основных направлений в ведущих странах мира. Одной из основных проблем, возникающих при проектировании и эксплуатации параллельных и распределенных вычислительных систем (ВС) является выработка рекомендаций рационального использования ресурсов вычислительной среды. Одним из эффективных способов решения этой проблемы может быть использование результатов непрерывных [1] или дискретных аналитических моделей.

В данной работе рассматриваются разреженные матрицы общего вида, получаемые при построении Марковских моделей вычислительных систем. Порядок возникающих матриц — от десятков и сотен тысяч до десятков миллионов. Это вызвано желанием оперировать более точными дискретными моделями, позволяющими получать приближенные решения, более близкие к решениям исходных задач, лучше учитывать локальные особенности рассматриваемого процесса.

Рассмотрим, например, матрицы какого вида получаются при построении дискретной Марковской модели вычислительного кластера.

Параметрами данной модели являются:

N — количество узлов в моделируемой системе (устройств или их блоков)

M — количество заявок в системе.

Число состояний системы равно числу размещений j задач по N узлам и определяется по формуле:

,

.

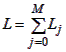Общее количество ненулевых элементов матрицы переходных вероятностей вычисляется как:

В таблице приведены результаты расчетов доли ненулевых элементов в матрице переходных вероятностей для модели с тремя группами устройств N=3 [2].

Количество задач М
20	50	100	200
Размерность матрицы переходных вероятностей (количество состояний модели)
1771*1771	23426*23426	176851*176851	1373701*1373701
Количество ненулевых элементов
1257408	94113953	2746496028	83871314553
Доля ненулевых элементов в матрице переходных вероятностей
0.4009	0.1715	0.0878	0.0444

Размерность получаемых матриц зависит от количества задач в моделируемой системе.

Важной особенностью получаемых матриц является тот факт, что сумма элементов по каждой строке равна единице, независимо от их числа. Отсюда вытекает еще одна сложность обработки таких матриц: порядок элементов в матрице может сильно разниться — от 0,5 до 10^-17. То есть к подобным матрицам нельзя применить масштабирование без потерь точности.

Следующей особенностью получаемых матриц является то, что они общего вида, т.е. не могут просто быть преобразованы к одному из стандартных видов: симметричному, ленточному, блочно-диагональному с окаймлением и т.п., для которых уже разработаны эффективные параллельные алгоритмы [3]

Итак, к разрабатываемому алгоритму решения СЛАУ на таких разреженных матриц выдвигается ряд требований:

• схема хранения матрицы должна быть особой: хранятся только ненулевые элементы и информация об их расположении в исходной матрице;
• метод решения СЛАУ предотвращать потерю точности при вычислениях
• параллельный алгоритм должен быть эффективным и масштабируемым.

Список литературы

1. Varki Е. Response Time Analysis of Parallel Computer and Storage Systems // IEEE Transactions on Parallel and Distributed Systems, vol. 12, №11, nov.2001. — рр.1146-1161
   
   
2. Михайлова Т.В. Распараллеливание алгоритма построения дискретной Марковской модели // Интеллектуальные и многопроцессорные системы 2005. Материалы научно-технической конференции. Геленджик, 26 сентября-1 октября 2005г.— Таганрог—Донецк—Минск, 2005, т.1.—с. 215-217
   
   
3. Ильин В.П. Проблемы высокопроизводительных технологий решения больших разреженных СЛАУ // Вычислительные методы и программирование. 2009. Раздел 1. — с. 141-147