http://www.qi.tnw.tudelft.nl/Courses/FIP/noframes/fip-Segmenta.html

 

 

Segmentation

  1. Thresholding
  2. Edge finding

 

In the analysis of the objects in images it is essential that we can distinguish between the objects of interest and "the rest." This latter group is also referred to as the background. The techniques that are used to find the objects of interest are usually referred to as segmentation techniques - segmenting the foreground from background. In this section we will two of the most common techniques - thresholding and edge finding - and we will present techniques for improving the quality of the segmentation result. It is important to understand that:

  1. there is no universally applicable segmentation technique that will work for all images, and,
  2. no segmentation technique is perfect.

 

 

Thresholding

 

This technique is based upon a simple concept. A parameter called the brightness threshold is chosen and applied to the image a[m,n] as follows:

 

 

This version of the algorithm assumes that we are interested in light objects on a dark background. For dark objects on a light background we would use:

 

 

The output is the label "object" or "background" which, due to its dichotomous nature, can be represented as a Boolean variable "1" or "0". In principle, the test condition could be based upon some other property than simple brightness (for example, If (Redness{a[m,n]} >= red), but the concept is clear.

The central question in thresholding then becomes: how do we choose the threshold? While there is no universal procedure for threshold selection that is guaranteed to work on all images, there are a variety of alternatives.

 

1.                 Fixed threshold - One alternative is to use a threshold that is chosen independently of the image data. If it is known that one is dealing with very high-contrast images where the objects are very dark and the background is homogeneous (Section 10.1) and very light, then a constant threshold of 128 on a scale of 0 to 255 might be sufficiently accurate. By accuracy we mean that the number of falsely-classified pixels should be kept to a minimum.

 

 

2.                 Histogram-derived thresholds - In most cases the threshold is chosen from the brightness histogram of the region or image that we wish to segment. (See Sections 3.5.2 and 9.1.) An image and its associated brightness histogram are shown in Figure 51.

A variety of techniques have been devised to automatically choose a threshold starting from the gray-value histogram, {h[b] | b = 0, 1, ... , 2B-1}. Some of the most common ones are presented below. Many of these algorithms can benefit from a smoothing of the raw histogram data to remove small fluctuations but the smoothing algorithm must not shift the peak positions. This translates into a zero-phase smoothing algorithm given below where typical values for W are 3 or 5:

 

 

 

 

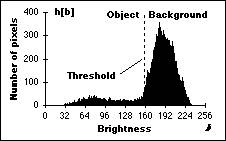
(a) Image to be thresholded (b) Brightness histogram of the image

 

Figure 51: Pixels below the threshold (a[m,n] < ) will be labeled as object pixels; those above the threshold will be labeled as background pixels.

 

* Isodata algorithm - This iterative technique for choosing a threshold was developed by Ridler and Calvard . The histogram is initially segmented into two parts using a starting threshold value such as 0 = 2B-1, half the maximum dynamic range. The sample mean (mf, 0) of the gray values associated with the foreground pixels and the sample mean (mb,0) of the gray values associated with the background pixels are computed. A new threshold value 1 is now computed as the average of these two sample means. The process is repeated, based upon the new threshold, until the threshold value does not change any more. In formula:

 

 

 

* Background-symmetry algorithm - This technique assumes a distinct and dominant peak for the background that is symmetric about its maximum. The technique can benefit from smoothing as described in eq. The maximum peak (maxp) is found by searching for the maximum value in the histogram. The algorithm then searches on the non-object pixel side of that maximum to find a p% point as in eq. (39).

In Figure 51b, where the object pixels are located to the left of the background peak at brightness 183, this means searching to the right of that peak to locate, as an example, the 95% value. At this brightness value, 5% of the pixels lie to the right (are above) that value. This occurs at brightness 216 in Figure 51b. Because of the assumed symmetry, we use as a threshold a displacement to the left of the maximum that is equal to the displacement to the right where the p% is found. For Figure 51b this means a threshold value given by 183 - (216 - 183) = 150. In formula:

This technique can be adapted easily to the case where we have light objects on a dark, dominant background. Further, it can be used if the object peak dominates and we have reason to assume that the brightness distribution around the object peak is symmetric. An additional variation on this symmetry theme is to use an estimate of the sample standard deviation (s in eq. (37)) based on one side of the dominant peak and then use a threshold based on  = maxp +/- 1.96s (at the 5% level) or  = maxp +/- 2.57s (at the 1% level). The choice of "+" or "-" depends on which direction from maxp is being defined as the object/background threshold. Should the distributions be approximately Gaussian around maxp, then the values 1.96 and 2.57 will, in fact, correspond to the 5% and 1 % level.

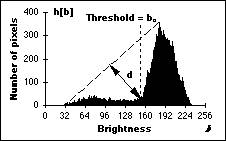
* Triangle algorithm - This technique due to Zack [36] is illustrated in Figure 52. A line is constructed between the maximum of the histogram at brightness bmax and the lowest value bmin = (p=0)% in the image. The distance d between the line and the histogram h[b] is computed for all values of b from b = bmin to b = bmax. The brightness value bo where the distance between h[bo] and the line is maximal is the threshold value, that is,  = bo. This technique is particularly effective when the object pixels produce a weak peak in the histogram.

 

 

Figure 52: The triangle algorithm is based on finding the value of b that gives the maximum distance d.

 

 

The three procedures described above give the values  = 139 for the Isodata algorithm,  = 150 for the background symmetry algorithm at the 5% level, and  = 152 for the triangle algorithm for the image in Figure 51a.

 

Thresholding does not have to be applied to entire images but can be used on a region by region basis. Chow and Kaneko developed a variation in which the M x N image is divided into non-overlapping regions. In each region a threshold is calculated and the resulting threshold values are put together (interpolated) to form a thresholding surface for the entire image. The regions should be of "reasonable" size so that there are a sufficient number of pixels in each region to make an estimate of the histogram and the threshold. The utility of this procedure-like so many others-depends on the application at hand.

 

 

Edge finding

 

 

Thresholding produces a segmentation that yields all the pixels that, in principle, belong to the object or objects of interest in an image. An alternative to this is to find those pixels that belong to the borders of the objects. Techniques that are directed to this goal are termed edge finding techniques. From our discussion in Section 9.6 on mathematical morphology, specifically eqs. , , and , we see that there is an intimate relationship between edges and regions.

 

 

1.                 Gradient-based procedure - The central challenge to edge finding techniques is to find procedures that produce closed contours around the objects of interest. For objects of particularly high SNR, this can be achieved by calculating the gradient and then using a suitable threshold. This is illustrated in Figure 53.

 

 

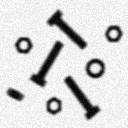
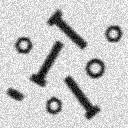
(a) SNR = 30 dB (b) SNR = 20 dB

 

Figure 53: Edge finding based on the Sobel gradient, eq. (110), combined with the Isodata thresholding algorithm

 

While the technique works well for the 30 dB image in Figure 53a, it fails to provide an accurate determination of those pixels associated with the object edges for the 20 dB image in Figure 53b. A variety of smoothing techniques as described in Section 9.4 and in eq. can be used to reduce the noise effects before the gradient operator is applied.

 

 

* Zero-crossing based procedure - A more modern view to handling the problem of edges in noisy images is to use the zero crossings generated in the Laplacian of an image (Section 9.5.2). The rationale starts from the model of an ideal edge, a step function, that has been blurred by an OTF such as Table 4 T.3 (out-of-focus), T.5 (diffraction-limited), or T.6 (general model) to produce the result shown in Figure 54.

 

 

 

Figure 54: Edge finding based on the zero crossing as determined by the second derivative, the Laplacian. The curves are not to scale.

 

 

The edge location is, according to the model, at that place in the image where the Laplacian changes sign, the zero crossing. As the Laplacian operation involves a second derivative, this means a potential enhancement of noise in the image at high spatial frequencies; see eq. (114). To prevent enhanced noise from dominating the search for zero crossings, a smoothing is necessary.

 

 

The appropriate smoothing filter, from among the many possibilities described in Section 9.4, should according to Canny have the following properties:

 

1.                 In the frequency domain, (u,v) or (,), the filter should be as narrow as possible to provide suppression of high frequency noise, and;

 

2.                 In the spatial domain, (x,y) or [m,n], the filter should be as narrow as possible to provide good localization of the edge. A too wide filter generates uncertainty as to precisely where, within the filter width, the edge is located.

 

The smoothing filter that simultaneously satisfies both these properties--minimum bandwidth and minimum spatial width--is the Gaussian filter described in Section 9.4. This means that the image should be smoothed with a Gaussian of an appropriate  followed by application of the Laplacian. In formula:

 

 

where g2D(x,y) is defined in eq. (93). The derivative operation is linear and shift-invariant as defined in eqs. (85) and (86). This means that the order of the operators can be exchanged (eq. (4)) or combined into one single filter (eq. (5)). This second approach leads to the Marr-ildreth formulation of the "Laplacian-of-Gaussians" (LoG) filter :

 

 

where

 

 

Given the circular symmetry this can also be written as:

 

 

 

This two-dimensional convolution kernel, which is sometimes referred to as a "Mexican hat filter", is illustrated in Figure 55.

 

(a) -LoG(x,y) (b) LoG(r)

 

Figure 55: LoG filter with  = 1.0.

 

 

*PLUS-based procedure - Among the zero crossing procedures for edge detection, perhaps the most accurate is the PLUS filter as developed by Verbeek and Van Vliet . The filter is defined, using eqs. (121) and (122), as:

 

 

 

Neither the derivation of the PLUS's properties nor an evaluation of its accuracy are within the scope of this section. Suffice it to say that, for positively curved edges in gray value images, the Laplacian-based zero crossing procedure overestimates the position of the edge and the SDGD-based procedure underestimates the position. This is true in both two-dimensional and three-dimensional images with an error on the order of (/R)2 where R is the radius of curvature of the edge. The PLUS operator has an error on the order of (/R)4 if the image is sampled at, at least, 3x the usual Nyquist sampling frequency as in eq. (56) or if we choose  >= 2.7 and sample at the usual Nyquist frequency.

All of the methods based on zero crossings in the Laplacian must be able to distinguish between zero crossings and zero values. While the former represent edge positions, the latter can be generated by regions that are no more complex than bilinear surfaces, that is, a(x,y) = a0 + a1*x + a2*y + a3*x*y. To distinguish between these two situations, we first find the zero crossing positions and label them as "1" and all other pixels as "0". We then multiply the resulting image by a measure of the edge strength at each pixel. There are various measures for the edge strength that are all based on the gradient as described in Section 9.5.1 and eq. . This last possibility, use of a morphological gradient as an edge strength measure, was first described by Lee, aralick, and Shapiro and is particularly effective. After multiplication the image is then thresholded (as above) to produce the final result. The procedure is thus as follows :

 

Figure 56: General strategy for edges based on zero crossings.

 

The results of these two edge finding techniques based on zero crossings, LoG filtering and PLUS filtering, are shown in Figure 57 for images with a 20 dB SNR.

 

 

a) Image SNR = 20 dB  b) LoG filter  c) PLUS filter

 

 

Figure 57: Edge finding using zero crossing algorithms LoG and PLUS. In both algorithms  = 1.5.

 

Edge finding techniques provide, as the name suggests, an image that contains a collection of edge pixels. Should the edge pixels correspond to objects, as opposed to say simple lines in the image, then a region-filling technique such as eq. may be required to provide the complete objects.