Актуальность проблемы. Развитие горнодобывающей промышленности харак¬теризуется переходом на более глубокие горизонты и усложнением условий ведения горных работ, что может привести к резкому снижению уровня безопасности труда шахтеров. Актуальность проблемы охраны труда в шахте предъявляет высокие требования к надежности и эффективности функционирования шахтных систем и особенно важной из них — шахтной вентиляционной системы (ШВС). Нарушения нормального функционирования ШВС могут приводить к самым тяжелым последствиям как экономического, так и социального характера.
        Вентиляционные сети шахт представляют собой совокупность большого количества подземных выработок, отличающихся разнообразием параметров, влияющих на аэродинамику этих сетей. Эти параметры постоянно меняются, следовательно, меняется и аэродинамика сетей. Этот процесс определяется совокупностью многочисленных геологических, технологических и технических факторов, большинство из которых носят стохастический (случайный) характер. Действие этих факторов обусловливает стохастическую динамику структуры и параметров ШВС, которая в настоящее время не учитывается в процессе отработки шахтного поля. Вследствие этого, в функционировании ШВС появляются нарушения вентиляции, т.е. отказы системы.

        Общая постановка проблемы. Назначение вентиляции в шахте — подавать необходимое количество воздуха с определенной величиной депрессии вентилятора в шахту. Исходя из назначения вентиляции шахт, можно сказать, что функция ШВС заключается в непрерывном обеспечении всех потребителей воздухом в количестве и по качеству, требуемым для поддержания нормативного, т.е. удовлетворяющего требованиям правил безопасности состояния шахтной атмосферы. Поэтому надежная работа ШВС заключается в свойстве сохранять в процессе функционирования способность обеспечивать требуемое воздухораспределение в сети горных выработок. Это означает, что в процессе функционирования ШВС в любой момент времени t в каждой i-й выработке (ветви сети) фактический расход воздуха Q_i(t) должен находиться в интервале допустимых значений. Значение нижней (левой) границы этого интервала Q_i(t) равно значению максимальной из следующих двух величин: Q_i(t)– расход воздуха, требуемый по газовому, тепловому и пылевому факторам, а также по количеству работающих на объекте людей; Q_i(s) – расход воздуха, требуемый по минимально допустимой скорости его т.е.

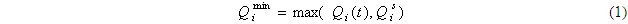
        Таким образом, признак надежности ШВС – выполнение в любой момент времени следующего неравенства:


n_b – количество ветвей шахтной вентиляции.

        Выходным эффектом ШВС является степень соответствия фактического воздухораспределения требуемому. Выход фактического расхода воздуха за границы интервала его допустимых значений означает отказ ШВС. Чем больше отклонение факти-ческого расхода воздуха Q от границ интервала его до¬пустимых значений , тем менее эффективно функционирует ШВС. Количество подаваемого воздуха в шахту зависит от следующих процессов: очистные работы, проходка выработок, погашение выработок, замена и добавление ГВ, аэродинамическое старение выработок, изменение потребностей в воздухе. В зависимости от перечисленных процессов, между моментами времени t_j-1 и t_j могут произойти некоторые события. Учитывая сложный процесс функционирования вентиляционных систем в шахтах, ограничим их в данной работе и рассмотрим процессы, протекающие при очистных работах.

        Случайные изменения во времени скоростей подвигания забоев могут быть как постепенными (вследствие непрерывных отклонений фактических значений параметров технологического процесса от их проектных значений), так и внезапными (из-за отказа оборудования или геологических нарушений). Стохастичностью скоростей подвигания забоев обусловлены также постепенные случайные изменения параметров ШВС, как изменения сопротивлений выработок вследствие изменения их длин в процессе отработки шахтного поля. Кроме того, постепенными изменениями параметров ШВС являются изменения сопротивления выработок в результате их аэродинамического старения (зажатие выработок, ухудшение со временем герметичности вентсооружений). Внезапные изменения параметров ШВС представляют собой изменения сопротивлений элементов сети вследствие их разрушения (обрушения выработок, разрушения вентсооружений). Постепенные случайные изменения параметров ШВС будем называть «старение» ее элементов. Внезапные же изменения, т.е. «разрушения» в работе рассматриваться не будут.

         Решение задачи и результаты исследования. Для разработки модели ШВС был выбран один из методов математического моделирования надежности технических систем – имитационное моделирование, предметом которого является сам процесс функционирования ШВС, т.е. поведение системы в ее развитии. Достоинством имитационного метода является высокая степень адекватности модели и всеобъемлющий анализ поведения системы, а недостатки — сложность вычислительного процесса.

         Решение задач регулирования подачи воздуха на математической модели вентиляционной системы позволяет производить большое количество экспериментов в сравнительно короткие промежутки времени, а также анализировать состояние вентиляционной системы при изменении ее параметров, причем диапазон изменения параметров практически неограничен (т. е. на математической модели возможно смоделировать практически любую ситуацию). Постепенное изменение во времени сопротивления выработки вследствие ее аэродинамического старения представляет собой некоторый случайный процесс R(t). Характеристиками случайного процесса являются его закон распределения (при исследовании многих технических объектов было предположено, что интенсивности потоков отказов и восстановлений постоянны, т.е. случайные потоки отка¬зов носят установившийся характер), математическое ожидание m(t), дисперсия σ (t²; ) и корреляционная функция K(t). Для получения оценок статистических характеристик необходимо провести анализ данных, полученных путем проведения экспериментальных исследований. Экспериментальные исследования заключаются в том, что на схожих по горно-геологическим и горнотехническим факторам лавах выделяются группы выработок, на которых проводятся измерения. Изменение во времени сопротивления конкретного наблюдаемого объекта представляет собой отдельную реализацию случайного процесса старения R(t), который характерен для элементов ШВС аналогичного с наблюдаемым объектом подтипа, далее производится измерения значений каждой из реализаций случайного процесса старения выработок. Экспериментальные исследования в шахтах достаточно сложны и требует больших материальных и технических затрат, поэтому в работе будем использовать статистические данные, полученные ранее для подобных систем. На основе экспериментальных данных, усреднением по каждой выборке, т.е. по реализациям, определим выборочное среднее mR(t)≠ и выборочную дисперсию D_r(t_j).

         Корреляционная функция случайного процесса старения R(t) в силу его нестационарности (поскольку даже его математическое ожидание m_R(t) ≠ const является функцией двух переменных K_R(t', t"). Оценка корреляционной функции такого вида - достаточно сложная и трудоемкая задача. Однако исходный процесс R(t) можно преобразовать к стационарному виду, рассматривая так называемый нормированный процесс старения R₀(t). При этом случайные величины R_i(tj) в каждом временном отсчете t_j преобразуются следующим образом:

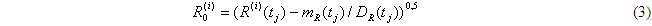
        Полученная последовательность случайных величин является стационарной и, следовательно, корреляционная функция нормированного процесса старения R0(t) является функцией одного переменного – временного интервала между отсчетами τ = (t', t") , т.е. K_R(t', t") = K₀(τ ), и ее оценка определяется простым усреднением по реализациям. Однако для тех моментов времени tj , для которых количество наблюдаемых реализаций n_j процесса R(t) мало, оценка корреляционной функции, получаемая усреднением по реализациям, будет иметь низкую точность. Предполагая эргодичность нормированного случайного процесса старения R₀(t), можно получить более точную оценку, используя вместо усреднения по реализациям усреднение по времени какой-нибудь одной i -й из реализаций:

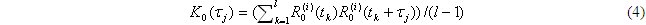
        Правомерность допущения об эргодичности процесса R₀(t) обусловлена стремлению к нулю при τ больше бесконечности его корреляционной функции. Окончательно оценка корреляционной функции K_R(t', t") (t" = t'+ τ ) исходного процесса старения R(t) имеет вид:

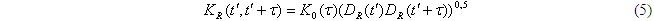
        Вид интерполирующих моделей m_R(t), σR(t) и K0(j), которые аппроксимируют полученные в дискретные моменты времени t_j оценки статистических характеристик с помощью аналитических функций, выбран исходя из следующего. Случайный процесс старения выработок R(t) «зашумлен» потоком ее периодических профилактических ремонтов (перекреплений), поэтому изменение во времени статистических характеристик процесса R(t) так же должно носить периодический характер. Поэтому в выражениях для mR(t), σR(t) и K₀(j), должны присутствовать тригонометрические функции.

        Исходя из вышесказанного, функции, аппроксимирующие статистические характеристики процесса старения выработок R(t), выберем в виде:

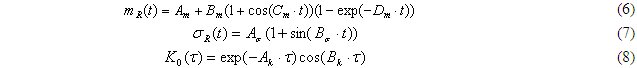
        Входящие в выражения (6)-(8) коэффициенты A, B, C и D определяются методом наименьших квадратов. Этот метод является одним из наиболее распространенных приемов статистической обработки экспериментальных данных, относящихся к различным функциональным зависимостям физических величин друг от друга. В том числе, он применим к линейной зависимости и позволяет получить достоверные оценки ее параметров. Выбранные интерполирующие модели (6) - (8) удовлетворительно описывают экспериментальные оценки статистических характеристик m_R(t), σR(t) и K₀(τj ).

         Кроме оценок математического ожидания, среднеквадратического отклонения и корреляционной функции модель случайного процесса старения выработок требует знания его закона распределения. Для определения вида закона распределения этого случайного процесса для различных его временных сечений t_j построим гистограммы. Затем программным путем оценим на соответствие плотностям девяти наиболее распространенных законов распространения с помощью критерия согласия Колмогорова – Смирнова при уровне значимости a = 0,05. Для всех классификационных групп выработок процесс старения R(t) имеет логнормальный закон распределения с плотностью распределения вида:

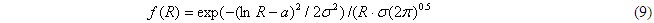
         Параметры логнормального закона распределения определяются по оценкам статистических характеристик процесса mR и σR следующим образом:

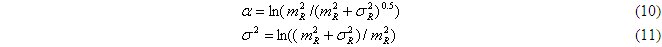
         Случайный процесс аэродинамического старения выработок R(t) и его статистические характеристики (6) - (11) отражают постепенные изменения сопротивления выработок. На основе полученных оценок статистических характеристик старения выработок мы сможем промоделировать случайный процесс старения выработки, используя одни из методов моделирования стационарных нормальных случайных процессов. В последнее время для стационарных нормальных случайных процессов найдены весьма экономичные моделирующие алгоритмы. Рассмотрим один из алгоритмов моделирования стационарных нормальных случайных процессов, а основу которого положено линейное преобразование стационарной последовательности x(t_j) независимых случайных чисел (дискретный белый шум) в последовательность y(t_j), имеющий заданный коэффициент корреляции K(τ). При этом оператор линейного преобразования представляет собой рекуррентную зависимость, которая по заданному виду коэффициента корреляции K(τ), значениям m(t_j), дисперсия σ(tj), а так же значениям процесса в предыдущие моменты времени y(t_j-k) определяется «постаревшее» значение (одно из возможных) процесса в следующий момент времени y(t_j). При этом оператор линейного преобразования записывается либо в виде скользящего суммирования с некоторым весом сk= c[k]

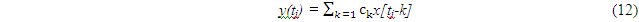
         Вид корреляционной функции случайного процесса, моделируемого с помощью (12) определяется набором значений параметров ak и bk и их количеством, которое обычно невелико. Алгоритмы (12) отличается простотой и позволяют формировать дискретные реализации случайных процессов сколь угодно большой длины.          Вывод: в рамках детерминированной модели системы, принятой в традиционных методах расчета вентиляции, невозможен адекватный учет стохастической динамики функционирования ШВС, которая и обуславливает отказы системы. Поэтому необходимым является учитывать изменения аэродинамических параметров выработок в рамках стохастической модели. Одним из основных этапов моделирования процесса старения выработок является получение его статистических оценок.

        
Список литературы
1. Ушаков В.К, «Надежность и эффективность шахтных вентиляционных систем», 2003 г.
2. Емелин П.В. «Теоретические проблемы решения задач регулирования воздухораспределения в шахтных вентиляционных системах», 2005 г.
3. Кельтон В., Лоу Л., «Имитационное моделирование», Москва, 2004 г.