Пересечение луча и треугольника

Фролов В., Фролов А.
Ray-tracing.ru

Источник: http://www.ray-tracing.ru/articles213.html

Аннотация

Введем следующие обозначения: P - origin луча, v - его направление. v0,v1,v2 - вершины треугольника. z - точка пересечения. t - рассточние от точки вылета луча до точки пересечения луча и треугольника. u,v,t1 - барицентрические координаты. Барицентрические координаты представляют собой отношения площадей маленьких треугольников к болшому (рис. 1.).

X u := u/S, v := v/S, t1 := t1/S

X t1 = 1 – u - v

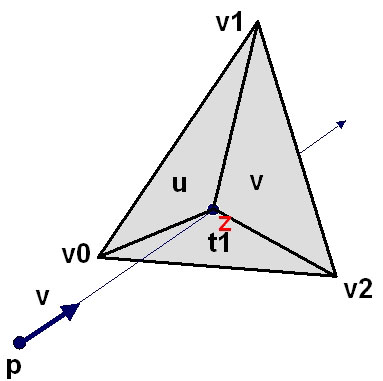
Рисунок 1 - Пересечение луча и треугольника

Барицентрический тест (fast minimal storage ray triangle intersection)

Это самый известный тест на пересечение луч-треугольник. Имея 3 точки на плоскости, можно выразить любую другую точку через ее барицентричечкие координаты. Первое уравнение берется просто из определения барицентрических координат, выражая точку пересечения z. С другой стороны, эта же точка z лежит на прямой. Второе уроавнение таким образом, это просто параметрическое уравнение пямой. Приравняв правые части уравенний 1 и 2 получаем третье уравнение, которое по сути является системой 3 уравнений (p,v,v1,v2,v3 - векторы) с 3 неивестными (u,v,t).

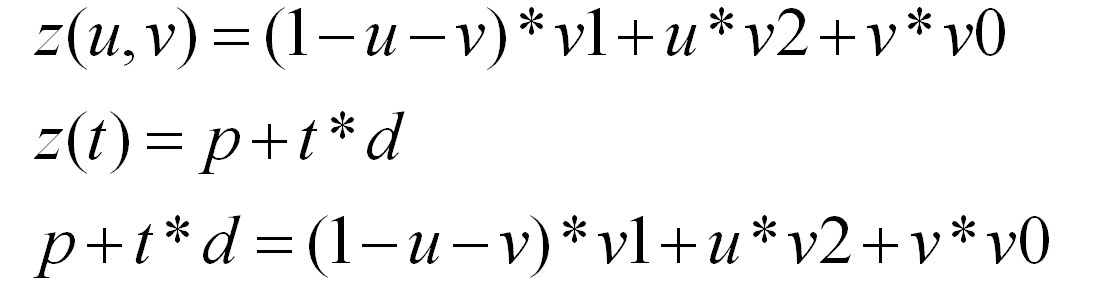
Проведя алгебраические преобразования получми ответ в следующем виде:

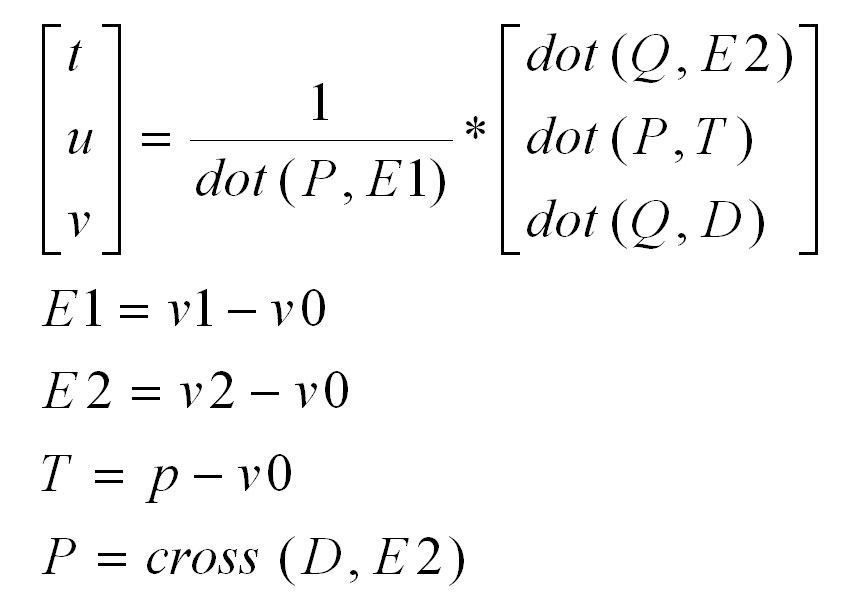
Юнит тест (Woop's unit test)

Основная идея данного алгоритма заключается в том, чтобы посчитать матрицу перобразования его в некий единичный треугольник (отсюда название) с вершинами (1,0,0); (0,1,0); (0,0,0); Во время подсчета пересечения луч преобразуется этой матрицей в пространство, где треугольник имеет единичное представление. После преобразования вычислить пересечение намного проще, так как нужно считать пересечение с заранее известным треугольником (1,0,0); (0,1,0); (0,0,0);. Пусть задан треугольник с вершинами A,B,C.

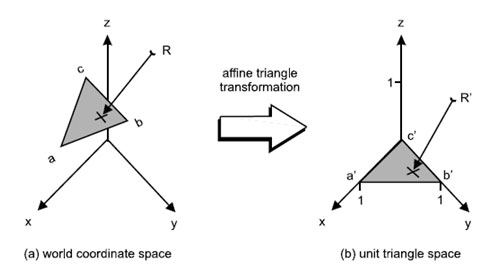
Рисунок 2 - Афинное преобразование треугольника в пространство, где он имеет единичное представление.

Рассмотрим преобразование T_∆^-1:

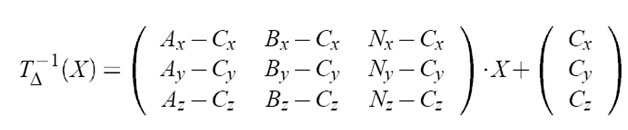
Если применить данное преобразование к треугольнику (1,0,0); (0,1,0); (0,0,0); то получим исходный треугольник.

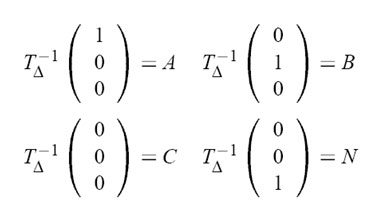
Для того чтобы найти нужное нам преобразование необходимо дополнить матрицу T_∆^-1 до 4x4 (добавить еще одну строчку (0,0,0,1)) и найти обратную матрицу. Это будет соответствовать обратному T_∆^-1 преобразованию. После необходимо лишь умножить луч на полученную матрицу и посчитать пересечение с единичным треугольником.


float3 o = mul3x4(m, ray_origin);
float3 d = mul3x3(m, ray_direction);
float t = -o.z/d.z;
float u = o.x + t*d.x;
float v = o.y + t*d.y;

Функция mul3x4 выполняет умножение подматрицы 3x3 на трехмерный вектор и добавляет к результату последний столбец (3 его компоненты). Функция mul3x3 просто умножает подматрицу 3x3 на трехмерный вектор.

Немного об эффективности

Несмотря на то, что юнит тест делает немного меньше вычислений (в худшем случае), с алгоритмической точки зрения он менее эффекивен. Причина заключается в том, что в юнит-тесте сначала вычисляется координата t а потом уже u и v. Как правило, если в сцене много мелких треугольников, именно по кооринатам u и v можно быстро отбросить те треугольники, которые заведомо не пересекаются.

Основное достоинства юнит-теста заключается в том, что он позволяет экономить регистры графического процессора при реализации алгоритма на GPU. Причина по которой данный тест позволяет экономить регистры заключается в том, что можно умножать матрицу последовательно по строкам и не хранить ее всю на регистрах. Сначала нужно прочитать из памяти третью строчку матрицы, умножить ее (как скалярное произведение двух векторов) на луч и получить координату t. Если она лежит в требуемом интервале, можно прочитать первую и вторую строчки и получить координаты u и v соответственно.