Курейчик В.М., Родзин С.И.
Эволюционные вычисления, синонимом которых в зарубежной литературе является термин «evolutionary computation», доказали свою эффективность как при решении трудноформализуемых задач искусственного интеллекта (распознавание образов, кластеризация, ассоциативный поиск), так и при решении трудоемких задач оптимизации, аппроксимации, интеллектуальной обработки данных. К преимуществам эволюционных вычислений относятся адаптивность, способность к обучению, параллелизм, возможность построения гибридных интеллектуальных систем на основе комбинирования с парадигмами искусственных нейросетей и нечеткой логики. Многообещающей выглядит предпосылка создания единой концепции эволюционных вычислений, включающих генетические алгоритмы, генетическое программирование (ГП), эволюционные стратегии и эволюционное программирование (ЭП). По мнению многих исследователей, эти парадигмы являются аналогами процессов, происходящих в живой природе и на практике доказавших свою непримитивность. Один из пионеров эволюционных вычислений Л.Фогель вообще видит теорию эволюции и самоорганизации как базовую концепцию для всех интеллектуальных процессов и систем, значительно расширяющую сферу применения традиционной парадигмы искусственного интеллекта. Даже если это не так, и в природе происходит реэволюция, никто не может сказать, что алгоритмы эволюционных вычислений неверны.
Поскольку концепция эволюционных вычислений должна быть основана на некоторых формализованных принципах естественного эволюционного процесса, то возникают вопросы о методологических различиях и сфере применения основных форм эволюционного моделирования.
Результаты сравнительного анализа известных форм эволюционных алгоритмов показывают определенные методологические различия между ними [1]. Эти различия касаются формы представления целевой функции и альтернативных решений, операторов рекомбинации, мутации и вероятностей их использования, стратегии селективного отбора и методов повышения эффективности эволюционных вычислений путем адаптации.
Методологические различия между разными формами эволюционных вычислений, тем не менее позволяют говорить о базовых постулатах, таких как универсальность и фундаментальность, присущих эволюции независимо от формы и уровня абстракции модели. Указанная общность может быть выражена в виде следующей схемы абстрактного эволюционного алгоритма [2]:
Решающим обстоятельством для оценки практической пригодности и результативности эволюционного алгоритма являются скорость (время, необходимое для выполнения заданного пользователем числа итераций) и устойчивость поиска (способность постоянно от поколения к поколению увеличивать качество популяции устойчивость к попаданию в точки локальных экстремумов).
Предпринятая в [3] попытка сравнительного анализа конкурирующих эвристических алгоритмов с точки зрения их результативности, даже при том, что NFL-теорема не учитывает время решения оптимизационной задачи, имеет два важных практических следствия:
С этой точки зрения эволюционные вычисления обладают следующими достоинствами и недостатками.
Достоинства эволюционных вычислений:
Недостатки эволюционных вычислений:
Таким образом, сравнительный анализ показывает, что эволюционные вычисления наименее подходят для решения задач, в которых требуется найти глобальный оптимум; имеется эффективный неэволюционный алгоритм; переменные, от которых зависит решение независимы; для задачи характерна высокая степень эпистазии (одна переменная подавляет другую); значения целевой функции во всех точках, за исключением оптимума, являются приблизительно одинаковыми. Принципиально подходящими для решения с помощью эволюционных вычислений являются задачи многомерной оптимизации с мультимодальными целевыми функциями, для которых нет подходящих неэволюционных методов решения; стохастические задачи; динамические задачи с блуждающим оптимумом; задачи комбинаторной оптимизации; задачи прогнозирования и распознавания образов.
Рассмотрим подробнее две относительно малоисследованные формы эволюционных вычислений: генетическое и эволюционное программирование.
Проблемы компьютерного синтеза программ стали одним из направлений искусственного интеллекта примерно в конце 50-х годов. Интерес исследователей к данной проблематике резко возрос благодаря работам Дж. Коза, посвященным генетическому программированию [6] и направленным на решение задач автоматического синтеза программ на основе обучающих данных путем индуктивного вывода.
Хромосомы или математические выражения, которые автоматически генерируются с помощью генетических операторов, являются компьютерными программами различной величины и сложности. Программы состоят из функций, переменных и констант. Исходная популяция P(0) хромосом в ГП образуется стохастически и состоит из программ, которые включают в себя элементы множества проблемно-ориентированных элементарных функций (function set: +, , ?, *, %, sin, сos, log, or, and, for, do-until и пр., а также любая другая функция из предметной области задачи), проблемно-ориентированные переменные и константы (terminal set: ephemeral random – константы регрессионных функций с коротким временем жизни; T, Nil– булевы константы; вещественные константы принимающие значение на отрезке [-1.000; 1.000] с шагом 0.001). Множества function set и terminal set являются основой для эволюционного синтеза программы, способной наилучшим образом решать поставленную задачу. Одновременно устанавливаются правила выбора элементов из указанных множеств в пространстве всех потенциально синтезируемых программ, структура которых имеет древовидную форму.
Первоначально в исследованиях по ГП применялся язык LISP, обладающий всеми необходимыми для синтеза ГП-структур свойствами, однако в настоящее время наряду с LISP используются языки C, Smalltalk, C++.
Стартовыми условиями для ГП являются установка множеств terminal set и function set; определение подходящего вида функции соответствия (fitness-function); установка параметров эволюции; определение критерия останова моделирования эволюции и правил декодирования результатов эволюции.
Способом оценки качества функции соответствия в ГП является среднеквадратичная ошибка (чем она меньше, тем лучше программа) или критерий «выигрыша», согласно которому выигрыш определяется в зависимости от степени близости к корректному значению математического выражения. Размер популяции ? в ГП обычно составляет несколько тысяч программ. Для максимального числа генераций tmax используется значение tmax=51.
Рассмотрим подробнее процедуру ГП.
Проиллюстрируем рассмотренную процедуру на примере вычисления разности объемов двух параллелепипедов. Пусть два параллелепипеда задаются шестью независимыми переменными L1,B1,H1,L2,B2,H2 и одной зависимой переменной D. Для получения корректных значений величины D установим следующие стартовые условия:
В табл. 1 представлены 10 различных вариантов исходных значений для шести независимых переменных, а также разность объемов D= L1*B1*H1-L2*B2*H2.
Таблица 1
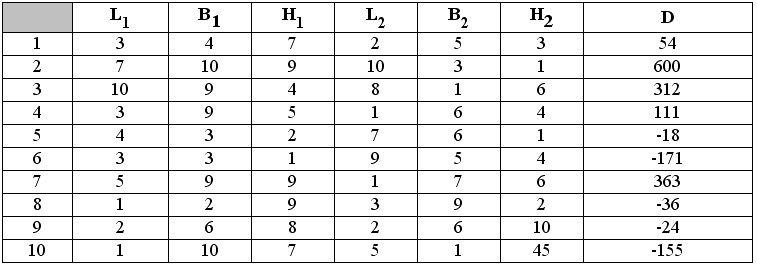
Исходные данные для вычисления разности объемов двух параллелепипедов
В результате моделирования эволюции для популяции P(0) лучшее значение D=783, что соответствовало следующему выражению:
(*(?(?B1L2)(?B2H1))(+(?H1H1)(*H1L1))) или H1L1(B1+H1?B2?L2).
Видно, что в данном математическом выражении отсутствует переменная H2 и оно мало похоже на корректное решение. Далее, лучшие значения D в популяциях P(1)-P(6) имели значения 778, 510, 138, 117, 53, 51 соответственно. Лучшая программа на восьмом этапе эволюции дала значение D, равное 4.44, что соответствовало LISP-выражению следующего вида:
(?(?(*(*B1H1)L1)(*(*L2H2)B2))(%(+B1L1)(?(?L1B2)(+(+B2L2)(*L2B2)))))
или B1H1L1?B2H2L2?(B1+L1)/(L1?2B2?L2?L2B2).
Видно, что, за исключением последнего ошибочного терма, данное выражение соответствует корректному решению. Наконец, на 11-м шаге эволюции была получена правильная программа вида:
(?(*(*B1H1)L1)(*(*L2H2)B2)) или L1B1H1?L2B2H2.
К перспективным направления развития ГП следует отнести работы по так называемым автоматически определяемым функциям (ADF), идея которых состоит в повышении эффективности ГП за счет модульного построения программ, состоящих из главной программы и ADF-модулей, генерируемых в ходе моделирования эволюции. До начала эволюции определяется структура программы, число ADF-модулей и параметры каждой ADF. Все вершин данной структуры имеют свой номер, список аргументов включает отдельные локальные переменные, которые определяются при вызове ADF. Задание функции главной программы завершает установку общей программы. Настройка ADF (их число, аргументы и т.п.) зависит от решаемой задачи, имеющихся вычислительных ресурсов и предварительного опыта. Отметим также необходимость типизации вершин дерева, иначе при выполнении оператора кроссинговера могут быть синтезированы синтаксически некорректные решения.
Эксперименты с использованием ADF для ранее рассмотренной задачи о параллелепипедах показали что с точки зрения вычислительной трудоемкости и структурной сложности преимущество за ГП без ADF.
Однако имеется целый ряд задач, свидетельствующих об обратном. Рассмотрим одну из них, связанную с проверкой на четность. Пусть булева функция, зависящая от пяти аргументов (D0,D1,D2,D3,D4), принимает значение T, если четное число аргументов принимают значение «истина», в противном случае, булева функция принимает значение Nil (константа, обозначающая список, в котором нет ни одного элемента); 32 возможных комбинации аргументов служат основой для оценки ГП с ADF и без ADF.
Для ГП без ADF и с ADF устанавливаются одинаковые стартовые условия и параметры эволюции: функция соответствия определяется числом совпадений значений исходной функции со значениями, выдаваемыми ГП; ?=16000; программа останавливается, если число совпадений равно 32.
Результаты моделирования однозначно свидетельствуют о преимуществе ГП с ADF как по структурной сложности решений, так и по вычислительной трудоемкости.
Другим перспективным направлением в ГП является применение в качестве оператора поиска не только кроссинговера, но и мутации, а также реализацию ГП на транспьютерных вычислительных системах. Существенное увеличение быстродействия ГП может быть получено и на последовательных машинах. В частности, реализация ГП на языке C увеличивает скорость ГП примерно на два порядка, а реализация ГП в машинных кодах ? примерно на три порядка в сравнении с LISP-реализациями.
Авторы [8], исследуя решения различной длины, получаемые с помощью ГП, обратили внимание на так называемый эффект «компрессионного давления», которым обладают решения с малой структурной сложностью. Программы, генерируемые по методу ГП, как уже отмечалось выше, зачастую содержат «лишние» блоки, не влияющие на функциональные возможности программы и на целевую функцию. В генетике это соответствует понятию интрона, который является нечувствительным к кроссинговеру. Принято считать, что применение кроссинговера носит деструктивный характер, если целевая функция ухудшается. Следовательно, для программы с относительно большим значением структурной сложности, но содержащей много интронов, опасность деструктивного воздействия кроссинговера заметно уменьшается. С учетом этого, а также принимая во внимание известную Schema-теорему Дж.Холланда, приведем следующую последовательность рассуждений.
Обозначим через Се(аi) эффективную сложность программы ai (i=1,2,…?), через Сa (ai) абсолютную сложность программы аi, через pc – вероятность применения кроссинговера, а через pd –вероятность того, что применение кроссинговера приведет к деструктивному эффекту, причем pd=0, если кроссинговер проводится с интроном. Пусть Ф(ai) – значение функции соответствия программы ai; ?(ai)- среднее значение функций соответствия всех программ в популяции P(t). Если применяется пропорциональная селекция, то нижняя оценка Ai(t+1) «доли» программы ai в популяции P(t+1) примерно равна
Ai(t+1) ? Ai(t)·?(ai)/[?(t)]·(1?pc·Се(аi)·pdi/ Сa (ai)) = = Ai(t)·? ?(ai)?pc·?(ai) Се(аi)·pdi/ Сa (ai) ?,
где выражение в скобках представляет собой функцию ?e(ai) эффективной сложности программы:
?e(ai) = ?(ai)?pc·?(ai) Се(аi)·pdi/ Сa (ai),
которая соответствует вкладу программы ai в следующую популяцию P(t+1). Отсюда следует, что репродуктивные шансы некоторой программы ai тем выше, чем меньше отношение между эффективной и абсолютной сложностью программы. Достигнуть этого можно двумя путями.
Первый заключается в увеличении абсолютной сложности путем добавления интронов, второй – в поиске простых решений. Эмпирические данные [1], подтверждают приведенные выше соображения:
Теоретически обоснованное и эмпирически наблюдаемое явление «компрессии» таит в себе опасность преждевременной сходимости ГП к субоптимальным решениям.
Это означает, что применение Scheme-теоремы для описания динамики эволюционного процесса является сильно упрощенным подходом. Необходим более тщательный анализ не только статических, но и динамических особенностей различных форм представления хромосом в популяции.
Идеи эволюционного программирования при компьютерном синтезе интеллектуальных автоматов, способных инновационным образом реагировать на стимулы, поступающие из внешней среды, стали одним из направлений искусственного интеллекта после выхода работы [9]. Эти идеи выглядят сегодня актуальными с позиций теории многоагентных систем, искусственной жизни, коллективного поведения, помогают лучше понять феномен интеллекта и взаимодействия между агентами.
Прежде чем обсуждать концепцию, особенности и механизм ЭП, уточним принципиальные аспекты, отличающие ЭП от ГП. В ЭП популяция рассматривается как центральный объект эволюции. ЭП исходит из предположения о том, что биологическая эволюция является, в первую очередь, процессом приспособления на поведенческом уровне, а не на уровне таких генетических структур как хромосомы. Особь в ЭП-популяции отражает характер поведенческой реакции, вид общения и пр. Этот уровень абстракции в природе не предусматривает рекомбинации. Поэтому в ЭП отсутствует оператор кроссинговера, также как и некоторые другие операторы, используемые в ГП (например, инверсия). Мутация в ЭП является единственным оператором поиска альтернативных решений на уровне фенотипа, а не на уровне генотипа, как в ГП.
Рассмотрим стандартную форму ЭП-алгоритма. Пусть стоит задача минимизации функции F(а1,…, аn), зависящей от n непрерывных переменных: F: Rn > R.
В ЭП отсутствуют ограничения на вид целевой функции и представление альтернативных решений, кроме тех, которые вытекают из постановки задачи. Вещественные переменные обычно представляются в виде вектора A=(а1,…, аn), который в ЭП соответствует отдельной особи. Тогда стандартная форма ЭП-алгоритма включает следующие этапы.
1) Инициализация. На этапе инициализации случайным образом генерируется популяция Р(0), состоящая из ? особей Ai (i=1,2,…, ?). Рекомендуемое значение размера популяции ??200. Значение элемента aj для каждой особи Ai устанавливается случайно с помощью равномерного распределения на интервале [lj , rj ] Є R, lj < rj . Границы интервала lj , rj имеют значение лишь на этапе инициализации. В ходе дальнейшей эволюции пространство поиска в принципе является неограниченным. Стандартная форма ЭП предполагает решение оптимизационной задачи, в которой оптимальное значение равно 0, lj =?50, rj =50.
2) Оценка решения. Каждая особь Ai определяет функцию соответствия ?(Ai), которая зачастую равна значению целевой функции (?=F, хотя в общем случае они могут и не совпадать). В случае несовпадения функции соответствия и целевой функции, значение ? преобразуется с помощью некоторой случайной величины ?i. Например, если результирующее значение функции соответствия получилось отрицательным, то оно преобразуется путем скаляризации в положительное число. Таким образом, в общем случае считают, что ?(Ai)=?(F(Ai), ?i.).
Совокупность из ? особей образует множество родителей, необходимых для следующего этапа ЭП.
3) Генерация потомков. Этот этап выполняется ? раз (i=1,2…?) и включает в себя следующие действия.
3.1) Репликация путем копирования i-го родителя Ai=(а1,…, аn).
3.2) Мутация скопированного родителя путем сложения нормально распределенной случайной величины с нулевым математическим ожиданием и динамически изменяемым среднеквадратичным отклонением. Из родителя Ai возникает потомок A?i Стандартное отклонение («ширина мутации») полученной случайной величины зависит от родительского значения функции соответствия ?. При этом глобальный оптимум равен 0 (если это не так, то проводится соответствующее преобразование). Идея состоит в том, чтобы повысить эффективность процесса оптимизации путем сокращения «ширины мутации» при приближении к оптимуму. Значение переменной потомка определяется по формуле:
a?j = aj + sqrt(kj •?(Ai) + zj)•Nj (0, 1)
,kj –константа скалирования, ?(Ai) –значение функции соответствия родителя, zj -дисперсия, Nj (0, 1) –стандартная нормально распределенная величина, определяемая для каждого j=1,2,…n. Значения kj , zj (kj, zj ЄR+) являются параметрами ЭП и устанавливаются пользователем. В общем случае, число этих параметров равно 2•n. Однако на практике устанавливают kj=1, zj=0 (j=1,2,…n). Тогда квадратный корень (sqrt) в формуле для вычисления a?j упрощается и она принимает следующий вид:
a?j = aj + sqrt(?(Ai))•Nj (0, 1).
3.3) Оценка потомка происходит путем определения значения его функции соответствия ?(A?i)=?(F(A?i), ?i.), после чего потомок добавляется в популяцию, причем A?i > A??+i . При окончании этапа 3 размер популяции становится равным 2•?.
4) Случайная селекция. Селекция выполняется по соревновательному принципу, согласно которому каждый родитель или потомок попарно сравнивается с h противниками, причем hЄN (h?1) является параметром ЭП, устанавливается пользователем и обычно принимает значения от h=0.05? до h=0.1?. Противники выбираются случайно с помощью закона равномерного распределения. Победитель определяется путем попарного сравнения функций соответствия. Особь побеждает в соревновании, если ее функция соответствия по меньшей мере не хуже, чем у ее противника. Для представленной выше задачи минимизации число побед Wi i-ой особи (i=1,2,…2•?) определяется как Wi =?{1, если ?(Ai)? ?(Ad)}, причем суммирование ведется для d=1,2,…h и d?i является целочисленным значением равномерно распределенной в интервале [1, 2•?] случайной величины, которое для каждого d определяется заново. После этого все особи сортируются по убыванию числа побед (а не по значению функций соответствия). Лучшие особи образуют новую родительскую популяцию размером ?. При одинаковом числе побед преимущество получает особь с лучшим значением функции соответствия. Очевидно, что при таком механизме селекции «слабые» особи имеют некоторую отличную от нуля вероятность репродукции. С ростом значения параметра h селекция начинает принимать дискриминационный элитарный характер.
5) Критерий останова. В качестве критерия останова могут быть следующие заданные пользователем события:
a) достижение в ходе эволюции заданного числа поколений tmax ;
b) достижение заданного уровня качества, когда, например, значение функций соответствия всех особей в популяции превысило некоторое по
c) достижение заданного уровня сходимости, когда особи в популяции настолько подобны, что дальнейшее их улучшение происходит чрезвычайно медленно.
Параметры ЭП выбираются таким образом, чтобы обеспечить скорость работы алгоритма и поиск как можно лучшего решения.
В отличие от генетических алгоритмов, ЭП является относительно малоисследованной парадигмой моделирования эволюции. Из теоретических результатов внимания заслуживает доказательство асимптотической сходимости рассмотренной выше стандартной формы ЭП [10], основанное на теории марковских цепей. Доказательство приводится для случая, когда параметры kj , zj принимают значение 1 и 0 соответственно, а также справедливо ?(Ai)=F(Ai)>0. Представляется, что математический аппарат марковских цепей как модель описания стохастических процессов вполне подходит в качестве одной из фундаментальных основ для формирования единой концепции эволюционных вычислений. С помощью марковских цепей можно обосновать эффективность эволюционного процесса.
Одним из перспективных направлений практического развития идей ЭП является преодоление следующих проблем:
(1) Если глобальный оптимум функции соответствия отличается от 0, то это негативно влияет на устойчивость ЭП;
(2) Если значения функции соответствия являются очень большими, то поиск становится квазислучайным;
(3) Если пользователь не обладает информацией о глобальном оптимуме, то согласование и подбор функции скаляризации ? становится затруднительным;
(4) Необходимость установки 2•n значений параметров эволюции kj и zj выдвигает перед пользователем дополнительные оптимизационные трудности, даже если он использует стандартную установку (kj =1, zj =0).
Преодоление этих недостатков стандартной формы ЭП требует ее модификации с целью повышения адаптивных свойств ЭП. Рассмотрим возможные модификации ЭП в этом направлении.
Пусть популяция составляется не из векторов Ai (i=1,2,…, ?), а из векторов Ei = (Ai , ui ), где ui – вектор среднеквадратичного отклонения, элементы которого uj Є R+ (j=1,2,…n). Тогда речь может идти о следующих отличиях модифицированной ЭП от рассмотренных ранее этапов стандартной формы ЭП.
На этапе инициализации для каждого вектора Ai дополнительно образуется вектор ui на основе равномерного распределения в интервале [0, ?], где ?>0 является параметром эволюции (рекомендуемое значение ?=25), который требует адаптации к каждому конкретному классу задач. На этапе генерации потомков отличие состоит в операторе мутации. В частности, потомок E'i = (A'i , u'i ), где u'j = uj + uj?Nj (0,1), a'j = aj + u'jNj (0,1). Отметим, что, если коэффициент ? выбрать слишком большим, то величина u'j может стать отрицательной и тогда она заменяется на некоторое малое ?>0, что несколько противоречит идее адаптации. Если ? выбрать слишком малым, то проявляется тенденция замедления эволюции. Рекомендуемое значение ?=1/6 [Fog92a]. Заслуживает внимания и другая идея. Речь идет о программируемой мутации путем с использованием ковариационной матрицы, составленной из коэффициентов корреляции и подробно рассмотренной в [11] применительно к другой парадигме моделирования эволюции – эволюционным стратегиям.
Перспективным направлением диверсификации и адаптации ЭП является также изменение процедур генерации потомков и селекции. Например, на этапе генерации потомков из популяции с помощью закона равномерного распределения в интервале [1, ?] случайно выбирается родитель, из которого путем применения того или иного варианта оператора мутации получают потомка. Далее, потомок оценивается, добавляется в популяцию, размер которой становится равным (?+1), после чего производится детерминированная селекция путем исключения из популяции слабой особи.
До сих пор мы, в основном, предполагали, что популяция из ? родителей генерирует ? потомков, что придает определенную остроту процессу селективного отбора и положительно влияет на скорость ЭП при унимодальных функциях оптимизации. Однако многие практические задачи имеют комбинаторную природу, а переменные целевой функции являются дискретными. Для них представленная выше процедура мутации напрямую неприменима.
В частности, одним из наиболее объективных средств тестирования эволюционных алгоритмов для NP-полных комбинаторных проблем является задача о коммивояжере [7]. Приведем результаты тестирования ЭП для задачи о коммивояжере, предусматривающей обход 100 городов.
Каждая особь в популяции решений кодировалась перестановкой целых чисел от 1 до 100, определяющих номер города. Исходная популяция состояла из 50 случайно выбранных перестановок. Функция соответствия определялась как суммарная длина цикла, задаваемого порядком обхода коммивояжером всех городов и указанного в перестановке. Оператор мутации предусматривал случайный выбор в перестановке двух городов с их последующей взаимозаменой. Полученные таким образом 50 потомков и 50 родителей соревновались с пятью случайно выбранными контрагентами. Понятно, что каждая особь в таком соревновании может одержать максимум 5 побед. Однако победителем в единоборстве не всегда становилась особь с меньшим значением функции соответствия. Вместо этого задавалась вероятность победы в виде разности:
1 — (длина цикла особи/сумма длин циклов оцениваемой особи и контрагента).
Это означает, что у слабой особи имеется некоторый шанс победить в соревновании. Затем популяция из 100 особей сокращалась до 50 особей, имевших наибольшее число побед, после чего цикл эволюции повторялся вновь до останова. Сравнение полученных результатов с генетическим алгоритмом на основе PMX-операторов [10] о некотором преимуществе ЭП.
Роль ЭП в моделировании интеллектуального поведения агентов также может быть весьма плодотворной. Одним из наиболее объективных средств тестирования эволюционных алгоритмов для подобного рода проблем является классическая задача теории игр, называемая «дилеммой узников».
Эта задача служит неплохой моделью конфликтной ситуации, в которой интересы игроков (агентов) хотя и различны, но не являются антагонистическими. Игроками считаются два узника, находящиеся в предварительном заключении по подозрению в совершении преступления. При отсутствии прямых улик возможность их осуждения в значительной степени зависит от того, заговорят они или будут молчать. Если оба будут молчать, наказанием будет лишь срок предварительного заключения (потери каждого из узников составят 1 год). Если оба сознаются, то получат срок, учитывающий признание как смягчающее обстоятельство (потери каждого из узников в этом случае составят 3 года). Если же заговорит только один из узников, а другой будет молчать, то заговоривший будет выпущен на свободу (его потери равны 0), а сохранивший молчание получит максимально возможное наказание (его потери будут равны 5 лет). Эта конфликтная ситуация приводит к игре, в которой каждый из игроков имеет по две стратегии — молчать (М) или говорить (Г). Потери игроков описываются матрицей следующего вида:
| M | Г | |
| M | (1,1) | (5,0) |
| Г | (0,5) | (3,3) |
Ясно, что наиболее выгодным для них является молчание. Однако простое рассуждение показывает, что, не имея никаких контактов между собой, и к тому же не очень доверяя друг другу, каждый из узников, поразмышляв, придет к выводу, что нужно сознаваться.
Задачей ЭП является поиск такой игровой стратегии, которая позволит минимизировать средние потери при многократном повторении игровой ситуации. Следуя [Fog66], можно представить каждую совместную игровую стратегию одним из состояний конечного автомата. Множество возможных входных сигналов автомата при символьном представлении равно {(м/м), (м/г), (г/м), (г/г)}. Множеством выходов автомата являются символы {м, г}.
В ходе эксперимента размер исходной популяции ?=50, число ходов в игре — не менее 150, число состояний, переходы состояний, первый ход, а также выход автомата устанавливаются случайно. Каждый автомат копировался, над ним производилась мутация на базе равномерного распределения. В дальнейшем каждый автомат попарно сравнивался с 99 другими, причем в качестве функции соответствия выбирались ожидаемые средние потери. Хотя в игре возможна стохастическая селекция, предпочтительнее применять детерминированный отбор, согласно которому из 100 автоматов выбирались 50 лучших. Критерием останова в данной задаче являлось значение tmax =200. В табл. 2 в качестве иллюстрации приводится список возможных автоматных состояний и переходов между состояниями, полученный в ходе работы ЭП-алгоритма для задачи «дилемма узника».
Таблица 3
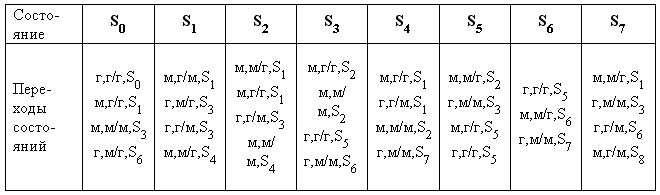
Здесь S0 - это стартовое состояние, входом которого являлось решение узника говорить («г»), а, например, запись в столбце S4 (г,г/м, S2 ) означает, что узник на очередном ходе принял решение говорить, на предыдущем ходе использовалась стратегия г/м, автомат из состояния S4 переходит в состояние S2. Эксперименты с автоматами показали, что примерно в течение первых 20 ходов преобладает стратегия молчания, хотя уже после 5-10 ходов начинает встречаться стратегия кооперативного поведения, которая в дальнейшем однозначно становится доминирующей.
ЛИТЕРАТУРА