Predicting patient arrivals to an accident and emergency department

S W M Au-Yeung
U Harder
E J McCoy
W J Knottenbelt

Source of information: http://prime.mines.edu/papers/tutorial-wsc05.pdf

ABSTRACT

   Objectives: To characterise and forecast daily patient arrivals into an accident and emergency (A&E) department based on previous arrivals data.
   Methods: Arrivals between 1 April 2002 and 31 March 2007 to a busy case study A&E department were allocated to one of two arrival streams (walk-in or ambulance) by mode of arrival and then aggregated by day. Using the first 4 years of patient arrival data as a "training" set, a structural time series (ST) model was fitted to characterise each arrival stream. These models were used to forecast walk-in and ambulance arrivals for 1–7 days ahead and then compared with the observed arrivals given by the remaining 1 year of "unseen" data.
   Results: Walk-in arrivals exhibited a strong 7-day (weekly) seasonality, with ambulance arrivals showing a distinct but much weaker 7-day seasonality. The model forecasts for walk-in arrivals showed reasonable predictive power (r=0.6205). However, the ambulance arrivals were harder to characterise (r=0.2951).
   Conclusions: The two separate arrival streams exhibit different statistical characteristics and so require separate time series models. It was only possible to accurately characterise and forecast walk-in arrivals; however, these model forecasts will still assist hospital managers at the case study hospital to best use the resources available and anticipate periods of high demand since walk-in arrivals account for the majority of arrivals into the A&E department.

   Accident and emergency (A&E) departments are being placed under increasing pressure to process a growing number of patients safely and quickly. This is evidenced by the national government target whereby 98% of patients must spend 4 h or less from arrival to admission, transfer or discharge[1], as well as an increase in the number of attendances to A&E departments and walk-in centres in England (with 16.5 million attendances in 2003 and over 18.9 million attendances in 2007[2]). Concurrently, in 2003–6, seven hospital trusts reported one or more A&E departments closed or downgraded, with one new A&E department opening[2]. For the remaining open A&E departments to be able to plan ahead for staffing and resource needs effectively, it is important to understand and characterise the nature of patient arrivals.
   There are many studies describing simulations of A&E departments (or emergency departments (EDs) in countries other than the UK) in which either a Poisson arrivals process is assumed or historical attendance is replicated[3-8].
   For current and future A&E simulations and models to be effective in providing insights into departmental improvements, they need to be parameterised with a realistic workload. Using Poisson arrivals or replicating historical arrivals is a much simplified view since, in the former case, it is known that demand for emergency care follows seasonal patterns, with higher numbers of attendances during the summer months but more critical care required over the winter months[9]; in the latter case, long-term trends are not accounted for.
   Other studies have attempted to characterize and forecast acute arrivals to hospitals using a number of different time series models including autoregressive (AR), moving average (MA) and autoregressive integrated moving average (ARIMA) models[10-12]. However, these studies consider only emergency admissions, ambulance arrivals or total arrivals without distinguishing between different patient arrival types.
   In this paper we present a new approach to A&E arrival predictions using power spectral density analysis and structural time series models. Structural time series (ST) models are particularly suited to data sets such as A&E arrival streams which exhibit seasonality and are not stationary (ie, the statistical properties of the data such as mean, variance and autocorrelation structure change over time). Furthermore, in contrast to previous work, we use separate time series models to characterise and forecast walk-in and ambulance arrivals as opposed to either modelling total arrivals[12] or only ambulance arrivals[10].
   This study is based on 5 years of pseudonymised patient arrivals data supplied by the A&E department of a high-acuity North London hospital with over 100 000 annual attendances and an admission rate of approximately 25%. Our goals were (1) to use "training" data to characterise each arrival stream by analysing its power spectrum and fitting an appropriate time series model and (2) to test predictive ability (in terms of predicting the number of daily walk-in and ambulance arrivals) of the time series models for each arrival stream using "unseen" data.

METHODS

   All patient arrivals to our case study A&E department from 1 April 2002 to 31 March 2007 were studied. Patients were classified either as ambulance arrivals (where electronic patient records indicate that the patient arrived via an ambulance) or walk-in arrivals (all other modes of patient arrival). This data set was then aggregated to get separate time series of ambulance and walkin arrivals by day. These two time series of daily arrivals were then further split into (1) "training" data consisting of the first 4 years (1456 days) of arrivals which was used to fit our time series models, and (2) "unseen" data consisting of the remaining 370 days of arrivals which was used to determine the accuracy of our model forecasts. All the time series models in this study were created and fitted using the R statistical software package[13]; the R scripts used in this study can be found at http://www.doc.ic.ac.uk/ ,swa02/ST.txt.
   Preliminary data analysis
   Plots of the "training" data of daily walk-in and ambulance arrivals are shown in fig 1. A power spectral density analysis, which describes how the power (strength) of a time series is distributed by frequency, was applied to these time series to determine the power of any periodicities present. The results of this frequency domain analysis are shown in fig 2. Walk-in arrivals show distinct peaks in the power spectrum corresponding to weekly (7-day) periodic behaviour in the data. The initial large peak at low frequency indicates an annual periodicity and the lower peaks (at 2- and 3-1/week frequencies) correspond to the harmonics of the main 7-day frequency. Ambulance arrivals exhibit a distinct but much weaker 7-day periodicity and also an annual periodicity. The different characteristics exhibited by the power spectra underline the need to use separate time series models for each arrival type.

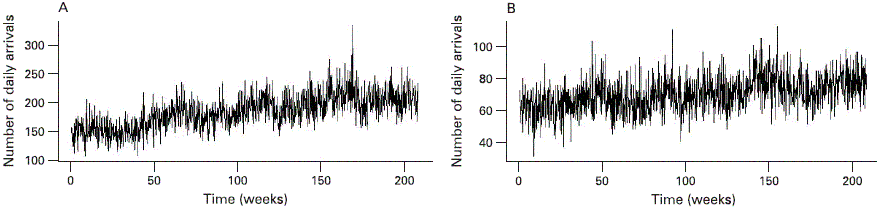Figure 1 Time series of (A) walk-in and (B) ambulance arrivals

Figure 2 Power spectra of the time series of (A) walk-in and (B) ambulance arrivals

   Two types of time series models were fitted: AR models[14-15] and ST models[16]. We considered AR models since they are often applied to time series exhibiting regularity. However, ST models were more suited to our needs as they (1) do not require preprocessing of the data to satisfy stationarity assumptions (unlike AR models); (2) allow us to explicitly incorporate seasonal factors and local linear trends; and (3) perform better for both the walk-in and ambulance arrival predictions in terms of root mean square error (RMSE) and Pearson’s productmoment correlation coefficient (r). Only ST models are therefore presented here.
   Structural time series (ST) models
   Intuitively, an ST model can be thought of as a regression model in which the explanatory variables are functions of time and the parameters are time-varying. For our models we have used the classical decomposition described by Harvey[16] in which the series is seen as the sum of trend, seasonal and irregular components. Fitting of ST models is a complex (but readily automated) procedure, full technical details of which have been described by Harvey[16]. For our ST models we incorporated only a weekly periodicity and not the annual periodicity indicated by the power spectra (cf, fig 2), as short-term forecasts will be dominated by the weekly periodicity.
   The "training" data — the first 1456 days (4 years) in the time series — were used to fit ST models with a weekly periodicity. These models were then used to forecast arrivals at forecast horizons l ranging from 1 to 7 days ahead. More precisely, we used the initial 1456 data points to fit our models and then used these models to predict the number of arrivals for the lth day ahead; we then shifted ahead into the remaining data by l data points and used the next 1456 data points to fit a new ST model and again calculated the lth day ahead prediction. This was repeated until we had shifted through the remaining 370 days of data. The set of lth day ahead predictions were then compared with the actual arrivals for the corresponding days in the "unseen" data. To indicate the quality of forecasts from these models, we calculated the mean of the bias of the predictions (which indicates if our models tend to overestimate or underestimate), the RMSE and the r value for each forecast horizon l. For each prediction made by the models the corresponding 95% confidence interval was also calculated. For each forecast horizon we computed the mean width of the 95% confidence intervals for the corresponding set of predictions. Finally we constructed scatterplots to show visually the quality of the forecast for the 1-day ahead predictions.

RESULTS

   Of the "training" data, 101 811 (27.6%) patient arrivals were classified as ambulance arrivals and 267 375 (72.4%) as walk-in arrivals. Of the "unseen" data, 27 403 (26.7%) were classified as ambulance arrivals and 75 315 (73.3%) as walk-in arrivals. Tables 1 and 2 show the quality of forecast metrics and the mean 95% confidence interval width for the 1–7-day ahead walk-in and ambulance arrival predictions, respectively. Figure 3 shows the scatterplots of the observed "unseen" data against the 1-day ahead walk-in (left) and ambulance (right) arrival model predictions.

Table 1 Quality of forecast metrics for the walk-in arrival model predictions
l Mean bias RMSE r 95% CI width
1 0.6257 18.0185 0.6205 ±34.3215
2 0.5042 17.7694 0.6095 ±35.2163
3 0.9841 20.8653 0.5426 ±36.0673
4 1.4213 19.2425 0.5264 ±36.9521
5 1.6864 20.6583 0.6114 ±37.9560
6 1.4356 21.0688 0.5534 ±38.4447
7 -1.1342 19.5209 0.2608 ±55.3970
  Table 2 Quality of forecast metrics for the ambulance arrival model predictions
l Mean bias RMSE r 95% CI width
1 0.2944 9.0364 0.2951 ±18.3133
2 -0.5935 9.0146 0.2030 ±18.3456
3 -0.0380 9.2714 0.1873 ±18.4050
4 -0.8125 8.7768 0.2318 ±18.4465
5 0.2909 8.8092 0.3478 ±18.4977
6 -0.0374 10.1434 -0.0374 ±18.5300
7 1.0104 10.1481 -0.04438 ±18.6486
   CI, confidence interval;
   r, Pearson’s product-moment correlation coefficient;
   RMSE, root mean square error.

DISCUSSION

   As already observed, it is clear from the power spectra of the walk-in and ambulance arrivals (see fig 2) that they have very different characteristics; this may be because walk-in arrivals (the majority of which will have minor illnesses/injuries) have more of a choice when deciding the most convenient time to go into A&E, while ambulance arrivals will tend to call an ambulance as and when needed (owing to the more serious nature of their illness/injury). This observation is consistent with the findings of other studies[16-17].

Figure 3 Scatterplots comparing the 1-day ahead structural time series (ST) model predictions for walk-in (A) and ambulance (B) arrivals with the "unseen" observed patient arrivals.

   From tables 1 and 2 it is apparent that the ST model forecasts for the walk-in arrivals show mostly a small positive mean bias while the forecasts for the ambulance arrivals show no trend in the bias. Table 1 and the scatterplot on the left in fig 3 show that the ST model of walk-in arrivals performs well, with our 1-day ahead predictions showing good correlation with the observed "unseen" data (r=0.6205). As expected, when predicting further ahead, the quality of forecast deteriorates; however, for up to 6 days ahead this deterioration is slow, with a trend towards the mean 95% confidence interval widths increasing slightly and r value slowly decreasing. For a 7-day forecast horizon we can see that the r value decreases sharply and the mean confidence interval idth increases steeply. This may be related to the strong 7-day seasonality in the walk-in ST model. From table 2 we see that the quality of the ST ambulance model predictions are not as good, with our 1-day ahead predictions showing poor correlation with the observed "unseen" data (r=0.2951) while the 6- and 7-day ahead forecasts show virtually no correlation to the actual arrivals (r=20.0374 and r=20.0443, respectively). This is reinforced by the 1-day ahead scatterplot shown on the right in fig 3. These results show that we can characterise walk-in arrivals effectively and that our 1–6-day ahead forecasts have good predictive power. However, it can be seen that we had less success with our ambulance arrival models. This may be because the ambulance arrivals do not exhibit any strong periodicities or other regularity. Thus, the ambulance arrival streams might not be suited to this method of time series analysis.
   We have also investigated characterising ambulance arrivals by a classical Poisson process and also a non-homogeneous Poisson process[18-19], but our "training" data failed both the corresponding goodness of fit tests.
   Despite being only able to characterise and forecast walk-in arrivals, these model forecasts will still be of value to hospital managers at our case study hospital as walk-in arrivals account for the majority of arrivals into the A&E department. These methods may also be useful in characterising and forecasting daily arrivals into other A&E departments as well as other forms of hospital arrivals such as emergency hospital admissions[11] and non-emergency hospital department arrivals. However, these lines of enquiry require further investigation.
   Other future research in this area may include further characterising the ambulance arrivals using other types of stochastic processes. Better models for walk-in arrivals may also be fitted as more data become available; this could involve fitting a multi-seasonal structural time series model which can incorporate both a weekly and an annual seasonality[20].
   Acknowledgements: The authors are grateful for the help and advice of many members of staff at the case study hospital and associated institutions.
   Competing interests: None.
   Ethics approval: Ethical approval for access to pseudonymised patient records was granted by the Harrow local research ethics committee (Ref 04/Q0405/72).

REFERENCES

  1. Healthcare Commission. National standards, local action: health and social care standards and planning framework 2005/06–2007/08. Technical report. London: Healthcare Commission, 2004.
  2. Department of Health. Quarterly monitoring of key standards and targets: accident and emergency, England (QMAE). London: Department of Health, 2006.
  3. Connelly LG, Bair AE. Discrete event simulation of emergency department activity: a platform for system-level operations research. Acad Emerg Med 2004; 11: 1177–85.
  4. Centeno MA, Giachetti R, Linn R, et al. A simulation-ILP based tool for scheduling ER staff. Proceedings of the 2003 Winter Simulation Conference 2003: 1930–8.
  5. Coats TJ, Michalis S. Mathematical modelling of patient flow through an accident and emergency department. Emerg Med J 2001; 18: 190–2.
  6. Rossetti MD, Trzcinski GF, Syverud SA. Emergency department simulation and determination of optimal attending physician staffing schedules. Proceedings of the 1999 Winter Simulation Conference 1999:1532–40.
  7. Miro O, Sanchez M, Espinosa G, et al. Analysis of patient flow in the emergency department and the effect of an extensive reorganisation. Emerg Med J 2003; 20: 143–8.
  8. Eldabi T, Young T, Picton C. Simulation modelling in healthcare: reviewing legacies and investigating futures. J Operational Res Socy 2007;58:262–70.
  9. Cooke M, Fisher J, Dale J, et al. Reducing attendances and waits in emergency departments: a systematic review of present innovations. Technical report. Report to the National Co-ordinating Centre for NHS Service Delivery and Organisation R & D (NCCSDO), 2005.
  10. Channouf N, L’Ecuyer P, Ingolfsson A, et al. The application of forecasting techniques to modeling emergency medical system calls in Calgary, Alberta. Health Care Manage Sci 2007; 10: 25–45.
  11. Jones SA, Joy MP, Pearson J. Forecasting demand of emergency care. Health Care Manage Sci 2002;5:297–305.
  12. Tandberg D, Qualls C. Time series forecasts of emergency department patient volume, length of stay, and acuity. Ann Emerg Med 1994;23:299–306.
  13. R Development Core Team. R: a language and environment for statistical computing. Vienna: R Foundation for Statistical Computing, 2007. http://www.R-project.org.
  14. Harvey AC. Time series models. Deddington: Philip Allan, 1981.
  15. Box GEP, Jenkins GM, Reinsel GC. Time series analysis: forecasting and control. 3rd ed. New Jersey: Prentice Hall, 1994.
  16. Harvey AC. Forecasting, structural time series models and the Kalman filter. Cambridge: Cambridge University Press, 1989.
  17. Codrington-Virtue A. Simulating accident and emergency services with a generic process. Nosokinetics Newsletter. Issue 26, December 2005.
  18. Kuhl ME, Wilson JR, Johnson MA. Estimating and simulating Poisson processes having trends or multiple periodicities. IIE Trans 1997; 29: 201–11.
  19. Massey WA, Parker GA, Whitt W. Estimating the parameters of a nonhomogeneous Poisson process with linear rate. Telecommun Syst 1996; 5: 361–88.
  20. Gould PG, Koehler AB, Vahid-Araghi F, et al. Forecasting time-series with multiple seasonal patterns. Eur J Operational Res 2008; 191: 205–20.