Прогнозирование прибытия пациентов в отделение травматологической и неотложной помощи

S W M Au-Yeung, U Harder, E J McCoy, W J Knottenbelt

Перевод с английского: Казакова О. С.

Источник: Emerg Med J 2009 26: 241-244. http://emj.bmj.com/content/26/4/241.full.pdf

АННОТАЦИЯ

    Цели: Охарактеризовать и спрогнозировать ежедневное прибытие пациентов в отделение травматологической и неотложной помощи (ТиНП) на основе предыдущих данных.
    Методы: Прибытия пациентов в отделение травматологической и неотложной помощи в период с 1 апреля 2002 года по 31 марта 2007, используемые в нашем исследовании, были отнесены к одному из двух потоков (пришедшие на приём и доставленные машиной скорой помощи) по способу прибытия и затем сгруппированы по дням. Используя данные первых 4-х лет о прибытиях пациентов как «обучающий» набор, структурная модель временных рядов (ST) была приспособлена для характеристики каждого потока прибытия пациентов. Эти модели были использованы для прогнозирования числа пациентов, пришедших на приём и доставленных на машине скорой помощи, на 1 – 7 дней вперед и результаты прогноза сравнены с наблюдаемым числом прибывших пациентов, полученными из «тестовой» выборки (оставшийся 1 год).
    Результаты: Ряд, описывающий число пациентов, пришедших на приём, имеет сильную 7-дневную сезонность; ряд, описывающий число пациентов, доставленных машиной скорой помощи, показывает отчетливую, но более слабую 7-дневную сезонность. Модель прогнозирования числа пациентов, пришедших на приём, показала приемлемую степень прогнозирования (r=0.6205). Однако, число пациентов, доставленных машиной скорой помощи, охарактеризировать было труднее (r=0.2951).
    Выводы: Два отдельных потока прибытия пациентов показывают различные статистические особенности и требуют применения различных моделей временных рядов. Точно охарактеризовать и спрогнозировать удалось только число пациентов, пришедших на приём, однако эта модель прогнозирования все-таки поможет руководителям больниц лучше использовать имеющиеся ресурсы и прогнозировать периоды высокого спроса, так как пациенты, пришедшие на приём, составляют большинство прибывших в отделения травматологической и неотложной помощи.

    Отделы травматологической и неотложной помощи (ТиНП) оказываются во все более затруднительном состоянии, так как должны обслуживать увеличивающееся число пациентов благополучно и быстро. Об этом свидетельствует цель правительства: 98% пациентов должны проводить 4 часа или менее с момента прибытия до приёма, перемещения или выписки, в связи с увеличением числа посещений отделений ТиНП и медицинских центров в Англии (с 16,5 млн. посещений в 2003 году до 18,9 млн. в 2007). Одновременно с этим в 2003 – 2006 годах семь больниц сообщили, что один или несколько отделов травматологической и неотложной помощи закрылись или были сокращены, и всего один отдел ТиНП был открыт. Важно понять и охарактеризовать природу прибытия пациентов, чтобы иметь возможность заранее запланировать эффективное штатное расписание и потребность в ресурсах для остальных открытых отделов ТиНП.
    Существует много исследований, описывающих моделирование работы отделений ТиНП (или отделений неотложной помощи в других странах кроме Великобритании), в которых для характеристики процесса прибытия пациентов принято либо распределение Пуассона, либо используются исторические данные.
    Чтобы текущие и будущие процессы моделирования и модели ТиНП были эффективными при обеспечении улучшений, они должны быть согласованы с реальной рабочей нагрузкой отделений. Использование распределения Пуассона или репродукции исторических данных, гораздо упрощает оценивание, поскольку в первом случае известно, что спрос на неотложную медицинскую помощь представляет собой сезонную модель с более высоким числом обслуживаний в летние месяцы и более высокой потребностью в бригадах интенсивной терапии в зимние месяцы; в последнем случае не составляются долгосрочные тенденции.
    В других исследованиях были попытки описать и спрогнозировать острые периоды прибытия пациентов в больницу, используя различные модели временных рядов, включая авторегрессионную модель (AR), скользящее среднее (МА) и авторегрессионное интегрированное скользящее среднее (ARIMA). Однако, эти исследования рассматривают только случаи неотложной госпитализации, прибытия машины скорой помощи или общее число пришедших пациентов без разграничения между различными типами прибытия пациентов.
    В этой статье представляется новый подход к прогнозированию числа пациентов отделения ТиНП с помощью спектрального анализа плотности и структурной модели временных рядов. Структурные модели временных рядов наиболее подходят для наборов данных, таких, как потоки прибытия пациентов в отделения ТиНП, которые показывают сезонность и не являются стационарными (то есть статистические свойства данных, такие как среднее, дисперсия и автокорреляционная структура изменяются с течением времени). Кроме того, в отличие от предыдущих работ, мы используем отдельные модели временных рядов для характеристики и прогнозирования числа пациентов, пришедших на приём и доставленных машиной скорой помощи, в отличие от моделирования либо общего числа пациентов, либо только числа пациентов, которых привозит машина скорой помощи.
    Это исследование основывается на данных о прибытии пациентов за 5 лет, предоставленных отделением травматологической и неотложной помощи больницы North London, которая обслуживает более чем 100000 посетителей ежегодно и число приёмов увеличивается приблизительно на 25%. Наши задачи
    1) использовать «обучающие» данные для характеристики каждого из потоков прибытия пациентов, выполнив спектральный анализ данных и построив соответствующую модель временных рядов,
    2) для проверки прогнозирующей способности (с точки зрения прогнозирования ежедневного числа пациентов, пришедших на приём и доставленных машиной скорой помощи) модели временных рядов для каждого потока прибытия пациентов используются «тестовые» данные.

МЕТОДЫ

    В нашем исследовании были изучены все пациенты, прибывшие в отделение ТиНП в период с 1 апреля 2002 года по 31 марта 2007. Пациенты были классифицированы либо как прибывшие на машине скорой помощи (если электронная запись указывает, что пациент прибыл на санитарной машине), либо прибывшие на приём (все другие виды прибытия пациентов). Затем эти наборы данных были сгруппированы, чтобы получить отдельные временные ряды числа прибывших пациентов на машине скорой помощи и на прием в день. Эти два временных ряда ежедневного прибытия пациентов были дополнительно разбиты на «обучающие» данные, состоящие из первых 4-х лет (1456 дней) и «тестовые» данные, состоящих из остальных 370 дней, которые используются для определения точности наших моделей прогнозирования. Все модели временных рядов в данном исследовании были созданы и установлены с использованием статистического пакета программ R; R сценарии, используемые в этом исследовании, могут быть найдены на http://www.doc.ic.ac.uk/,swa02/ST.txt.
    Предварительный анализ данных
    Графики «обучающих» данных числа пациентов прибывших на приём и на машине скорой помощи за день представлены на рисунке 1. Чтобы определить периодичность, к этим временным рядам был применен анализ спектральной плотности, который описывает, как мощность временного ряда распространяется по частоте. Результаты этого анализа приведены на рисунке 2. Временной ряд, который описывает самостоятельно прибывших пациентов, показывает ярко выраженные пики в спектре мощности соответствующие еженедельному (7 дней) периодичному поведению данных. Начальный большой пик на низких частотах показывает ежегодную периодичность, а более низкие пики (2 и 3) соответствуют гармонике главной 7-дневной частоты. Временной ряд, который описывает число пациентов, прибывших на машине скорой помощи показывает отдельную, но более слабую 7-ми дневную периодичность, а так же годовую периодичность. Различные спектральные особенности подчеркивают необходимость использования различных моделей временных рядов для каждого типа прибытия пациентов.


Рисунок 1. Временные ряды, которые описывают число пациентов, пришедших на прием (А), и число пациентов, прибывших на машине скорой помощи (В)

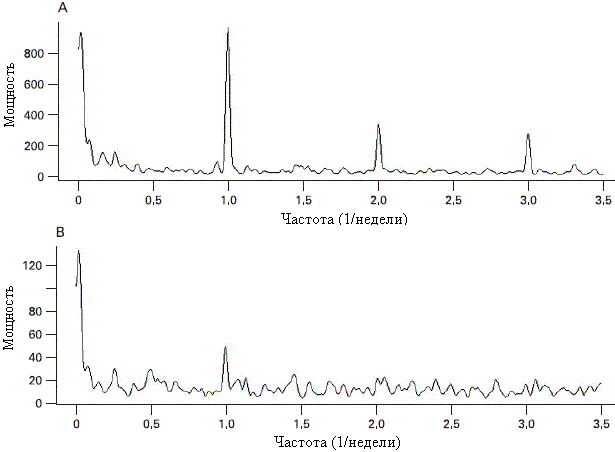Рисунок 2. Спектры мощности временных рядов, которые описывают число пациентов, при-шедших на прием (А), и число пациентов, прибывших на машине скорой помощи (В)

    Были установлены два типа моделей временных рядов: AR модель и ST модель. Мы рассмотрели AR модели, так как она часто применяются для показа регулярности временных рядов. Однако ST модель больше подходит для наших потребностей, поскольку они
    1) не требуют предварительной обработки данных для удовлетворения предположения ста-ционарности (в отличие от модели AR);
    2) позволяют явно включать сезонные факторы и местные линейные тенденции;
    3) работают лучше для обоих случаев с точки зрения среднеквадратичной ошибки (СКО) и коэффициента корреляции Пирсона.
    Поэтому здесь представлены только ST модели.
    Структурные модели временных рядов (ST)     Интуитивно понятно, что модель ST можно рассматривать как модель регрессии, в которой независимые переменные – функции времени и параметры – изменение времени. Для нашей модели мы использовали классическое разложение, описанное Harvey, в котором ряд рассматривается как сумма тренда, сезонных и нерегулярных компонент. Установка ST модели сложная процедура, все технические детали которой были описаны Harvey. Для нашей ST модели мы включили только еженедельную периодичность, а не ежегодную, показанную спектральной частотой (см. рисунок 2), поскольку в краткосрочных прогнозах будут доминировать еженедельные периодичности.
    Обучающие данные – первые 1456 дней (4 года) временного ряда – были использованы для установления еженедельной периодичности структурной модели временных рядов. Эти модели затем были использованы для прогнозирования прибытия пациентов на период от 1 до 7 дней вперед. Точнее, мы использовали первоначальные 1456 точек данных, чтобы подстроить нашу модель, а затем использовали модель для прогнозирования числа пациентов на 1 день вперед; затем мы сместили вперед на 1 точку остальные данные и использовали следующие 1456 точек для определения новой ST модели и снова рассчитали прогноз на 1 день вперед. Это было повторено, пока мы не сдвинулись на 370 дней. Набор спрогнозированных на 1 день вперед значений был сравнен с фактическими данными соответствующих дней тестового набора данных. Чтобы указать качество прогнозов этих моделей мы рассчитали среднее смещение прогнозов (которое указывает, имеют ли наши модели тенденцию оценивать слишком высоко или недооценивать), СКО и значение r для каждого прогноза. Для каждого прогноза, сделанного с помощью моделей так же был вычислен соответствующий 95%-ный доверительный интервал. Для каждого периода прогнозирования мы вычислили среднюю ширину 95%-ных доверительных интервалов. Наконец мы построили диаграммы рассеивания, чтобы показать визуально качество прогноза на 1 день вперед.

РЕЗУЛЬТАТЫ

    Из обучающих данных 101811 (27,6%) пациентов были классифицированы как прибывшие на машине скорой помощи и 267375 (72,4%) как пришедшие на приём. Из тестового набора данных 27403 (26,7%) пациентов были классифицированы как прибывшие на машине скорой помощи и 75315 (73,3%) как пришедшие на приём. В таблицах 1 и 2 представлены показатели качества прогнозов и средняя ширина 95% доверительного интервала для прогнозов на 1 – 7 дней вперед. На рисунке 3 представлены диаграммы рассеивания тестовых данных для прогноза на 1 день вперед.

Таблица 1 Показатели качества прогноза для модели прогнозирования числа пациентов, прибывших на приём
l Среднее смещение СКО r 95% CI ширина
1 0.6257 18.0185 0.6205 ±34.3215
2 0.5042 17.7694 0.6095 ±35.2163
3 0.9841 20.8653 0.5426 ±36.0673
4 1.4213 19.2425 0.5264 ±36.9521
5 1.6864 20.6583 0.6114 ±37.9560
6 1.4356 21.0688 0.5534 ±38.4447
7 -1.1342 19.5209 0.2608 ±55.3970
  Таблица 2 Показатели качества прогноза для модели прогнозирования числа пациентов, прибывших на машине скорой помощи
l Среднее смещение СКО r 95% CI ширина
1 0.2944 9.0364 0.2951 ±18.3133
2 -0.5935 9.0146 0.2030 ±18.3456
3 -0.0380 9.2714 0.1873 ±18.4050
4 -0.8125 8.7768 0.2318 ±18.4465
5 0.2909 8.8092 0.3478 ±18.4977
6 -0.0374 10.1434 -0.0374 ±18.5300
7 1.0104 10.1481 -0.04438 ±18.6486
    CI – доверительный интервал;
    r – коэффициент корреляции Пирсона;
    СКО – среднеквадратичная ошибка.

ОБСУЖДЕНИЕ

    Как уже отмечалось, из спектров мощности (см. рисунок 2) видно, что прибытия пациентов санитарной машиной и на приём имеют различные характеристики. Это может быть из-за того, что у пациентов, которые приходят в больницу на прием (большинство из них имеет незначительные болезни/травмы) есть возможность выбрать более удобное время, чтобы прийти в отделение травматологической и неотложной помощи, а прибытие пациентов на машине скорой помощи имеет тенденцию вызовов скорой (из-за более серозного характера болезней и травм). Это наблюдение согласуется и с результатами других исследований.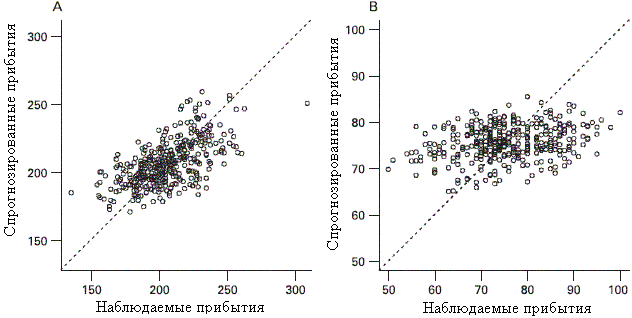

Рисунок 3. Диаграммы рассеяния для прогноза на 1-день вперед с помощью модели структурных временных рядов числа пациентов, при-шедших на прием (А), и числа пациентов, прибывших на машине скорой помощи (В)

    Из таблиц 1 и 2 видно, что ST модель прогнозирования числа пациентов, которые придут на прием показывает небольшое среднее смещение, в то время как прогнозирование числа пациентов, прибывших на машине скорой помощи, не проявляет тенденцию смещения. Таблица 1 и левый график рассеивания на рисунке 3 показывают, что ST модель прогнозирования числа пациентов, которые придут на прием работает хорошо, прогноз на 1 день вперед показывает хорошую корреляцию с наблюдаемыми тестовыми данными (r=0.6205). Как ожидалось, при прогнозировании на больший период, качество прогнозов ухудшается; однако, на срок до 6 дней это ухудшение является небольшим, с тенденцией к небольшому увеличению ширины 95% доверительного интервала и убыванию значения r. Для прогноза на период 7 дней мы видим, что значение r резко убывает и доверительный интервал резко увеличивается. Это может быть связано с сильной 7-дневной сезонностью ST модели прогнозирования числа пациентов, пришедших на приём. Из таблицы 2 видно, что качество прогнозов числа пациентов, доставленных на машине скорой помощи не столь хорошо, прогноз на 1 день вперед показывает плохую корреляцию с наблюдаемыми тестовыми данными (r=0.2951), а прогнозы на 6 и 7 дней вперед показывают плохую корреляцию с фактическими данными (r=20.0374 и r=20.0443 соответственно). Это усиливается графиком рассеивания на 1 день вперед, представленным справа на рисунке 3. Эти результаты показывают, что мы можем эффективно характеризовать прибытия пациентов на прием и наши прогнозы на 1 – 6 дней вперед имеют хорошую прогнозирующую способность. Однако можно заметить, что модель прибытия пациентов на машине скорой помощи менее удачна. Возможно это из-за того, что прибытия машины скорой помощи не проявляют какую-либо сильную периодичность или другую закономерность. Таким образом, применение этого метода анализа временных рядов не может быть применено к прибытию пациентов на машине скорой помощи.     Мы так же исследовали характеристики прибытия пациентов на машине скорой помощи классическим процессом Пуассона, а так же неоднородным пуассоновским процессом, но наши обучающие данные не соответствуют критериям согласия.
    Несмотря на то, что можно охарактеризовать и спрогнозировать только число пациентов, которые придут на приём, эта модель прогнозирования имеет ценность для руководителей больниц, так как пациенты, пришедшие на приём, составляют большинство прибывших в отделения травматологической и неотложной помощи. Эти методы так же могут быть полезными при характеристике и прогнозировании ежедневного прибытия пациентов в другие отделения травматологической и неотложной помощи. Однако, эти направления исследования требуют дальнейших разработок.
    Будущие исследования в этой области могут включать дальнейшую характеристику прибытия пациентов на машине скорой медицинской помощи, используя другие типы вероятностных процессов. Лучшие модели для определения числа пациентов, пришедших на приём, могут так же быть модифицированы, так как появятся дополнительные данные; можно добавить установку структурной модели временных рядов, которая будет включать и еженедельную и ежегодную сезонность.

Литература

  1. Healthcare Commission. National standards, local action: health and social care standards and planning framework 2005/06–2007/08. Technical report. London: Healthcare Commission, 2004.
  2. Department of Health. Quarterly monitoring of key standards and targets: accident and emergency, England (QMAE). London: Department of Health, 2006.
  3. Connelly LG, Bair AE. Discrete event simulation of emergency department activity: a platform for system-level operations research. Acad Emerg Med 2004; 11: 1177–85.
  4. Centeno MA, Giachetti R, Linn R, et al. A simulation-ILP based tool for scheduling ER staff. Proceedings of the 2003 Winter Simulation Conference 2003: 1930–8.
  5. Coats TJ, Michalis S. Mathematical modelling of patient flow through an accident and emergency department. Emerg Med J 2001; 18: 190–2.
  6. Rossetti MD, Trzcinski GF, Syverud SA. Emergency department simulation and determination of optimal attending physician staffing schedules. Proceedings of the 1999 Winter Simulation Conference 1999:1532–40.
  7. Miro O, Sanchez M, Espinosa G, et al. Analysis of patient flow in the emergency department and the effect of an extensive reorganisation. Emerg Med J 2003; 20: 143–8.
  8. Eldabi T, Young T, Picton C. Simulation modelling in healthcare: reviewing legacies and investigating futures. J Operational Res Socy 2007;58:262–70.
  9. Cooke M, Fisher J, Dale J, et al. Reducing attendances and waits in emergency departments: a systematic review of present innovations. Technical report. Report to the National Co-ordinating Centre for NHS Service Delivery and Organisation R & D (NCCSDO), 2005.
  10. Channouf N, L’Ecuyer P, Ingolfsson A, et al. The application of forecasting techniques to modeling emergency medical system calls in Calgary, Alberta. Health Care Manage Sci 2007; 10: 25–45.
  11. Jones SA, Joy MP, Pearson J. Forecasting demand of emergency care. Health Care Manage Sci 2002;5:297–305.
  12. Tandberg D, Qualls C. Time series forecasts of emergency department patient volume, length of stay, and acuity. Ann Emerg Med 1994;23:299–306.
  13. R Development Core Team. R: a language and environment for statistical computing. Vienna: R Foundation for Statistical Computing, 2007. http://www.R-project.org.
  14. Harvey AC. Time series models. Deddington: Philip Allan, 1981.
  15. Box GEP, Jenkins GM, Reinsel GC. Time series analysis: forecasting and control. 3rd ed. New Jersey: Prentice Hall, 1994.
  16. Harvey AC. Forecasting, structural time series models and the Kalman filter. Cambridge: Cambridge University Press, 1989.
  17. Codrington-Virtue A. Simulating accident and emergency services with a generic process. Nosokinetics Newsletter. Issue 26, December 2005.
  18. Kuhl ME, Wilson JR, Johnson MA. Estimating and simulating Poisson processes having trends or multiple periodicities. IIE Trans 1997; 29: 201–11.
  19. Massey WA, Parker GA, Whitt W. Estimating the parameters of a nonhomogeneous Poisson process with linear rate. Telecommun Syst 1996; 5: 361–88.
  20. Gould PG, Koehler AB, Vahid-Araghi F, et al. Forecasting time-series with multiple seasonal patterns. Eur J Operational Res 2008; 191: 205–20.