Расчет неопределенности модели прогнозирования чрезвычайных ситуаций в городской среде

Tonio Fincke, Jochen Schiewe, and Karl-Peter Traub

Перевод: Казакова О. С.

Источник: http://www.isprs.org/proceedings/XXXVIII/2-W11/Fincke_Schiewe_Traub.pdf

Ключевые слова: факторы неопределенности, спасательные службы, городская среда, модель прогнозирования

АННОТАЦИЯ

   Хотя неопределенности проявляются почти в каждом процессе анализа или моделирования, она часто не рассматриваются или не описываются в явном виде. Особенно в сложных моделях они могут стать очень большими. Пренебрежение их описанием может привести к необоснованной уверенности в результатах. В этой статье представлен план разработки комплексной модели, в которой явно описано возникновение и распространение неопределенности данных. Для этой модели мы исследуем связь между социально-демографическими условиями и количеством чрезвычайных ситуаций в городских районах. Далее мы дадим оценку будущему развитию социально-демографических условий. Эти результаты послужат основой для прогнозирования чрезвычайных ситуаций в определенном районе. Мы выявим возможные источники неопределенности и представим первые идеи для их решения. Нашей целью является сформулировать неопределенность результата модели.

1 ВВЕДЕНИЕ

   Неопределенность данных происходит на любом шаге обработки данных. Она может появляться или увеличиваться за счет измерений, сбора, агрегации, преобразования, передачи, распространения, моделирования или старения данных. В сложных моделях данные собираются из различных источников, перестроенных, чтобы соответствовать нынешним потребностям, обрабатываются в соответствии с типовыми предположениями, и распространяются, служа входными данными для процессов в рамках модели. Соответственно, это так же сохраняет неопределенности данных (MacEachren, 1992, и др. MacEachren., 2005). Поскольку неопределенность, как правило, увеличивается при обработке данных, полезность данных, полученных в рамках такой модели, может быть утверждена, только когда учитывается их неопределенность. Заявления о неопределенности могут изменить решение о том, как действовать, с какими данными. Таким образом, неопределенность может изменить конечный результат.
   Неопределенность возникает, например, в процессе моделирования взаимозависимостей между социально-демографическими показателями и инфраструктурой. Легко увидеть, что эти два параметра влияют друг на друга. Средства обеспечения специализированных услуг направлены на население. Они должны обслуживать либо определенное число людей, либо быть доступными в течение заданного времени. Инфраструктура услуг может влиять на конкретные потребности и характеристики населения вокруг объекта. С другой стороны, инфраструктурное оборудование могло бы привлечь или оттолкнуть людей и, следовательно, оказывает влияние на население и его характеристики.
   Конкретным примером объекта инфраструктуры является служба скорой медицинской помощи в городе Гамбург. В Гамбурге машины скорой помощи расположены на спасательных станциях, которые распределены по городу. Если произойдет чрезвычайная ситуация, то «штаб-квартира» скорой направит машину скорой помощи к месту аварии. В большинстве случаев, чрезвычайная ситуация будет обслуживаться машиной скорой помощи из станций, которые находятся ближе всего к инциденту. Однако, в некоторых случаях, все машины скорой помощи с одной станции могут быть заняты, и тогда должна быть направлена машина из другой станции. Также машина скорой помощи может пересекать область, которую обычно обслуживают машины из других станций и обслуживать вызов. Это происходит, например, когда санитарная машина находится на обратном пути из больницы.
   В этой статье мы покажем план комплексной модели городских процессов. Явно рассмотрим неопределенности. Мы хотим создать модель, которая может служить для прогнозирования чрезвычайных ситуаций в городе Гамбург в будущем. Эта модель будет основана на взаимосвязи между социально-демографическими характеристиками городских округов и количеством аварий, которые происходят в них. Районы в Гамбурге различаются по своей социально-демографической форме. Работники пожарной охраны отметили, что они могут наблюдать за изменением объемов и видов инцидентов относительно социально-демографической параметров района.
   Далее мы оценим будущие результаты социально-демографических характеристик и используем эти оценки в качестве основы для прогнозирования будущего количество чрезвычайных ситуаций. В этой работе неточная информация неоднократно используется для расчета, оценки или прогнозирования данных. Результаты в свою очередь так же будут неточными. Мы хотим рассмотреть несколько методов, моделирующих эту неопределенность, применить и сравнить их. Мы хотим разобраться в полезности существующих подходов к рассмотрению неопределенности и, возможно, обнаружить потенциал для новых подходов.
   В разделе 2 мы представим и обсудим соответствующие работы. Перед тем как мы объясним наш подход более подробно в разделе 4, в разделе 3 мы представим набор данных, которые будем использовать. В разделе 4 мы также явно обратимся к рассмотрению неопределенности. Закончим взглядом на возможные будущие работы в разделе 5.

2 ПРЕДЫДУЩАЯ РАБОТА

   В начале десятилетия было создано отображение «карты» здоровья для города Гамбург. Расчет цены операций был выполнен по данным о дорогах и местах спасательной станции. Таким образом, было исследовано, какие части города могут быть достигнуты в течение определенного времени. Позже было посчитано фактическое число чрезвычайных ситуаций, происходящих в этих областях. Это учитывается при предложении переназначения районов или станций скорой помощи или даже перемещения станций.
   Результаты «карты» здоровья показали, что 53,6% городской территории может быть достигнуто в течение пяти минут машинами скорой помощи. В этой области происходит 78,3% инцидентов. На основании «карты» здоровья предложено перемещение станций, которое позволило охватить 55,3% территории и 86,6% всех инцидентов, которые могут быть достигнуты скорой помощью в течение 5 минут (Traub, 2003, Traub, 2004, Albers, 2001, Henning, 2001). Результаты этой работы представлены на рисунках 1 и 2.


Рисунок 1: Фактическое распределение спасательных станций
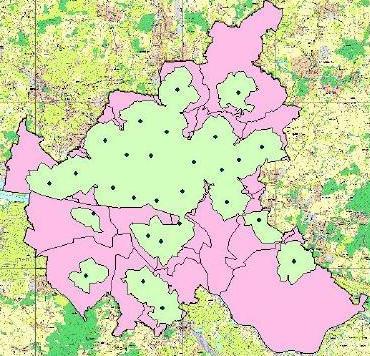Рисунок 2: Оптимизированное распределение спасательных станций

   Рисунок 1 показывает распределение спасательных станций до оптимизации, рисунок 2 показывает распределение после оптимизации. На обоих изображений, точки представляют спасательных станций, меньшие области представляют собой части, которые могут быть достигнуты в течение 5 минут от спасательной станции, и большие площади показывают области, которые обычно обслуживаются соответствующими спасательными станциями.
   Krisp и Karasova рассмотрели взаимосвязь между плотностью населения и чрезвычайными происшествиями (Krisp и Karasova, 2005). В то время они обнаружили, что корреляция была значительной, но также стало ясно, что должно быть больше факторов, определяющих возникновение чрезвычайных ситуаций. В более поздних работах, были рассмотрены на только плотность населения, а также изменение местоположения людей в течение дня или ночи (Ahola и др.., 2007, Krisp, 2008), временное распределение инцидентов (Spatenkova и др.., 2007) или возраст больных. Результаты показали, что чрезвычайные ситуации являются наиболее частыми в районах, где много пожилых людей. Кроме того, подобные инциденты варьируется в зависимости от распределения по возрасту (Spatenkova и Krisp, 2007).

3 НАБОР ИСПОЛЬЗУЕМЫХ ДАННЫХ

   В нашей работе мы будем использовать два различных набора данных: один о чрезвычайных ситуациях и один о социально-демографических данных.
   TДанные о чрезвычайных ситуациях состоят из звонков, которые поступили в аварийный штаб Гамбурга в 2004 – 2008 годах. Каждая чрезвычайная ситуация описывается следующими параметрами:
   Машина скорой помощи обозначается составным идентификатором (ID), который состоит из идентификатора спасательной станции санитарной машины и уникального символа идентификации (например, санитарная машина 11A была бы санитарной машиной спасательной станции 11).
   Из-за ограничений данных, место чрезвычайной ситуации не обозначается географическими координатами или номером дома, а только улицей. Это приводит к необычным ситуациям, когда большинство мест чрезвычайных ситуаций включены в качестве функции линии. Кроме того, некоторые места чрезвычайных ситуаций даже не кодируются улицей, а задаются известными зданиями или другими объектами, такими как городские железнодорожные станции, врачебные кабинеты, школы, гостиницы, парки и другие.
   Другой набор данных содержит различные социально-демографические атрибуты городских районов Гамбурга за 1986 – 2007 года. Это общедоступные данные из статистического бюро Гамбурга и Шлезвиг-Гольштейна. Набор данных состоит из более ста переменных о населении, возрастном составе, доходах, занятости, преступлениях и миграции. Однако некоторые данные доступны только с, до или за определенные года.
   Кроме того, значения атрибутов сдвинуты во времени. Имели место изменения, касающиеся областей районов, а так же значений атрибутов. В 2008 году были созданы новые районы, забрав часть других районов. Один район был ликвидирован. Относительно тематических атрибутов ограничения могут измениться из года в год. Например, для значения безработицы молодых людей нет однозначной трактовки, в каком возрасте человека считают «молодым». Кроме того, некоторые данные, определяется расчетным путем. Например, последняя перепись населения в Германии была проведена в 1987. Таким образом, данные о численности населения не являются точно достоверными и иногда получают случайные сдвиги, когда реестр жителей очищаются от нескольких неисправных записей сразу.

4 СХЕМА НАШЕГО ПОДХОДА

   В этом разделе мы наметим наши планы относительно модели анализа связей между социально-демографическими факторами и количеством чрезвычайных ситуаций в пределах городских районов. Мы также расскажем, как планируем использовать эту модель для прогнозирования будущей чрезвычайных ситуаций. Тем не менее, мы обратим внимание на выявление, обработку и описание неопределенности в рамках анализа. Для реализации модели и описания неопределенности, мы планируем использовать Java и R.
   В качестве первого шага подготовим данные для анализа. Чтобы это сделать, необходимо обнаружить недостающие данные, дублирование данных и очевидно неправильные значения. Эти значения могут быть удалены или заменены интерполированными значениями, чтобы получить данные, которые свободны от возмущающих воздействий.
   Рассмотрение неопределенности в этой части анализа будет сложным, так как никакая априорная информация о наборах данных не доступна. Самым разумным решением в этом пункте будет рассмотреть точную информацию (или, по крайней мере, достаточно достоверную для наших целей).
   Следующим шагом будет вычисление общего количества чрезвычайных ситуаций в районе. Большинство чрезвычайных ситуаций кодируются улицей. Поскольку в большинстве случаев улица находится полностью в пределах одного района, большинство чрезвычайных ситуаций может быть однозначно отнесено к определенному району. Более непонятный случай, когда улица проходит через один или несколько районов. В таких случаях существует несколько вариантов. Пусть ci будет счетчиком чрезвычайных ситуаций в районе i, n – число районов, через которые проходит улица и p(i) – процент улицы, который проходит через район i. Возможные варианты обновления значения счетчика cinew показаны в уравнениях (1), (2), (3).
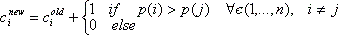(1)
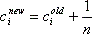(2)
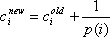(3)
Для того чтобы описать неопределенность, было бы целесообразно использовать три счетчика:    Очевидно, что имеет место уравнение (4).
c1 >= c2 >= c3 (4)
   Эти три значения счетчиков могут быть использованы для моделирования функция плотности вероятности. Полезность функции плотности вероятности для описания неопределенности доказана (Morgan и Henrion, 1990). Другая проблема возникает в связи с чрезвычайными ситуациями, положение которых задано не улицей, а другим местом. Назначение этим местам районов было бы слишком громоздким для выполнения, так как названия места часто появляются только один раз. Однако, поскольку для каждой чрезвычайной ситуации предоставляется информация о спасательной станции, которая обслужила чрезвычайную ситуацию, можно оценить в каком районе мог произойти инцидент. Нельзя исключать любой специфический район, так как машина скорой помощи могла обслуживать чрезвычайную ситуацию в этом районе по случайному стечению обстоятельств. Модели для определения района чрезвычайной ситуации могут учитывать:    c1, c2, и c3 могут быть соответственно увеличены.
   На следующем шаге мы хотим применить модель, в которой социально-демографические факторы служат для оценки общего числа чрезвычайных ситуаций в районе. Учитывая, что связь между социально-демографическими показателями и происходящими чрезвычайными ситуациями пока неизвестна, мы не можем сделать предварительное предположение о том, какие переменные использовать. Эту специальную задачу можно решить с помощью метода ступенчатой регрессии. Однако, если ступенчатую регрессию применять неосмотрительно, она может ввести многочисленную неопределенность. Слабые места и недостатки ступенчатой регрессии широко известны (Whittingham и др., 2006). Аналитики склонны рассматривать предложенную модель, как единственно лучшую модель, не зная или не предавая значения тому, что есть различные модели, которые выдают результаты аналогичного качества. Ступенчатая регрессия используется для решения проблемы о том, какие переменные включать в модель. В зависимости от последовательности, в которой переменные были включены или исключены из модели, будут произведены различные модели. Чтобы преодолеть эти недостатки, полезно рассмотреть не только лучшую, но и другие хорошо подобранные модели. Критерии отбора моделей были разработаны с целью справиться с возникающей неопределенностью (Akaike, 1974, Burnham и Anderson, 2002). Тем не менее, рассмотрение неопределенности на этом шаге также будет трудным.
   Дальнейшим аспектом будет продолжение социально-демографических факторов. Модели для продолжения демографических факторов (то есть, население) в основном состоят из четырех переменных: рождаемости, смертности, иммиграции и эмиграции. В то время как рождаемость и смертность можно оценить весьма достоверно, в основе иммиграция и эмиграция лежат влияния, которые очень трудно предвидеть. Что касается других социально-демографических факторов (например, развитие безработицы), мы планируем применить анализ временных рядов с целью получения оценки будущих выходных значений. Мы все еще должны узнать о функции моделей, которые соответствуют этой задачи прежде, чем мы выберем, как лучше всего описать неопределенность прогнозируемых значений. Мы ожидаем, что неопределенность возрастает с течением времени, таким образом, оценки для следующего года могут быть весьма точными, в то время как оценки для последующих годов будут более сомнительны.
   Прогнозируемые значения и модель регрессии будут служить, в конечном счете, для оценки будущих значений чрезвычайных ситуаций в районе. Так как неопределенность описывается и для значения модели, и для прогнозируемого значения, мы сможем оценить неопределенность результатов модели.
   Мы ожидаем, что на данном этапе модели неопределенность может быть очень большой. Это значит, что многие результаты представляются правдоподобными. Беспокоит то, что неопределенность в конечном счете становится настолько велика, что модель становится бесполезной. Большая неопределенность может оттолкнуть пользователя, и он примет решение не рассматривать оценки, которые являются весьма сомнительными. Для того, чтобы решить проблему широких границ неопределенности, мы могли бы исключить значения, которые весьма маловероятны из модели и рассмотреть только те значения, которые имеют значение вероятности, которое превосходит некоторый порог.

5 ВЫВОДЫ И БУДУЩАЯ РАБОТА

   Эта статья показывает, план проекта на стадии разработки. В нем рассматриваются различные аспекты, такие как    Мы изложили свой план реализации данного проекта и упомянули различные ситуации, когда мы ожидаем трудности в разработке модели и работе с данными и моделью неопределенности. Для некоторых из этих ситуаций мы сказали, как планируем преодолевать эти трудности, для других мы все еще разрабатывает адекватные решения. Нашим следующим шагом будет нахождение решений для оставшихся проблем и реализация модели. Эта работа оставляет пространство для некоторых улучшений и дополнительного анализа или моделирования.
   Более надежная модель может быть построена с помощью социально-демографических данных для территории, которая меньше чем районы. Кроме того, могут быть полезными более уточненные данные о возрастном распределении. Это позволит обеспечить уточнение параметров регрессии и, следовательно, уменьшит неопределенность в модели. Однако, когда административные области меньше, меньше улиц будет полностью содержаться в них и меньше чрезвычайных ситуаций можно будет задать однозначно.
   После того, как количество чрезвычайной ситуации для каждого района было спрогнозировано, оно может использоваться для оценки будущей загрузки работы станции. Часть этой задачи будет состоять из анализа, какой район обслуживается какой станцией на сколько процентов. Такая модель требует специального рассмотрения и описания ее неопределенности. Если некоторый порог чрезвычайных ситуаций для станции превышен, это может означать, что требуются новые машины скорой помощи или новые станции.
   Бывший наш план состоит в применении микро-моделирования, в котором служба скорой помощи будет имитироваться в течение одного года. Это может повторяться несколько раз для того чтобы осуществить моделирование Монте-Карло. Результаты такого моделирования могут быть использованы для описания неопределенности с помощью функции плотности вероятности. Мы упростили этот план из-за его сложности и недостающей информации о типичном движении санитарных машин. Однако, этот подход может быть частью будущей работы, так как это позволит рассмотреть различные аспекты, которые не включены в нашу текущую модель. Среди этих аспектов сезонные изменения и передвижение по городской территории с несколькими естественными барьерами, такими как река Эльба.
   Другие возможные направления будущей работы будут увеличивать число анализируемых данных, основанных на данных о изменении численности населения и изучение взаимосвязи между социально-демографическими факторами и временными атрибутами, или типами чрезвычайных ситуаций.

БЛАГОДАРНОСТЬ
   Авторы хотели бы поблагодарить пожарную Гамбурга за их любезное сотрудничество.

СПИСОК ЛИТЕРАТУРЫ
  1. Ahola, T., Virrantaus, K., Krisp, J. M. and Hunter, G. J., 2007. A spatio-temporal population model to support risk assessment and damage analysis for decision-making. International Journal of Geographical Information Science 21, pp. 935–953.
  2. Akaike, H., 1974. A new look at the statistical model identification. IEEE Transactions on Automatic Control 19, pp. 716–723.
  3. Albers, M., 2001. GIS-gest?utzte Untersuchung zur distanzabh angigen Optimierung der Einsatzgebiete der Hamburger Feuerwehr. Diploma thesis (not published), HafenCity University Hamburg, formerly Fachhochschule Hamburg, Hamburg.
  4. Burnham, K. P. and Anderson, D. R., 2002. Model Selection and Multi-Model Inference: A Practical Information-Theoretic Approach. Springer-Verlag, New York.
  5. Henning, M., 2001. Raumliche Analyse der Rettungswachen der Berufsfeuerwehr Hamburg mit Hilfe eines Geoinformationssystems. Diploma thesis (not published), HafenCity University Hamburg, formerly Fachhochschule Hamburg, Hamburg.
  6. Krisp, J. M., 2008. Geoinformation for Civil Protection - Tracking Mobile Phones as a Data Source. CivPro column of the month.
  7. Krisp, J. M. and Karasova, V., 2005. The relation between population density and fire / rescue service incidents in urban areas. In: Proceedings on the 10th Scandinavian Research Conference on Geographical Information Science (ScanGIS), pp. 237–246.
  8. MacEachren, A. M., 1992. Visualizing Uncertain Information. Cartographic Perspective (13), pp. 10–19.
  9. MacEachren, A., Robinson, A., Hopper, S., Gardner, S., Murray, R., Gahegan, M. and Hetzler, E., 2005. Visualizing Geospatial Information Uncertainty: What We Know and What We Need to Know. Cartography and Geographic Information Science 32(3), pp. 139–160.
  10. Morgan, M. G. and Henrion, M., 1990. Uncertainty: A Guide to dealing with uncertainty in quantitative risk and policy analysis. Cambridge University Press, Cambridge, United Kingdom and New York.
  11. Traub, K.-P., 2003. Geomedical Information Systems. The Application of GIS to Health Mapping Case Hamburg. Geoinformatics 6, pp. 20–23.
  12. Traub, K.-P., 2004. Geoinformationssysteme im Gesundheitswesen. Einfuhrung und praktische Anwendung. Wichmann, chapter Die Untersuchung der r?aumlichen Verbreitung von Gesundheitseinrichtungen mit GIS am Beispiel Hamburg, pp. 241–255.
  13. Spatenkova, O. and Krisp, J., 2007. The Use Of Contingency Tables To Value Variables For Spatial Models. In: The 5th International Symposium on Spatial Data Quality, Enschede, The Netherlands.
  14. Spatenkova, O., Dem?sar, U. and Krisp, J. M., 2007. Selforganising maps for exploration of spatio-temporal emergency response data. In: I. Maynoth (ed.), Processings of Geocomputation 2007.
  15. Whittingham, M. J., Stephens, P. A., Bradbury, R. B. and Freckleton, R. P., 2006. Why do we still use stepwise modelling in ecology and behaviour Journal of Animal Ecology 75, pp. 1182–1189.