

|
| Figure 1. Schematic genetic algorithm |
|
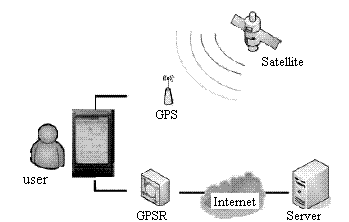
| Figure 2. The intelligent driving system |
| Minimize | 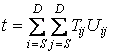 |
subject to |
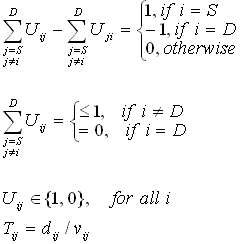
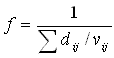
|
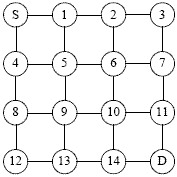
| Figure 3. Virtual map of Square matrix. |
| Number of chromosome |
Number of nodes | |||
| 16 | 64 | 256 | 1024 | |
| 20 | 3.31 | 5.19 | 9.38 | 13.97 |
| 40 | 5.06 | 7.29 | 9.95 | 17.33 |
| 60 | 6.33 | 8.18 | 10.59 | 18.21 |
| 80 | 6.58 | 9.22 | 11.16 | 18.30 |
| 100 | 6.60 | 10.27 | 12.04 | 18.38 |
| 120 | 6.64 | 10.46 | 12.44 | 18.48 |
| 140 | 6.71 | 11.64 | 13.27 | 18.77 |
| 160 | 6.89 | 11.92 | 14.08 | 19.05 |
| Number of chromosome |
Number of nodes | |||
| 16 | 64 | 256 | 1024 | |
| 40 | 12% | 34% | 47% | 56% |
| 80 | 3.6% | 23% | 44% | 52% |
| 160 | 1.2% | 18% | 39% | 51% |
| 320 | < 1% | 13% | 36% | 51% |
| 640 | < 1% | 7% | 31% | 49% |
| 1280 | < 1% | 5% | 26% | 48% |
| Number of chromosome |
Avg. number of generation |
Avg. difference |
| 40 | 22 | 223% |
| 80 | 26 | 180% |
| 160 | 28 | 103% |
| 320 | 29 | 86% |
| 640 | 31 | 68% |
| 1280 | 33 | 48% |