A PSEUDO GENETIC ALGORITHM FOR SOLVING BEST PATH PROBLEM
S. Behzadi, Ali A. Alesheikh
Dept. of GIS, Faculty of Geodesy and Geomatics Engineering, K.N. Toosi University of Technology Valiasr Street, Mirdamad Cross, Tehran, P.C. 19967-15433 -
behzadi@sina.kntu.ac.ir, alesheikh@kntu.ac.ir
Source of information: http://isprsserv.ifp.uni-stuttgart.de/proceedings/XXXVII/congress/2_pdf/2_WG-II-2/15.pdf
KEY WORDS: Genetic Algorithm, Shortest path problem, Mutation, Crossover, Pseudo GA.

ABSTRACT

    Within the last few decades, there has been exponential growth in the research, development, and utilization of Geospatial Information Systems (GIS). While GISs have been developed to challenge most types of spatial analysis problems, many of the more complex spatial problems are still beyond their current capabilities to solve. These types of problems often encounter large search spaces with large numbers of potential solutions. In such cases, standard analytical techniques typically cannot find optimal solutions to the problem within practical temporal and/or computational limits. One such problem within the field of spatial analysis is that of the routing problem. This paper focuses on the development of algorithmic solutions for the best path problem. Finding optimum path has many practical applications within the fields of operations research, logistics, distribution, supply chain management and transportation. In general, best path routing involves finding efficient routes for travelers along transportation networks, in order to minimize route length, service cost, travel time, number of vehicles, etc. This is a combinatorial optimization problem for which no simple solutions exist. As an alternative, solution techniques from the field of evolutionary computation is implemented and tested for solving instances of the best path. The field of evolutionary computation (EC) has developed to integrate several previously researched fields of related study into one. The sub-fields of EC include genetic algorithms, evolutionary programming, evolutionary strategies, and genetic programming. EC uses computational techniques that are analogous to the evolutionary mechanisms that work within natural biological systems, such as natural selection (i.e., survival of the fittest), crossover, mutation, etc. Within EC, these operators are used as a means of quickly evolving optimal or near-optimal solutions to a problem within a computational framework designed to represent a relevant search space. This paper scientifically reviews evolutionary algorithms in solving GIS problems. Based on their advantages and drawbacks of the methods a new algorithm called pseudo GA is developed. The algorithm is tested for various case studies. The results are presented and discussed. The result of performance analysis of the new algorithm is encouraging.

1. INTRODUCTION

    Genetic algorithms are inspired by Darwin's theory about evolution [3]. Solution to a problem solved by genetic algorithms is evolved. The genetic algorithm is a method for solving optimization problems that is based on natural selection, the process that drives biological evolution. The genetic algorithm repeatedly modifies a population of individual solutions. At each step, the genetic algorithm selects individuals at random from the current population to be parents and uses them produce the children for the next generation. Over successive generations, the population "evolves" toward an optimal solution. Algorithm is started with a set of solutions (represented by chromosomes) called population. Solutions from one population are taken and used to form a new population. This is motivated by a hope, that the new population will be better than the old one. Solutions which are selected to form new solutions (offspring) are selected according to their fitness – the more suitable they are the more chances they have to reproduce [4].
    This is repeated until some condition (for example number of populations or improvement of the best solution) is satisfied.
The following summarizes how the genetic algorithm works [2]:
  1. The algorithm begins by creating a random initial population.
  2. The algorithm then creates a sequence of new populations, or generations. At each step, the algorithm uses the individuals in the current generation to create the next generation. To create the new generation, the algorithm performs the following steps:
    1. Scores each member of the current population by computing its fitness value.
    2. Scales the raw fitness scores to convert them into a more usable range of values.
    3. Selects parents based on their fitness.
    4. Produces children from the parents. Children are produced either by making random changes to a single parent – mutation – or by combining the vector entries of a pair of parents – crossover.
    5. Replaces the current population with the children to form the next generation.
  3. The algorithm holds when one of the stopping criteria is met.
    The genetic algorithm differs from a standard optimization algorithm in two main ways, as summarized in the following table [2].

Standard Algorithm Genetic Algorithm
Generates a single point at each iteration. The sequence of points approaches an optimal solution. Generates a population of points at each iteration. The population approaches an optimal solution.
Selects the next point in the sequence by a deterministic computation. Selects the next population by computations that involve random choices.
    Table 1. the comparison between Standard Algorithm and Genetic Algorithm

    In this paper All to All shortest path will be solved. In this approach all parameters in Genetic algorithm will be described base on their rules in a Standard algorithm.

2. IMPLIEMENTATION

2.1 Design

    Each town in the map is given a unique integer value index from 1…………N, where, N is the number of cities in the map. Each individual is designed to represent a solution for the problem and it should not contain repeated town indices. The length of the individual is chosen to be equal to the number of towns in the total map; since there may be cases such that the shortest path may contain the total number[1].
    For a map with N number of cities the gene length is equal to N, where Ti is the ith town in the map.
    [T1, T2… T (N-1), TN]

2.2 Coding

    Permutation encoding is used in this problem. In permutation encoding, every chromosome is a string of numbers, which represents the number of towns in a sequence. The number of towns in each chromosome is not equal[5].

2.3 Initial population

    In this problem, there is not a certain number for initial population, and the initial population will be generated base on the criterion of the problem.

2.4 Individual generation for the initial population

    Initial population is generated base on the weighted matrix of the network. The initial population is a set of individuals that their lengths equal to two. The first gene of each individual is the source point and another gene is destination point.
    If there exists a rout between i, j , an individual such as [i, j] is generated. All individuals at first generation are generated this way. Individuals are generated base on the weighted matrix on the connections between points. Some of these individuals are shown in Figure 1.
Figure 1. Some of the individuals at first generation

2.5 Fitness function

    The fitness function of each individual at first generation is the weight of the connected line between two nodes. For example (i,j)=Cij is one individual at first generation that the length of it is 2 and it represents the connection between i,j as Cij is its fitness function.

2.6 Fitness Scaling

    Fitness scaling converts the raw fitness scores that are returned by the fitness function to values in a range that is suitable for the selection function. The selection function uses the scaled fitness values to select the parents of the next generation. The selection function assigns a higher probability of selection to individuals with higher scaled values. After creating the initial population, fitness values for each individual are calculated. In this research, proportional scaling is used to make the scaled value of an individual proportional to its raw fitness score[2].

2.7 Crossover operator

    The crossover operator in this method is different than currently used ones. The individuals at first generation are designed by weighted matrix. Normally, individuals are generated by the following equations:
Individuals at first generation
…
Individuals at (k-1)th generation
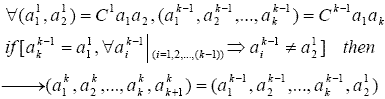    The individuals at first and k th generations are used to generate individuals at k th generation. Their combinations are represented by the following equations:
(1)
    The best individuals are selected at each generation. This selection is represented by the following equations:
(2)
    This selection is represented in Figure 2.
Figure 2. The comparison between two routs in a generation

    Then the best individual which has the minimum weight between the individuals and have the same start and end points are selected. Therefore, suitable population in each generation is determined. The number of the individuals at each generation is different.
    The crossover operator can be used between the individuals at current generation and other generations expect second generation.

2.8 Migration

    Migration specifies how individuals move between subpopulations. When migration occurs, the best individuals from one subpopulation replace the worst individuals in another subpopulation. Individuals that migrate from one subpopulation to another are copied. They are not removed from the source subpopulation[2]. The process of migration in this approach is both forward and backward. At first, all individuals in previous generations migrate to current generation (forward migration). Individuals were survived in the previous generations are the best individuals in their generations. The comparison is done between current individuals and migrated individuals then the best individual will be survived and others will be omitted. The survived individual may be contained current generation or previous generations. If individuals are contained previous generations, they will come back to their generations (backward migration). The comparisons between individual are represented by following equations:
(3)
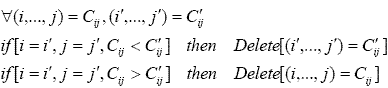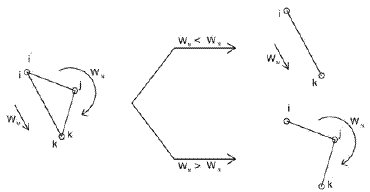
    These comparisons are showed in Figure 3.
Figure 3. The comparisons between two generations

    If the weights of two individuals are equal, they both can be survived or one of them can be omitted by other criteria such as other weights.
    The network witch has n node then there exist (n-1) routs to other nodes from each node and n(n-1) will be created for such network, therefore, the total number of individuals in this network is n(n-1).

2.9 Termination criteria

    In Genetic algorithm, there are some criteria to stop the algorithm like the number of iterations [6], stall generations, stall time limit and etc. If one of these criterions is occurred, the algorithm stops.
    In this new algorithm, there exist two termination criteria:
  1. If all individuals in a new generation is omitted by migrated individuals, then there are no individuals to generate new generation, hence, the algorithm will stop.
  2. When an individuals with the length of n genes are created. These individuals are in (n-1) generations. In this case there is no node (gene) in the area to connect to the chromosome because all nodes are in the chromosome, therefore, the algorithm will stop.
    If this algorithm is used for a real network, the first stop criterion is usually happened because it rarely happens that the best rout have passed throw all node.

3. EXPERIMENTS

    To evaluate the performance of the outlined method, we performed some experiments using actual road maps of parts of Tehran, the capital city of Iran (Figure.5). In this problem, the lengths of the arcs are considered as weights of the arcs. The objective was to minimize the total weight of path. The result of this experiment is shown in Fig. 5.
Figure5. a. A part of the tested map           b. Start and End point and the shortest path

4. CONCLUSIONS

    In this paper, a new method of finding the best path problem was proposed. In this method all parameters in Genetic algorithm were described base on their rules on Standard algorithm. By using this method, All to All shortest path was solved. All to All shortest Path problem is inspired by GAs. In this algorithm all parameters of GAs are used but the usage of the parameters are base on the deterministic computation. The result of solving the best path problem shows that it rarely happen that the best rout have passed throw all nodes then the steps of this algorithm are less than n steps that happen in Dijkstra’s algorithm. The flexibility of this algorithm is high and it can be used to solve other problems such as Travelling Salesman Problem (TSP), finding closest facility, finding service area and etc. The speed of solving the problem can be modified by using a series of conditions like changing this algorithm to 1 to All.

5. REFERENCES

[1] Abeysundara S., Giritharan B., Kodithuwakku S., 2005, A Genetic Algorithm Approach to Solve the Shortest Path Problem for Road Maps, Proceedings of the International Conference on Information and Automation, pp. 272-275.
[2] "Genetic Algorithm and Direct Search", http://www.mathworks.com/access/helpdesk/help/toolbox/gads/ (accessed 30 July. 2007)
[3] Hosseinali F., Alesheikh Ali A., 2008, Weighting Spatial Information in GIS for Copper Mining Exploration, American Journal of Applied Sciences. Vol. 5, No. 9, pp. 1187- 1198.
[4] "Introduction to Genetic Algorithms", http://cs.felk.cvut.cz/~xobitko/ga/ (accessed 7 Jun. 2007)
[5] Levitin G., Rubinovitz J., Shnits B., 2006, A genetic algorithm for robotic assembly line balancing, European Journal of Operational Research 168 (3) 811–825
[6] Yang H., Yang C., Gan L., 2006, Models and algorithms for the screen line-based traffic-counting location problems, Computers & Operations Research, 33, pp.836–858