M. R. Delavar, F. Samadzadegan, P. Pahlavani. A GIS-Assisted Optimal Urban Route Finding Approach Based On Genetic Algorithms

A GIS-ASSISTED OPTIMAL URBAN ROUTE FINDING APPROACH BASED ON GENETIC ALGORITHMS

M. R. Delavar, F. Samadzadegan, P. Pahlavani

Source of information: http://www.isprs.org/proceedings/XXXV/congress/comm2/papers/144.pdf

KEY WORDS: GIS, SDSS, Genetic Algorithm, Route Finding, Vehicle Routing Problem

ABSTRACT:

Network analysis in geospatial information system (GIS) provides strong decision support for users in searching optimal route, finding the nearest facility and determining the service area. Searching optimal path is an important advanced analysis function in GIS. In present GIS route finding modules, heuristic algorithms have been used to carry out its search strategy. Due to the lack of global sampling in the feasible solution space, these algorithms have considerable possibility of being trapped into local optima. This paper addresses the problem of selecting route to a given destination on an actual map under a static environment. The proposed solution uses a genetic algorithm (GA). A part of an arterial road is regarded as a virus. We generate a population of viruses in addition to a population of routes. A customized method based on a genetic algorithm has been proposed and successfully implemented in an area in the north-east of Tehran using the optimal combination of viruses.

1. INTRODUCTION

Decisions are often evaluated on the basis of quality of the processes behind. It is in this context that geospatial information system (GIS) and spatial decision support system (SDSS) increasingly are being used to generate alternatives to aid decision-makers in their deliberations. The intelligent transport system (ITS) can carry and gather very useful information for delivery to users and perform other useful functions to deal with the travel. The introduction of subsystems that support the decision making to suit changing conditions is a logical important step in providing systems with improved functionalities.
Unfortunately, GIS and SDSS typically lack formal mechanisms to help decision-makers explore the solution space of their problem and thereby challenge their assumptions about the number and range of options available. We describe the use of a genetic algorithm to generate a range of options available. The ability of genetic algorithms to search a solution space and selectively focus on promising combinations of criteria makes them ideally suited to such complex spatial decision problems.
Routing problems in car navigation systems are search problems for finding an optimal route from an origin to a destination on a road map within a time limit. In a practical system, when traffic congestion changes during driving, the route should be re-evaluated before the car reaches the next intersection. A representative solution to these search problems is the Dijkstra algorithm (DA), (Golden, 1976). As the DA is an exact algorithm it always determines the optimal route but cannot guarantee that realistic deadlines will be met. In contrast, as genetic algorithms always have solutions in a population during a search, they can provide alternative routes using other solutions in the shortest time.
A method has been proposed in this paper for using a genetic algorithm to find the easiest-to-drive and quasi-shortest route to reach a destination within a given time. It can be used to produce and choose candidate routes that guarantee the meeting of deadlines and satisfy constraints regarding ease of driving.

2. SOLVING CONSTRAINT SATISFACTION PROBLEMS USING GA

Genetic algorithm is a computational model simulating the process of genetic selection and natural elimination in biologic evolution. Pioneering work in this field was conducted by Holland in the 1960s (Holland, 1975; Coley, 1992).
As a high efficient search strategy for global optimization, genetic algorithm demonstrates favorable performance on solving the combinatorial optimization problems. With comparing to traditional search algorithms, genetic algorithm is able to automatically acquire and accumulate the necessary knowledge about the search space during its search process, and self-adaptively control the entire search process through random optimization technique. Therefore, it is more likely to obtain the global optimal solution without encountering the trouble of combinatorial explosion caused by disregarding the inherent knowledge within the search space. It has been used to solve combinatorial optimization problems and non-linear problems with complicated constraints or non-differentiable objective functions. It necessitates the application of genetic algorithm into GIS route finding algorithms.
The computation of usual genetic algorithm is an iterative process that simulates the process of genetic selection and natural elimination in biologic evolution. For each iteration, candidate solutions are retained and ranked according to their quality. A fitness value is used to screen out unqualified solutions. Genetic operators, such as crossover, mutation, translocation and inversion, are then performed on those qualified solutions to estimate new candidate solutions of the next generation. The above process is carried out repeatedly until certain convergent condition is met.
And finally, GA is a general search method (Goldberg, 1989). It uses analogs of genetic operators on a population of states in a search space to find those states that have high fitness values. In optimization problems, genetic operators and coding methods are designed in advance so that the individuals may satisfy the constraints. In contrast, the objective of constraint satisfaction problems (CSPs) is to find an individual that satisfied constraints as the fitness value. Search in usual GA, based on neo-Darwinian evolutionary theory is conducted by crossover and mutation. Crossover is generally considered a robust search means. Offspring may inherit partial solutions without conflict from their parents, but no information to decide which genes are partial solutions is available. From a searchstrategic point of view this means that variables are randomly selected and then values which will be assigned to them are also randomly selected from genes contained within a population. Therefore search by crossover in GA can not be considered efficient. Furthermore, mutation is a random search method itself. When we think about efficiency of global search that is the most important characteristic of GA; we must admit that the rate of search is low, because GA stresses random search rather than directional search. It can be considered that the above problem is directly inherited from problems of the neo-Darwinian evolutionary theory.
In the following sections, we first explain our basic strategies. Next, we describe the fitness function, genetic operators. Finally, we show the experimental results using an actual road map.

3. STRATEGIES

Due to the advantages and disadvantage we mentioned in the previous section, we plan to improve the rate of search by giving direction to evolution that is search using crossover and virus theory of evolution (Nakahara et al., 1986).
Domain specific knowledge, as partial solutions of problems, is usually introduced into an initial population. Partial solutions are considered to be viruses, and a population of viruses is created as well as a population of individuals.
Our solution using the GA is based on the following basic strategies:

Any segment of an arterial road is regarded as a main virus. We generate a population of viruses in addition to a population of routes.
Only routes that include viruses are generated as the initial population. If two of the same routes are produced in the population, one is removed.
Minimal generation gap (MGG) model (Satoh et al., 1996; Ono et al., 1999) for alternation of generations. Mutation does not occur in the proposed method.

3.1. Problem constraints

GA has been successfully applied to many NP-hard problems. When the problem has hard constraints, some candidate solutions are infeasible. This problem is generally addressed in three ways:

Avoiding infeasible solutions during the search process.
Penalizing infeasible solutions.
Extracting feasible solutions after carrying out the search using populations that may contain infeasible candidate solutions.

The constraints on this particular problem can be grouped into the following two categories:

Fixed constraints: are always enforced, irrespective of the composition of the current solution. For example to select arterial and/or wide roads to decrease the number of turns and so on.
Dynamic constraints: are enforced based on the composition of the current solution. For example, to select the roads where the traffic restrictions are not imposed and to select the roads not congested with traffic and so on.

In this stage of the development, our algorithm uses a directed graph representation that embeds some static constraints.

4. PROPOSED METHOD

4.1. Algorithm

Figure.1 shows the general steps of the algorithm. Details are given in the following sections.

input map and map database
input origin and destination
initialize a population of viruses
initialize a population of individuals (routes). Set Generation= 1
for generation = 1 to Number of Generation (repeat until meeting deadline) {
calculate fitness values of individuals
select two individuals at random
single-point crossover
MGG
}

Figure 1. Algorithm of the proposed method

4.2. Coding and fitness

Repairing infeasible candidate solutions may incur significant computational expense, but omitting them from the search process may leave the search space disconnected, preventing satisfactory optima from being reached. Computationally efficient search can be carried out by choosing a representation that implicitly excludes infeasible candidate solutions, without hindering the search process from visiting different parts of the search space.
Variable-length chromosomes (routes) and their genes (intersections) have been used for encoding the problem. A chromosome of the proposed GA consists of sequences of positive integers that represent the IDs of nodes through which a routing path passes. In the other hand, we regard each route from an origin to a destination as an individual for the GA and express it as a sequence of intersections with directions.
The fitness of a route is evaluated using the length of the route, the time required for a car to travel along it and the ease of driving.
Penalties for violations are defined for each constraint. An amenity can be calculated from a penalty if the route violates constraints.
We regard the route with the lowest number of penalties as the best one for drivers.

4.3. Population initialization

In general, there are two issues to be considered for population initialization of GA: the initial population size and the procedure to initialize population (Goldberg, 1989; Hue, 1997). It was felt that the population size needed to increase exponentially with the complexity of the problem (i.e., the length of the chromosome) in order to generate good solutions. Recent studies have shown, however, that satisfactory results can be obtained with a much smaller population size. To summarize, a large population is quite useful, but it demands excessive costs in terms of both memory and time (Goldberg, 1989; Harik, 1999). As would be expected, deciding adequate population size is crucial for efficiency.
Secondly, there are two ways to generate the initial population: heuristic initialization and random initialization (Hue, 1997). In this method, we select viruses within the rectangle on the map with a diagonal that links the origin and the destination and we name them ‘main-viruses’.
To generate the initial population, a virus is randomly selected from the population of viruses. Next, both the routes from the origin to the virus and the route from the virus to the destination are generated by using an RTA* algorithm (Korf, 1990). Finally, the route that combines these two routes with the virus becomes an individual. This procedure is repeated for all of the main viruses.

4.4. Selection and crossover

The selection (reproduction) operator is intended to improve the average quality of the population by giving the high-quality chromosomes a better chance to get copied into the next generation (Goldberg, 1989; Hue, 1997).
Crossover examines the current solutions in order to find better ones (Goldberg, 1989; Hue, 1997). Physically, crossover in the routing problems plays the role of exchanging each partial route of the two chosen chromosomes in such a manner that the offspring produced by the crossover will only be one route. This dictates selection of one-point crossover as a good candidate scheme for the proposed GA. One partial route connects the source node to an intermediate node and the other partial route connects the intermediate node to the destination node. But the mechanism of the crossover is not the same as that of the conventional one-point crossover.
In the proposed scheme, we use the minimal generation gap (MGG) model (Satoh et al., 1996; Ono et al., 1999) for alternation of generations. In this model, two routes are replaced by crossover with each new generation and so two evaluations of fitness are required between generations.
Mutation is not used in this method (Figure 2).

Figure 2. Minimal Generation Gap (MGG) model

Here are the directions for the process.

Take two individuals at random from the population for use as parents.
Apply simple crossover to the parents to produce offspring, where the crossover site is at an intersection which they have in common. If there is no such common intersection, then go to the previous step.
From the parents and their children, we select the best individual (elite route) and the random one using the roulette wheel technique. With them the original parents are replaced.

In this model, original parents are two individuals, and replacing individuals are also two. Then we leave the elite individual for progress in solving a problem, and leave a random individual for maintaining diversity of population. It should also be noted that this model only uses fitness values of each individual. It makes the computational load of the operation light.

5. EXPERIMENTS

To evaluate the performance of the outlined method, we performed experiments using actual road maps of Tehran at a scale of 1:2000 provided by Miaad Andisheh Saz, Research and Development Company, in Iran.
Table 1 shows the characteristics of the maps used in the following experiments, where the nodes correspond to the intersections and Table 2 shows the experimental results achieved from the map. In addition, each result given bellow was performed on AMD Athlon(tm) XP 1600+ (1.40 GHz), (Figures 3 and 4).

Table 1. Characteristics of the map used

	Number of viruses	Number of links	Number of nodes
Map	121	3993	3071

Table 2. Experimental results achieved from the map

	Time (min.)	MRR (%)	Turns	C-Time(sec.)
GA using 'main-viruses'	53	68	8	11
GA using all viruses	50	73	6	70

where Time: time required for the car to reach its destination.
MRR: rate of main road length to route length.
Turn: the number of turn.
C-Time: Calculation time.

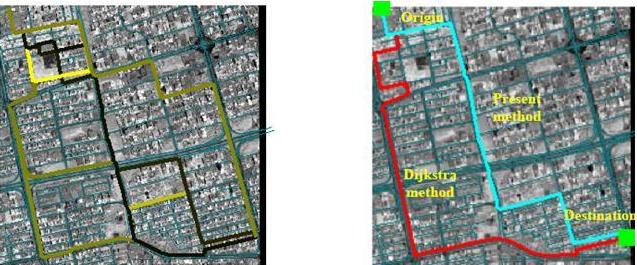
Figure 3. A part of the tested map Figure 4. A part of the tested map and
Initial population and examples of routes

6. CONCLUSIONS

As a high efficient search strategy for global optimization, genetic algorithm demonstrates favorable performance on solving the combinatorial optimization problems. The best route selection problem in network analysis can be solved with genetic algorithm through efficient encoding, selection of fitness function and various genetic operations. Crossover is identified as the most significant operation to the final solution.
The experience shows that the designed implementation method is effective in terms of computation time and complexity. Tests of route selection for a moderate complicated network are conducted and their results show the efficiency of the algorithm and support our analyses. Further efforts will be made on the following items:

Enhancing the adaptability of the algorithm under dynamic constraints.
Expanding the applications of the algorithm into broader GIS topics.

REFERENCES

Coley, D.A., 1992. An Introduction to Genetic Algorithms for Scientists and Engineers, World Scientific.
Goldberg, D.E., 1989. Genetic Algorithms in Search, Optimization and Machine Learning. Addison Welsey Publishing Company.
Golden B., 1976. Shortest-Path Algorithms – A comparison, Operations Research, Vol.24, No. 9, pp. 1164-1168.
Harik G., Cantu-Paz E., Goldberg D. E. and Miller B. L., 1999. The Gambler’s Ruin Problem, Genetic Algorithms, and the Sizing of Populations, Evol. Comput., Vol. 7, No. 3, pp. 2311-253.
Holland J. H., 1975. Adaptation in Nature and Artificial Systems. The University of Michigan Press, Reprinted by MIT Press, 1992.
Hue, X., 1997. Genetic Algorithms for Optimization: Bachground and Applications. Edinburgh Parallel Computing Centre, Univ. Edinburgh, Scotland, Ver 1.0.
Korf, R. E., 1990. Real-time Heuristic Search, Artif. Intell., Vol. 42, No. 2-3, pp. 189-211.
Nakahara H., Sagawa T. and Fuke T., 1986. Virus theory of evolution. Bulletin of Yamanashi Medical College, Vol.3, pp. 14-18.
Ono, I., Kita H. and Kobayashi S., 1999. A Robust Real-Coded Genetic Algorithm Using Unimodal Normal Distribution Crossover Augmented by Uniform Crossover: Effects of Self-Adaptation of Crossover Probabilities, Proc. GECCO ’99, pp. 496-503.
Satoh, H., Yamamura M. and Kobayashi S., 1996. Minimal Generation Gap Model for GAs Considering Both Exploration and Exploitation, Proc. IIZUKA ’96, pp. 494-497.