
|
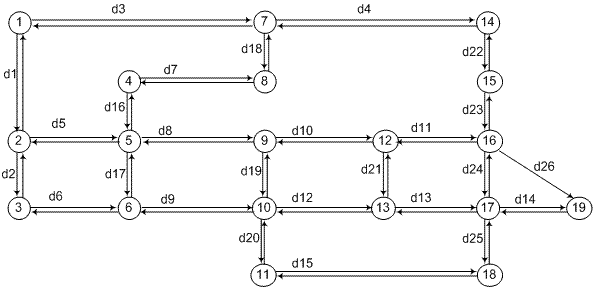
| Рис 1 Модель представления транспортных магистралей города |

|
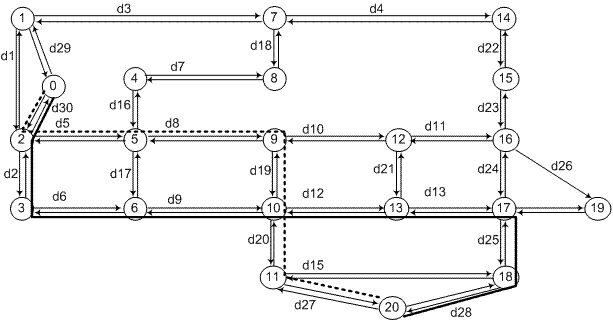
| Рис 2 Добавление искусственных перекрестков |
| X = {p0, p1, p2, … , pn} | (1) |
| H = {X1, X2, ..., Xm}, | (2) |

|
| Рис 3 Пример выполнения оператора селекции |
|
| Рис 4 Результат выполнения оператора кроссовера |