ГЕНЕТИЧЕСКИЙ АЛГОРИТМ ДЛЯ ОПРЕДЕЛЕНИЯ МИНИМАЛЬНОГО ВРЕМЕНИ ПУТИ В ИНТЕЛЛЕКТУАЛЬНЫХ ТРАНСПОРТНЫХ СИСТЕМАХ
Авторы: Chu-Hsing Lin, Jui-Ling Yu, Jung-Chun Liu, Chia-Jen Lee
Перевод с английского: Казакова Ю. С.
Источник: http://dado.thu.edu.tw/files/teacher/285.pdf

Аннотация

    Система навигации маршрута, которая предоставляет рекомендации вождения, основанные на транспортной информации о начальной точке и месте назначения, стала очень популярной вместе с продвижением мобильных устройств и глобальной системы позиционирования. Так как точность и эффективность указания маршрута зависит от точности дорожной ситуации, система навигации должна включать в расчет дополнительные переменные, такие, как транспортные потоки в реальном времени и допустимые скорости движения транспортных средств. Поскольку в системе навигации увеличивается количество рассматриваемых переменных, вычислительная стоимость также возрастает. Так как мобильные устройства имеют ограниченные ресурсы, не представляется возможным использовать их для вычисления точного оптимального решения с использованием некоторых известных алгоритмов, таких, как алгоритм Дейкстры, который обычно используется для поиска кратчайшего пути на карте с умеренным числом вершин.
    Чтобы решить эту проблему, мы предлагаем использовать генетический алгоритм для уменьшения роста вычислительных затрат. Мы используем генетический алгоритм для определения минимального времени движения с различными сценариями реальных условий дорожного движения и различной скоростью движения транспортного средства. Эффективность генетического алгоритма наглядно демонстрируется в применении на реальной карте современного города с очень большим числом вершин.

     Ключевые слова: генетический алгоритм, интеллектуальная транспортная система, оптимальный маршрут, портативное устройство, интеллектуальная система навигации

1. Введение

    Стало обычной практикой использовать КПК для указания маршрута [1-2]. Как правило, кратчайший путь определяется системами навигации, чтобы сообщить пользователям, как достигнуть места назначения от исходного пункта. В зависимости от реальной ситуации, включая транспортные скопления, дорожные условия, ограничения скорости, и поведение водителей, на предложенном маршруте время пути может быть сэкономлено или нет.
    Кратчайший путь, определяемый системами навигации маршрута не обязательно оптимальный путь, поскольку он рассчитывается главным образом по кратчайшему расстоянию, в то время как другие переменные, например, пробки, ограничения скорости, могут оказывать существенное влияние и должны быть включены в вычисления. Учитывая большое число переменных трафика вычислительные затраты могут занять слишком много времени и ресурсов портативных устройств. В общем случае, вычислительная мощность и память портативных устройств ограничена. Один из способов решить эту проблему, производить все расчеты на хост сервере, но связь между портативными устройствами и хост сервером может быть нарушена. Альтернативным методом является использование некоторого алгоритма, который может предоставить приблизительное решение со сравнительно низкими вычислительными затратами. В этой статье мы предлагаем использовать генетический алгоритм для поиска оптимального пути. Поскольку мы принимаем во внимание допустимые скорости движения транспортных средств, системы навигации маршрутов используют кратчайшее время движения, а не кратчайшее расстояние пути.
    Остальная часть статьи организована следующим образом. В разделе 2 приводится справочная информация. В разделе 3 определена проблема определения минимального времени движения. Постановка эксперимента и результаты моделирования представлены в разделе 4. Раздел 5 содержит выводы.

2. Предпосылки

А. Задача определения кратчайшего пути

    В теории графов, задача определения кратчайшего пути может быть обобщена как задача определения единственного кратчайшего пути от исходной вершины ко всем другим вершинам в графе. Известные алгоритмы для решения этой задачи: алгоритм Дейкстры и алгоритм Форда-Беллмана.
    Алгоритм Дейкстры определяет кратчайший путь, когда веса ребер неотрицательны, что применимо к условиям системы навигации маршрута. Мы будем использовать алгоритм Дейкстры для поиска кратчайшего времени движения, когда число вершин не слишком велико. Время выполнения алгоритма Дейкстры, храня вершины в обычном связном списке, – O (| V |2 + | E |), где | V | – число вершин и | E | – число ребер. Время работы становится неприемлемым, когда количество вершины слишком велико. В такой ситуации для нахождения приближенных решений могут быть использованы другие альтернативные методы. Генетический алгоритм – один из них.

B. Генетический алгоритм

    Генетический алгоритм – техника поиска, позволяющая найти точные или приблизительные решения [3-10]. Она возникла из теории эволюции в природе. В 1975, Джон Х. Холланд разработал генетический алгоритм в книге под названием «Адаптация в Естественных и Искусственных Системах». Генетические алгоритмы широко применяются в различных приложениях, включая генную биологию, экономику, теорию игр, распознавание образов, нейронные сети, теорию нечетких множеств и т.д.
    На рис.1 показаны этапы генетического алгоритма, которые описываются следующим образом:     Чанг и др. в 2002 году [6] предложили использовать генетический алгоритм для решения задачи нахождения кратчайшего пути. Проблема описана следующим образом:
    Сеть с множеством звеньев может быть представлена как ориентированный граф G = (N, A), где N обозначает множество из n узлов (вершин) и A обозначает множество ребер. Матрица стоимости обозначена как C = [Cij], где Cij соответствует стоимости проезда от узла i к узлу j. Начальная точка (источник) – S, и место назначения – D. Индикатор связи, Iij, указывает, существует ли маршрут между узлом i и узлом j. Если маршрут существует, то Iij = 1, иначе, Iij = 0.
    Они показывают, что с помощью генетического алгоритма для сети с 20 узлами через девять поколений находится оптимальное решение. Генетический алгоритм быстро сходится и ему требуется всего несколько поколений, чтобы найти оптимальное решение. Поскольку число узлов превышает 20, вычислительное время применения генетического алгоритма меньше, чем время применения Алгоритм Дейкстры. Таким образом, более целесообразно использовать генетический алгоритм для поиска оптимального пути на сложных реальных картах с тысячами узлов с использованием мобильных устройствах с ограниченными ресурсами.
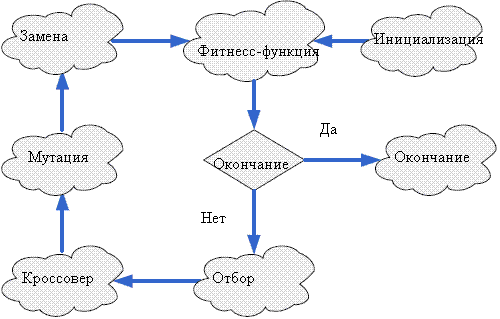
Рисунок 1. Схема генетического алгоритма
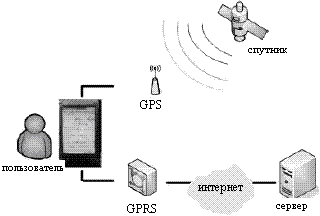
C. Интеллектуальная транспортная система (ИТС)

    Интеллектуальная транспортная система (ИТС) предоставляет водителям руководство маршрута и картографическую информацию, и она может быть использована для поддержки интеллектуальной системы навигации с помощью индикации направления или информации поступающей от пользователей [11] [12] [15]. Как показано на рисунке 2, интеллектуальные системы навигации направляют водителя к месту назначения, обновляя оптимальный маршрут путешествия согласно оперативной транспортной информации.
Рисунок 2. Интеллектуальная система навигации
3. Определение минимального времени движения

    Задача определения минимального времени движения (МВД) может быть сформулирована как модель программирования. Список обозначений данной математической модели задается следующим образом:
    Параметры:
        N           множество всех узлов
        A           набор всех ребер
        S           узел-источник, ∈ N
        D           узел-назначение, ∈ N
        i,j           индекс узла, i,j , ∈ N
        <i,j >     направление от узла i к узлу j
        Eij         связь узлов i,j
        dij         расстояние от узла i к узлу j
        vij         скорость на участке от узла i к узлу j

    Переменные:
        Tij           cвремя движения от узла i к узлу j, ∈ R
        Uij           бинарная переменная, 1, если связь от узла i к узлу j существует, 0 иначе
        T             общее время движения, ∈ R+

    В традиционной задаче определения кратчайшего пути, стоимость между узлом i и узлом j – это расстояние dij. Принимая во внимание ограничение скорости, vij, которое является самой высокой скоростью движения от узла i к узлу j, время движения может быть определено как Tij = dij ⁄ vij. Заменив стоимость расстояния стоимостью времени, мы можем использовать алгоритм Дейкстры для поиска минимального времени пути следующим образом:
Минимизировать 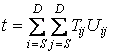при условии
   

    Чтобы найти минимальное время пути, мы также используем следующие шаги на основе генетического алгоритма, предложенные Чангом и др.: [6] [13] [14]

    Шаг 1. Представление хромосомы:
    Используются хромосомы с различными длинами. Максимальная длина N, которая может быть установлена в первую очередь. Хромосомы начинают в S и заканчивается в D. Например, мы можем представить маршрут как хромосому (S → N1 → N2 → … → Nk-1 → Nk → D).
    Шаг 2. Инициализация популяции:
    Хромосомы первого поколения генерируются с учетом размера популяции и процедуры инициализации. Могут применяться эвристическая инициализация или случайная инициализация.
    Шаг 3. Определение фитнесс-функции:
    Фитнесс-функция определяется как
   
    Где f представляет значение фитнесс-функции хромосомы, dij – расстояние от узла i к узлу j, vij – допустимая скорость на участке от узла i к узлу j.
    Шаг 4. Выбор родителей:
    Используется попарный турнирный выбор без замены.
    Шаг 5. Кроссовер:
    Кроссовер осуществляется случайным поиском точки пересечения в двух хромосомах.
    Шаг 6. Мутация:
    Вероятности мутации устанавливаются в диапазоне от 5% до 10%. Она используется для создания новых маршрутов.
    Шаг 7. Завершение:
    Повтор процессов генерации до достижения условий окончания.

4. Экспериментальные исследования и результаты

    Мы использовали встроенную систему ARM 9 S3C2410 в качестве портативного устройства, а также настольный ПК в качестве ИТС сервера, которые обеспечивают допустимые скорости движения в зависимости от дорожных условий. Мы провели две серии экспериментов, один на виртуальной карте, представленной квадратной матрицей, и один на реальной карте города.
    Мы применили алгоритм Дейкстры и генетический алгоритм для расчета минимального времени движения. Но так как количество узлов возросло, размер памяти, требуемый для алгоритма Дейкстры, вышел за рамки ограниченные памятью встроенной системы. Таким образом, мы представим лишь экспериментальные результаты, применения генетического алгоритма.

4.1 Случай Матричной Карты

    Виртуальные карты, представленные квадратными матрицами, имели размеры 4x4, 8x8, 16x16, and 32x32.
    Как показано на рисунке 3, исходный узел находился в левом верхнем углу, а пункт назначения – в правом нижнем углу. Расстояния между узлами были зафиксированы и равны 20. Ограничения скорости варьировались от 2 до 10. Вероятность мутации была установлена 8%, а предел количества поколений был установлен на уровне 30. Все эксперименты были сделаны 1000 раз.
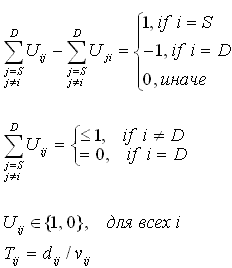
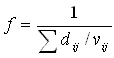
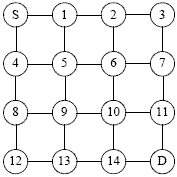
Рисунок 3. Виртуальная карта, представленная квадратной матрицей

    В таблице 1 представлено среднее число поколений для определения минимального времени пути. Видно, что генетический алгоритм сходится очень быстро, менее чем за 20 поколений, даже если число узлов возрастает до 1024. Также для сложной карты с тысячами узлов, среднее число поколений для сходимости генетического алгоритма достаточно мало для приложений реального времени.

    Таблица 1. Среднее число поколений для определения минимального времени пути
Количество
хромосом		 Количество узлов
16 64 256 1024
20 3.31 5.19 9.38 13.97
40 5.06 7.29 9.95 17.33
60 6.33 8.18 10.59 18.21
80 6.58 9.22 11.16 18.30
100 6.60 10.27 12.04 18.38
120 6.64 10.46 12.44 18.48
140 6.71 11.64 13.27 18.77
160 6.89 11.92 14.08 19.05

    Когда генетический алгоритм начинает сходиться, почти оптимальные маршруты найдены. В таблице 2 приведены средние разности приблизительного маршрута и точного маршрута. Видно, что когда число узлов мало, 16 или 64 узла в данном примере, приблизительные решения очень близки к точным решениям, и средняя разность составляет менее 5%. Кроме того, помогает увеличение числа хромосом. Но, когда число узлов велико, например, 1024 узлов, разница приближенных и точных решений возрастает до 50%.

    Таблица 2. Средняя разница приближенных и точных маршрутов (в %)
Количество
хромосом		 Количество узлов
16 64 256 1024
40 12% 34% 47% 56%
80 3.6% 23% 44% 52%
160 1.2% 18% 39% 51%
320 < 1% 13% 36% 51%
640 < 1% 7% 31% 49%
1280 < 1% 5% 26% 48%

4.2 Случай Реальной Карты

    Мы использовали карту города Тайчжун, Тайвань для экспериментов с реальной картой. Она содержит 8039 узлов и 5 уровней дорог в зависимости от ограничений скорости. Дороги с наибольшей скоростью классифицируются как LV5, и дороги с наименьшей скоростью классифицируются как LV1. Информация об ограничениях скорости предоставляется сервером ИТС в режиме реального времени.
    Результаты экспериментов приведены в таблице 3. Видно, что генетический алгоритм сходится относительно быстро даже с большими объемами данных, поэтому целесообразно использовать генетический алгоритм на мобильных устройствах для определения почти оптимального пути. Из таблицы также видно, что число хромосом критическое в случаях, когда число узлов очень велико. Благодаря увеличению числа хромосом от 40 до 1280, разница между приближенными и точными решениями, сократилась с 223% до 48%.

    Таблица 3. Результаты генетического алгоритма на реальной карте
Количество
хромосом		 Среднее число
поколений		 Среднее
отличие
40 22 223%
80 26 180%
160 28 103%
320 29 86%
640 31 68%
1280 33 48%

5. Выводы

    Системы навигации имеют очень широкое применение. Идеальная система навигации предоставляет не только информацию о кратчайшем пути, основанную на статической информации о расстоянии от исходной точки до назначения, но и предлагает динамические решения на основе информации, собранной ИТС от датчиков и пользователей. Подход определения минимального времени пути, с помощью генетического алгоритма на портативном устройстве, целесообразно использовать в системе навигации маршрутов.
    Вычислительная мощность и объем памяти мобильных устройств являются ограниченными. Поиск точного оптимального решения на них не практичен с огромным количеством данных о трафике. Генетический алгоритм может быть использован для поиска приближенных решений, он может эффективно находить почти оптимальные пути в сложных ситуациях, когда в расчет включены множество переменных, влияющих на движение.

6. Подтверждение

    Эта работа была частично поддержана Тайваньским Информационным Центром Безопасности, Национальным Советом Науки под грантами NSC-95-2218-E-001-001, NSC-95-2218-E-011-015, iCAST NSC96-3114-P-001-002-Y и NSC95-2221-E-029-020-MY3.

7. Ссылки

[1] Shaojun Feng and Choi Look Law, "Assisted GPS and its impact on navigation in intelligent transportation systems", in Proc. Intelligent Transportation Systems, 2002, pp. 926-931
[2] Victor Chang, "Web Service Testing and Usability for Mobile Learning", in Networking, International Conference on Systems and International Conference on Mobile Communications and learning Technologies, 2006, pp. 221-227
[3] Shubin Xu and James C. Bean, "A Genetic Algorithm for Scheduling Parallel Non-identical Bath Processing Machines", in Computational Intelligence in Scheduling, 2007, pp. 143-150.
[4] M. Munemoto, Y. Takai, and Y. Sato, "A migration scheme for the genetic adaptive routing algorithm", in Proc. IEEE Int. Symp. Circuits and Systems, 1999, pp. 137-140.
[5] J. Inagaki, M. Haseyama, and H. Kitajima, "A genetic algorithm for determining multiple routes and its applications", in Proc. IEEE International Symposium on Circuits and Systems, 1999, vol. 6, pp. 137-140
[6] Chang Wook Ahn and R.S. Ramakrishnal, "A Genetic Algorithm for Shortest Path Routing Problem and the Sizing of Populations", in Evolutionary Computation, IEEE Transactions, 2002, pp. 566-579.
[7] Mitsuo Gen and Lin Lin, "A New Approach for Shortest Path Routing Problem by Random Key-based GA", in Proc. Genetic and evolutionary computation, July 2006, pp. 1411-1412
[8] Zhenjiang Li, J. J. Garcia-Luna-Aceves, "Quality of service in wireline networks: A distributed approach for multi-constrained path selection and routing optimization", 2006
[9] Qinqfu Zhang and Yiu-Wing Leung, "An orthogonal genetic algorithm for multimedia multicast routing", in Evolutionary Computation, IEEE Transactions, 1999, pp. 53-62
[10] Yue Chengjun and Jing yuanwei, "Solving the Problem of the Link Optimizing and Delay-constrained Multicast Routing Based on GA", in Control Conference Chinese, 2006, pp. 1783-1786.
[11] Housroum H., Hsu T., Dupas R. and Goncalves G., "A hybrid GA approach for solving the Dynamic Vehicle Routing Problem with Time Windows", in Information and Communication Technologies, April 2006, pp. 787-792
[12] Hitoshi Kanoh and Nobuaki Nakamura, "Route Guidance with Unspecified Staging Posts Using Genetic Algorithm for Car Navigation Systems", in Proc. Intelligent Transportation Systems, 2000, pp. 119-124
[13] Yi-Liang Xu, Meng-Hiot Lim and Meng-Joo Er, "Investigation on Genetic Representations for Vehicle Routing Problem", in Systems, Man and Cybernetics, IEEE International Conference, 2005, pp. 3083-3088
[14] Mattiussi. C and Floreano. D., "Analog Genetic Encoding for the Evolution of Circuits and Networks", in Evolutionary Computation, IEEE Transactions, 2007, pp. 596-607
[15] Young-uk Chung and Dong-Ho Cho, "Enhanced softhandoff scheme for real-time streaming services in intelligent transportation systems based on CDMA", in Intelligent Transportation Systems, IEEE Transactions, 2006, pp. 147-155