ПСЕВДОГЕНЕТИЧЕСКИЙ АЛГОРИТМ ДЛЯ РЕШЕНИЯ ЗАДАЧИ ОПРЕДЕЛЕНИЯ ЛУЧШЕГО ПУТИ
Авторы: S. Behzadi, Ali A. Alesheikh
Перевод с английского: Казакова Ю. С.
Источник: http://isprsserv.ifp.uni-stuttgart.de/proceedings/XXXVII/congress/2_pdf/2_WG-II-2/15.pdf
КЛЮЧЕВЫЕ СЛОВА: генетический алгоритм, задача о кратчайшем пути, мутация, кроссинговер, псевдо ГА.

Аннотация

    В течение последних нескольких лет наблюдается экспоненциальный рост исследований, разработки и использования геоинформационных систем (ГИС). Не смотря на то, что ГИС были разработаны, чтобы бросить вызов большинству типов задач пространственного анализа, многие из более сложных пространственных задач все еще находятся вне их возможностей решения. Такого рода проблемы, часто сталкиваются с большим пространством поиска и большим количеством потенциальных решений. В таких случаях, стандартные аналитические методы, как правило, не могут найти оптимальные решения этой задачи в рамках практических временных и/или вычислительных ограничений. Одной из таких проблем в области пространственного анализа является задача маршрутизации. В данной статье основное внимание уделяется разработке алгоритмического решения задачи определения наилучшего пути. Поиск оптимального пути имеет много практических применений в области исследования операций, логистики, дистрибуции, управления цепочками поставок и транспортировки. В общем, определение лучшего пути состоит в нахождении эффективных маршрутов для путешественников по транспортной сети, в целях сведения к минимуму протяженности маршрута, стоимость услуг, времени, количества транспортных средств и т.д. Это задачи комбинаторной оптимизации, для которых не существует простых решений. В качестве альтернативного варианта реализованы и испытаны методы из области эволюционных вычислений для решения примера лучшего пути. Сфера эволюционных вычислений (ЭВ) развивалась для интеграции нескольких ранее исследованных связанных областей исследований в одну. Часть ЭВ включают генетические алгоритмы, эволюционное программирование, эволюционные стратегии и генетическое программирование. ЭВ используют вычислительные методы, аналогичные эволюционным механизмам, которые работают в рамках естественных биологических систем, таких как естественный отбор (например, выживание наиболее приспособленных), кроссинговер, мутацию и т.д. В рамках ЭВ, эти операторы используются в качестве средства быстро развития оптимального или близкого к оптимальному решения задачи при разработанной вычислительной основе представления соответствующего пространства поиска. Эта работа рассматривает, с научной точки зрения, эволюционные алгоритмы в решении задач геоинформационных систем. На основе их преимущества и недостатков методов разработан новый алгоритм, названный псевдо ГА. Алгоритм протестирован на различных исследованиях. Представлены результаты работы. Результаты анализа эффективности нового алгоритма является обнадеживающим.

1. ВВЕДЕНИЕ

    Генетические алгоритмы основываются на теории Дарвина об эволюции [3]. Генетические алгоритмы эволюционировали, развивались. Генетический алгоритм – метод для решения задачи оптимизации, который основан на естественном отборе, процессе, который управляет биологическим развитием. Генетический алгоритм неоднократно изменяет популяцию особей-решений. На каждом шаге генетического алгоритма случайным образом выбираются особи из текущей популяции в качестве родителей, и использует для производства потомков (следующего поколения). Последовательно от поколения к поколению популяция «развивается» к оптимальному решению. Алгоритм начинается с набора решений (представленного хромосомами), который называется популяцией. Решения одной популяции используются для формирования новой популяции. Это мотивировано надеждой, что новая совокупность будет лучше, чем старая. Решения, которые выбраны для создания новых решений (потомства) выбираются в зависимости от их пригодности – чем они более подходящие, тем больше у них шансов на участие в воспроизведении [4].
    Это повторяется, пока некоторые условия (например, количество населения или улучшение лучшего решения) не будут выполнены.
Ниже приводится краткая информация о том, как работает генетический алгоритм [2]:
  1. Алгоритм начинается с создания случайной начальной популяции.
  2. Затем алгоритм создает последовательность новых популяций, или поколений. На каждом шаге алгоритм использует особей в текущей популяции для создания следующего поколения. Для создания нового поколения, алгоритм выполняет следующие действия:
    1. Вычисление значения фитнесс-функции для каждой особи текущего поколения.
    2. Масштабирование значений фитнесс-функции для преобразования в более удобный диапазон значений.
    3. Выбор родителей, исходя из их пригодности.
    4. Производство потомков от родителей. Потомки генерируются либо путем случайного изменения одного родителя – мутации – либо путем сочетания элементов векторов пары родителей – кроссинговер.
    5. Замена текущего поколения потомками для формирования следующего поколения.
  3. Алгоритм продолжается, пока не будет выполнен один из критериев остановки.
    Генетический алгоритм отличается от стандартного алгоритма оптимизации двумя основными характеристиками, что показано в следующей таблице [2].

    Таблица 1. Сравнение стандартного алгоритма и генетического алгоритма
Стандартный алгоритм Генетический Алгоритм
Генерирует единственное значение на каждой итерации. Последовательность значений приближается к оптимальному решению. Генерирует совокупность значений на каждой итерации. Совокупность приближается к оптимальному решению.
Выбирает следующее значение в последовательности с помощью детерминированных вычислений. Выбирает следующую совокупность вычислениями, которые связаны со случайным выбором.

    В этой статье будут найдены кратчайшие пути от каждого каждому. При таком подходе все параметры генетического алгоритма будет описаны на основании правил стандартного алгоритма.

2. Реализация

2.1 Разработка

    Каждому городу в карте присвоен уникальный индекс, целочисленное значение от 1 … … … … N, где, N – число городов на карте. Каждая особь представляет решение задачи, при этом она не должна содержать повторные индексы городов. Длина особи выбрана равной числу городов на полной карте; следовательно могут быть варианты при которых самый кратчайший путь может содержать общее количество городов[1].
    Для карты с N количеством городов длина гена равна N, где Ti это i-й город на карте.
    [T1, T2… T (N-1), TN]

2.2 Кодирование

    В этой задаче используется кодирование перестановкой. В кодировании перестановкой каждая хромосома – строка чисел, которые представляют номер города в последовательности. Число городов в каждой хромосоме не одинаково [5].

2.3 Инициализация популяции

    В этой задаче нет определенного количества особей начальной популяции, и начальная популяция будет создана на основе критерия задачи.

2.4 Генерация особей начальной совокупности

    Начальная популяция создается на основе матрицы весов сети. Начальная популяция представляет собой набор отдельных особей с длиной равной двум. Первый ген каждой особи – это точечка-источник, а второй ген – пункт назначения.
    Если существует маршрут между i, j, генерируется особь [i, j]. Все особи первого поколения создаются таким образом. Особи генерируются на основе матрицы весов соединений между точками. Некоторые из этих особей показаны на рисунке 1.
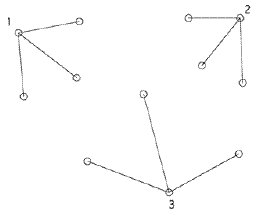
Рисунок 1. Некоторые особи первого поколения

2.5 Фитнесс-функция

    Фитнесс-функцией каждой особи в первом поколении является вес линии, связывающей два узла. Например, (i,j)=Cij это одна особь в первом поколении, ее длина составляет 2 и она представляет собой связь между i, j, и Cij – ее фитнес-функция.

2.6 Масштабирование значений фитнес-функции

    Масштабирование значений фитнес-функции преобразует исходные оценки пригодности, которые были возвращены фитнес-функцией, в значения в диапазоне, который подходит для функции выбора. Функция выбора использует масштабированное значение пригодности для выбора родителей для следующего поколения. Функция выбора присваивает высокую вероятность выбора особям, имеющим лучшее значение пригодности. После создания исходной популяции рассчитываются значения фитнесс-функции для каждой особи. В этом исследовании для определения масштабированных значений индивидуальных пропорциональных оценок пригодности особей используется пропорциональное масштабирование [2].

2.7 Оператор кроссинговера

    Оператор кроссинговера в этом методе отличается от используемых в настоящее время. Особи первого поколения сгенерированны по взвешенной матрице. Как правило, особи генерируются с помощью следующих уравнений:
Особи первого поколения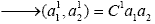
…
Особи (k-1)–го поколения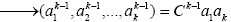
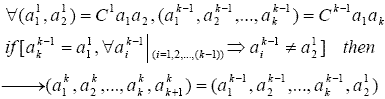    Особей первого и k-го поколений можно используются для создания особей при k-го поколения. Их комбинации представлены следующими уравнениями:
(1)
    В каждом поколении выбираются лучшие особи. Этот выбор представлен следующими уравнениями:
(2)
    Этот выбор представлен на рисунке 2.
Рисунок 2. Сравнение двух маршрутов в поколении

    Затем выбираются лучшие особи, которые имеет минимальный вес соединения, и имеют одинаковые начальные и конечные точки. Таким образом, определяется подходящая популяция в каждом поколении. Число особей в каждом поколении различно.
    Оператор кроссинговера может быть применен к особям текущего поколения и других поколений, ожидая следующее поколение.

2.8 Миграция

    Миграция определяет, как особи перемещаются между субпопуляциями. Если миграция происходит, лучшие особи из одной субпопуляции заменяют худшие особи в другой субпопуляции. Особи, которые мигрируют из одной в другую субпопуляцию, копируются. Они не удаляются из субпопуляции источника [2]. Процесс миграции этого подхода заключается в прямом и обратном направлении. Сначала, все особи в предыдущих поколениях переходят в текущее поколение (миграция вперед). Особи, которые выжили в предыдущем поколении – лучшие особи в своем поколении. Выполняется сравнение текущих особей и мигрировавших особей и лучшие особи выживают, а другие уничтожаются. Выжившая особь может содержаться в текущем поколение или в предыдущем поколении. Если особи, содержатся в предыдущем поколений, они возвращаются в свои поколения (обратная миграция). Сравнение между особями, представлено следующими уравнениями:
(3)
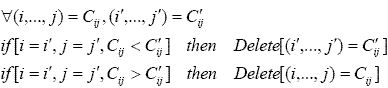    Сравнение показано на рисунке 3.
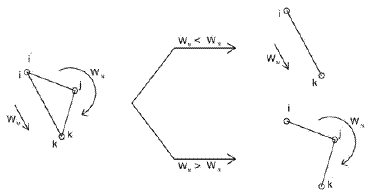
Рисунок 3. Сравнение двух поколений

    Если веса двух особей равны, они обе могут выжить или одна из них будет уничтожена по другим критериям, таким как прочие веса.
    В сети, которая имеет n узлов, существует (n -1) маршрутов к другим узлам из каждого узла, и будут созданы n(n -1) таких сетей, таким образом, общее число особей, в этой сети n(n - 1).

2.9 Критерии остановки

    В генетическом алгоритме существуют некоторые критерии остановки алгоритм, такие как число итераций [6], предельное число поколения, предельное время выполнения и т.д. Если выполняется один из этих критериев, алгоритм завершается.
    В предложенном новом алгоритме, существуют два критерия остановки:
  1. Если все особи в новом поколении уничтожены мигрировавшими особями, тогда нет особей для создания нового поколения, следовательно, алгоритм останавливается.
  2. Когда созданы особи с длиной n генов. Эти особи находятся в (n -1) поколении. В этом случае нет узла (гена) в области для присоединения к хромосоме, потому что все узлы включены в хромосому, следовательно, алгоритм останавливается.
    Если этот алгоритм используется для реальной сети, то, как правило, выполняется первый критерий остановки, так как редко бывает, что лучший путь проходит через все узлы.

3. Эксперименты

    Для оценки эффективности изложенного метода было проведено несколько экспериментов с использованием реальных дорожных карт частей Тегерана, столицы Ирана (рисунок 5). В этой задаче длины дуг рассматриваются в качестве весов этих дуг. Цель заключается в минимизации общей стоимости пути. Результат этого эксперимента показан на рис. 5.
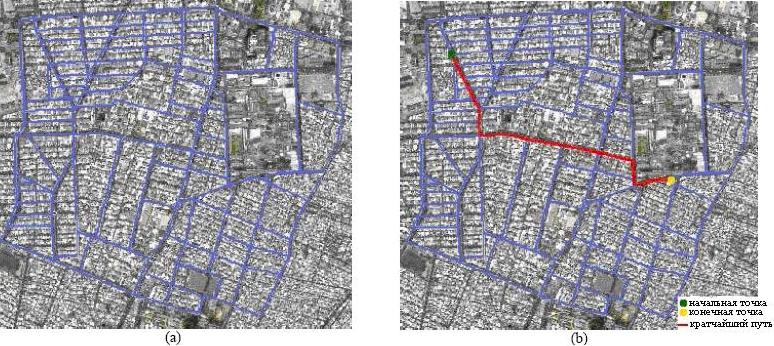
Рис.5. а. Часть тестовой карты           b. Начальная и Конечная точки и кратчайший путь

4. Выводы

    В этой статье был предложен новый метод поиска наилучшего пути. В этом методе все параметры генетического алгоритма были описаны на основе правил стандартного алгоритма. Используя этот метод, найдены кратчайшие пути от каждого узла к каждому узлу. При решении задачи определения кратчайшего пути использовались ГА. В этом алгоритме используются все параметры ГА, но использование параметров основано на детерминированных расчетах. Результат решения задачи определения лучшего пути показывает, что редко лучший путь проходит через все узлы, следовательно количество шагов этого алгоритма меньше, чем n, в отличии от алгоритма Дейкстры. данный алгоритм имеет высокую Гибкость и может быть использован для решения других проблем, таких как Задача коммивояжера (ЗК), определения ближайшего объекта, нахождение зоны обслуживания и т.д. скорость решения задачи может изменяться с помощью ряда условий, например изменения этого алгоритма на поиск пути от одного узла ко всем остальным.

5. Ссылки

[1] Abeysundara S., Giritharan B., Kodithuwakku S., 2005, A Genetic Algorithm Approach to Solve the Shortest Path Problem for Road Maps, Proceedings of the International Conference on Information and Automation, pp. 272-275.
[2] "Genetic Algorithm and Direct Search", http://www.mathworks.com/access/helpdesk/help/toolbox/gads/ (accessed 30 July. 2007)
[3] Hosseinali F., Alesheikh Ali A., 2008, Weighting Spatial Information in GIS for Copper Mining Exploration, American Journal of Applied Sciences. Vol. 5, No. 9, pp. 1187- 1198.
[4] "Introduction to Genetic Algorithms", http://cs.felk.cvut.cz/~xobitko/ga/ (accessed 7 Jun. 2007)
[5] Levitin G., Rubinovitz J., Shnits B., 2006, A genetic algorithm for robotic assembly line balancing, European Journal of Operational Research 168 (3) 811–825
[6] Yang H., Yang C., Gan L., 2006, Models and algorithms for the screen line-based traffic-counting location problems, Computers & Operations Research, 33, pp.836–858