В условиях рыночной экономики и активной конкуренции особую остроту приобретает проблема ускорения темпов автоматизация процессов проектирования и производства изделий. В связи с этим наблюдается быстрое развитие систем автоматизированного проектирования (САПР) в таких отраслях, как авиастроение, автомобилестроение, тяжелое машиностроение, архитектура и строительство, а также в производстве товаров народного потребления. При этом возможности существующих САПР не всегда удовлетворяют потребностям производства, а затраты на покупку лицензионного соглашения могут значительно превосходить полезный эффект от ее использования.
Поэтому часто на предприятиях принимается решение о создании собственной САПР с набором необходимых функциональных возможностей.  Разработка подобной системы с «нуля» весьма трудоемкий и длительный процесс. Построение иерархии базовых классов, написание функций для преобразования и отображения графических объектов, разработка основных инструментов для создания и редактирования объектов в интерактивном режиме может занять не одну неделю. Поэтому возникает потребность в некоторой библиотеке классов и функций, на базе которой можно было бы создать систему, решающую конкретные прикладные задачи.

Статья продолжает работу, начатую в [1-3]. Актуальность проблемы минимизации затрат на внедрение и разработку проблемно-ориентированных САПР рассмотрена в [4].  В [5] предложено разработать систему геометрического моделирования, поддерживающую связь между операциями над комплексным чертежом объекта и его трехмерным представлением.

Рассмотрим новые возможности системы, описанной в [1], выделим основные направления дальнейшего развития темы.

Возможности базовой системы были расширены за счет добавления операций, связывающих комплексный чертеж и 3d-сцену. Для этого в библиотеку введена функция Make3d, строящая трехмерную модель на основе двухмерного представления. Расширены возможности классов Line, Ellipse и Cycle, позволяющие создавать и редактировать объекты в интерактивном режиме. Реализованы классы Cone и Cylinder.
Система дает возможность по двум проекциям эллипса построить его трехмерное представление. При этом две выбранные проекции могут не соответствовать друг другу с точки зрения ортогонального проецирования. Система автоматически приведет их друг другу, минимизировав изменения исходных объектов. Пример решения такой задачи на рисунке 1.

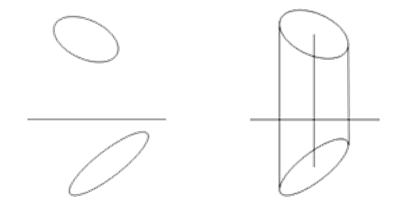
Рисунок 1 – Приведение проекций к соответствию

Основное условие для соответствия – любая точка на фронтальной проекции должна быть отражена на горизонтальную проекцию, и обратно.
Для совмещения проекций выбирается «главная», под которую будет преобразована вторая. В случаи двух эллипсов, достаточно совместить их центры по координате X и изменить длины полуосей так, чтобы их проекции на ось Х были равны. В случае, когда эллипс находится в проецирующем положении и одна из его проекций отрезок, появляется аналогичная подзадача, решаемая с учетом того, какой элемент был выбран «главным»,  отрезок или эллипс.
Решение основной задачи – построения 3d-модели эллипса сводится к нахождению натуральной величины осей эллипса, построению эллипса в начале координат, переносу и повороту.
Используя такие базовые объекты, как линия и эллипс в качестве геометрического определителя, можно задать некоторые поверхности вращения – конус и цилиндр.
Геометрическими определителями конуса является его основание и вершина. В системе реализована возможность построения конуса путем выделения проекций его определителей на чертеже. В 3d-сцене конус описывается каркасной моделью, где отображается кривая основания и четыре образующих боковой поверхности.
На рисунке 2 показано решение задачи нахождения сечения конуса.
Наглядности решения способствует опциональный режим отображения проекций конуса на плоскости проецирования.

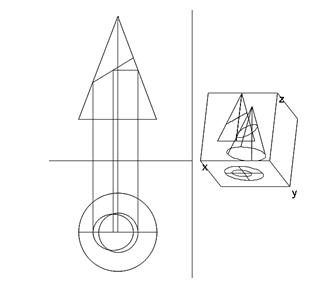
Рисунок 2 – Нахождение сечения конуса

Аналогично реализована операция отображения цилиндра в трехмерное пространство. Цилиндр задается основанием и точкой центра второго основания.

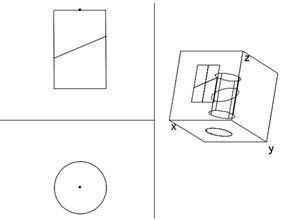
Рисунок 3 – Нахождение сечения цилиндра

Кроме того система дополнена операциями редактирования объектов: копирования и вставки

Реализованная система, доказывает работоспособность  базовой библиотеки классов и функций. Библиотека может быть использована как основа для ряда других продуктов нацеленных в частности на преобразования двумерных чертежей в трехмерную модель или в обучающих целях как наглядный инструмент построения и преобразования комплексного чертежа.
В будущем планируется расширить возможности библиотеки, добавить кривые произвольного вида, заменит каркасную модель на поверхностную.

1. Карабчевский В.В., Хлепитько И.В. Графический редактор для работы с параметризованными двухмерными объектами // Інформатика та комп'ютерні тенхнології - 2007 / Матеріали ІІІ науково-технічної конференції молодих учених та студентів. - Донецьк, ДонНТУ - 2007. - 550с.;іл., с. 278-280
2. Карабчевский В.В., Хлепитько И.В. Разработка проблемно-ориентированных систем геометрического моделирования // Наукові праці Донецького національного технічного університету. Серія «Проблеми моделювання та автоматизації проектування динамічних систем» (МАП-2007). Випуск: 6 (127) – Донецьк: ДонНТУ. – 2007. – С. 234–239
3. Карабчевський В.В., Хлепітько І.В. Засоби розробки систем геометричного моделювання // Наукові нотатки. Міжвузівський збірник (за напрямом «Інженерна механіка»). Випуск 22. Частина 1. «Сучасні проблеми геометричного моделювання (квітень, 2008). – Луцьк, 2008. – С.133-137.
4. Ширяев Н.Н. Пути минимизации затрат на внедрение PLM-решений на отечественных предприятиях [Электронный ресурс] / Ширяев Н.Н. – Режим доступа: http://www.sapr.ru/article.aspx
5. Карабчевський В.В. Засоби зв’язку між операціями над двовимірними і тривимірними моделями. // Наукові праці Донецького національного технічного університету. Серія Інформатика, кібернетика та обчислювальна техніка, випуск 93. Донецьк: ДонНТУ. – 2005. – С. 41-46.