Мы представляем интерфейс для создания и модификации 2-х и 3-х мерной геометрии на основе сплайнов. Пользователь в интерактивном режиме от руки рисует элементы на плоскости или на произвольной поверхности, и система автоматически восстанавливает вероятный результат, новую кривую или поверхность произвольной формы. Предлагается несколько интуитивно понятных операций над моделью, которые пользователь может выбрать в зависимости от своего опыта и предпочтений. Логические операции, непонятные для новичка, и схема модели сложной произвольной формы, сходные по мощности, предоставляются как альтернативные. Если кривая наносится на поверхность, она может изменяться без отрыва от этой поверхности. Предоставляются операции редактирования: масштабирование, перенос, поворот и т.д. Затем кривая может быт применена для создания (вырезания) отверстия в объекте и/или вытягивания «ручки» у объекта. Структура системы позволяет моделировать сложные объекты произвольной формы в интуитивно понятным режиме, избегая использования Логических операций.

Геометрические CAD системы уже давно стали стандартным инструментом в процессе проектирования. С годами они становятся очень мощным, но в то же время очень сложным оборудованием, поэтому часть рассматриваются как отдельная дисциплина. Дизайнеры, чаще всего инженеры, тратят много времени на изучение функциональных возможностей моделирующей системы и управления процессом моделирования. С точки зрения, как новичков, так и опытных пользователей, применения CAD систем — это непрактичное использование современных моделирующих технологий. Кроме того, современные CAD системы в большинстве своем разработаны для специализированных объектов и не поддерживают генерацию черновых набросков, которые создаются на концептуальном этапе проектирования.

Поскольку CAD системы не просты в понимании и не поддерживают ранние этапы проектирования, основная часть исследование просвещена разработке нового концептуального инструмента для моделирования набросков. Наверно самая первая компьютеризованная система для создания набросков (фактически самая первая CAD система) была Sutherland’s Sketchpad [14]. В этой системе пользователь использует световое перо для рисования на экране, и управляет такими графическими примитивами как арка и линия. После Sketchpad, было разработано большое количество пакетов рисования, но не многие из них нацелены на понимание рисуемой картинки, связь между элементами, соединение отдельных компонентов и формирования более широкого контекста однозначно определяется пользователем.

Это работа предлагает различные методы для моделирования сложной геометрии. Инструмент был разработан в надежде что новые и опытные пользователи найдут его простым и удобным в использовании. Пока большинство современных CAD системы используют логические операции для конструирования сложной геометрии из простой, мы утверждаем, что логические операции не понятны для непрофессиональных пользователей. Мы предлагаем альтернативную логическим операциям схему модели, которая обладает теме же возможностями, но по мнению авторов более интуитивно понятно для построения и редактирования сложных моделей.

Этот инструмент был разработан как расширение моделирующей системы GuIrit. Пакет GuIrit используется как пользовательский графический интерфейс в ядре твердотельного моделирования Irit. Результаты исследования реализованы как два новых расширения библиотеки системы GuIrit, наброски кривых и наброски поверхностей.

В прошлом были разработаны только две системы для моделирования набросков, которые обрабатывали движения пользователя, воспринимаемые как мазки кисти, и в интерактивном режиме создавали 3d геометрию. Большинство таких систем создает полигональную модель. А системы обработки набросков с геометрией произвольной формы менее распространены. Наша задача, разработать интерфейс для произвольных форм, с помощью которого можно будет легко создавать сложные модели и контролировать точность результатов построения.

Обычно построение новой геометрии начинают с примитивов: сфера или куб, и постепенно конструируют более сложные формы с использованием CSG операторов. Системы для построения набросков не исключение, например система ShapeShope. Она использует иерархическую объемную модель базирующуюся на примитивах типа куб и сфера и строит модель в интерактивном режиме с помощью CSG операторов. В противоположность этому, мы предлагаем управление геометрией напрямую, как более интуитивно понятную схему, в сравнении с булевскими операторами.

Еще один метод — это техника «выдувания» поверхностей, где полигональная сетка вытягивается из 2d чертежа контуров модели. Igarashi предложил систему под названием Teddy, которая позволяет рисовать примитивные модели произвольной формы с очень простым интерфейсом. Процедура требует чертеж контуров модели и затем строит под него полигональную сеть. Похожие результаты были представлены Карпенко в его системе SmoothSketch. Хотя метод очень прост в применении, он не универсален и может быть использован только для построения примитивных моделей округлой и выпуклой формы. Кроме того метод основанный на контурном представлении модели неточен и не может быть адаптирован для представления произвольных форм.

Некоторые системы используют наброски произвольной формы для создания 2d и 3d кривых. Приложение SKETCH — это интересная попытка создать инструмент для быстрого создания и редактирования аппроксимированных 3d сцен с использованием простого нереалистичного рендеринга. Интерфейс, построенный исключительно на жестах, базируется на рисовании примитивов с помощью линий, что позволяет все операции перенести в 3d пространство. Eggli et al предлагает 2d/3d инструмент для компьютеров, использующих для управления ручку. Пользователи такой системы определяют кривые, проводя пером по экрану ПК. Система может быть также использована для создания твердотельных 3d объектов и B-сплайновых поверхностей. Мы предлагаем интерфейс, позволяющий рисовать кривые от руки, используя не только плоские поверхности, но и любые поверхности общего положения и произвольной формы.

Еще один способ создания моделей произвольной формы — это использования деформации и разных преобразований над существующей геометрией. К примеру, Han, который предложил метод, сочетающий построение набросков от руки и ограниченные деформации для построения моделей произвольной формы.

На рынке доступно большое число систем и графических ядер 3d моделирования. Рассмотрим три инструмента для рисования от руки в популярных платных системах.

SketchUp (http://sketchup.google.com/): Google SketchUp это инструмент, который позволяет не профессиональным пользователям легко создавать и редактировать 3d модели. Хотя, результирующая модель полиномиальная и весьма упрошенная. Он базируется на операции вытягивании плоского полигона в 3-х мерную форму. Последняя версия SketchUp позволяет также создавать фигуры вращения и заметания. Доступен также инструмент для рисования линий, позволяющий создавать и редактировать кривые с помощью точек, лежащих на них. Точки могут быть добавлены к кривой или удалены с нее, могут менять ее форму, путем их перетягивания в ручную.

SolidWorks (http://www.solidworks.com/): SolidWorks может создавать от руки 2d кривые с помощью сплайнов и аналитической геометрии, например линии, арки и конические сечения. Он может провести кривую через три точки отмеченные в пространстве или присоединенные к существующей модели. Но он не может обеспечить гладксоть или непрерывность кривой на концах. Он также может построть 3d кривую используя так называемый 3d-набросок. Этот тип набросков позволяет определить кривую на плоскости или на 3d поверхности с помощью набора точек, с условием что кривая будет принадлежать поверхности. Никакого свободного редактирования кривой на поверхности в этом случае нет. SolidWorks может создавать поверхности заметания с несколькими образующими.

Rhino (http://www.rhino3d.com/): Rhino позваляет создавать 2-х мерные и 3-х мерные кривые , используя точки, через которые она проходит, точки которые ее интерполируют ривуются от руки. Рисование на поверхности позволяет рисовать только на одной поверхности. пользователь должен выбрать на какой поверхности он будет рисовать: на полигональной сетке или NURBS поверхности. Проецирование кривой позволено только для плоских поверхностей и оно всегда перпендикулярно плоскости проецирования. Результирующая проекция кривой для ее дальнейшего использования должна быть переопределена, командой «перестроить».

Все это говорит о том, что современным системам моделирования не достает инструментов для построения набросков. Сложная геометрия по прежнему строится с помощью логических операций, нет возможностей построить кривую на произвольных поверхностях, проецирование кривых ограничено, а создание поверхностей заметания малофункционально и не интуитивно в использовании.

Эта работа предлагает систему для интуитивно понятного геометрического моделирования сложных моделей произвольной формы. Она дает возможность, как опытным пользователям, так и новичкам строить сложные модели с заданной точностью. В этой технологии не используются логические операции, в интерактивном режиме создается B-spline кривая или поверхность, которые затем могут быть отредактированы с помощью интуитивного жестового интерфейса.

Данные из наброска конвертируются в B-spline произвольной формы с контрольными точками заданными виде вектора R⁵ (x,y,z,u,v). Где (x,y,z) – координаты точки в прямоугольной системе координат, (u,v) — параметры определяющие кривую относительно ниже лежащей поверхности. Если кривая наносится на поверхность заданную параметрически: S(u, v) = (Sx(u, v), Sy(u, v), Sz(u, v)), то (u,v) параметры задаются для каждой точки устройством ввода и считаются достоверными. Покрывая ниже лежащую поверхность, кривая может быть представлена как набор точек Sx(u, v), Sy(u, v), Sz(u, v)).

В общем случае, пространственная прямая, точки которой лежат на поверхности S, не принадлежит поверхности S полностью. Это справедливо не только для обычных B-сплайнов, а также для линейных B-сплайнов. Это значит, что если взять ломанную, построенную вдоль кривой, точки перелома которой принадлежат поверхности S, не все ее точки будут принадлежать этой поверхности. Возьмем C(t) = (u(t), v(t)). Тогда композицию S(C(t)) — истинное отражение (u(t), v(t)) на S. К сожалению вычисление такого выражения требует значительных временных затрат и выражение имеет большую степень (степень выражения равна суммарной степени C и S). Если взять С, как (u(t), v(t)), можно избежать вычисления выражения явно, и вычислить S(C(t)) в каждой точке с наперед заданной точностью.

Операция рисования кривой не ограничена одной ниже лежащей поверхностью. Одна непрерывная линия может принадлежать нескольким поверхностям и проходить через все заданные положения, позволяя пользователю чередовать процесс рисования с процессом изменения сцены. Так как процесс автоматического определения поверхности проходит во время рисования кривой, для каждой точки кривой, запоминается изменения поверхности.

Создание кривой на поверхности не точно по свей сути. Хотя рисование кривой на прямую имеет свои преимущества, должны быть разработаны формы с большей точностью построения. Рассмотрим цилиндр из которого пользователь собирается «вытянуть» другую цилиндрическую форму, в направлении перпендикулярном оси исходного цилиндра. Чтобы облегчить этот процесс мы предлагаем метод более точный чем тот, который реализован в большинстве CAD систем. Произвольные плоские или пространственные прямые могут быть спроецированы на произвольную поверхность вдоль заданного направления V. Каждая точка кривой отражается на поверхность S вдоль направляющего луча V. При этом луч может вообще не проходить через поверхность или «пробивать» ее в нескольких местах. Кроме того, две смежных точки кривой могут быть разорваны при проецировании. Все эти случаи должны быть выявлены путем тщательного исследования мест пересечения V и S.

Проекция может быть рассмотрена как пересечение поверхностей, в данном случаи S поверхности и поверхности, полученной путем выдавливания кривой C вдоль направляющего луча V, R(t, r) = C(t) + Vr, r ≥ 0. В этом случаи результат аппроксимируется ломаной линией.

Рисунок 1 — Левый рисунок показывает кривую нанесенную на несколько поверхностей, при чередовании процесса рисования кривой и изменения сцены. Правый рисунок показывает проецирования группы кривых на цилиндр.

Если кривая создана на поверхности, пользователю может понадобится отредактировать ее или переместить. В [7] множество схем редактирования были адоптированы для прямой трансформации кривых на поверхности. Мы так же предлагаем адаптировать идею прямого редактирования кривых, но для трансформации. Процесс переноса, вращения, и/или масштабирования объекта на плоскости или в пространстве весьма прост и интуитивен. Мы адаптировали этот процесс, чтобы позволить трансформацию кривых нанесенных на поверхность произвольной формы.

Рассмотрим поверхность S(u,v). Предположим, что над S осуществляется изометрия. В этом случае расстояние между точками S сохраняется. Тогда трансформацию T можно применить к (u(t), v(t)) как T(u(t), v(t)). Выражение S(T(u(t), v(t))) обеспечит обратную связь с новым положением кривой C на поверхности S.

К сожалению в большинстве случаев преобразование поверхности S не сохраняет расстояния между точками, поэтому возникает необходимость аппроксимировать кривую с учетом трансформаций S. Возьмем точку (u0, v0), центральную точку кривой C (например центра тяжести), принадлежащую параметрической области поверхности S. Вычислив Якобиан поверхности S в точке (u0, v0) можно аппроксимировать кривую с учетом T преобразования. Если S неразрывна, Якобиан может быть определен в любой ее точки, а значит можно найти положение любой точки кривой C на трансформированной поверхности.

Чтобы сделать операцию трансформации наглядной и интуитивно понятной, выбранная кривая заключается в трансформационный фрейм. Фрейм представляет собой набор дополнительных кривых заданных в параметрической области поверхности S и образующих ограничивающий прямоугольник для кривой С. Этот фрейм предлагает узлы для поворота, переноса и масштабирования кривой вручную, путем клика по ним мышью.

Рисунок 2 — Кривая С (черного цвета) на поверхности S (желтого цвета) выбрана для трансформации. Фрейм трансформации окружает кривую с узлами по углам (зеленые кружки) для поворота и на границах (красные квадратики) для растяжения. Операция масштабирования осуществляется с помощью зеленных кружков при зажатой клавише Shift.

Имея кривую заданную на плоскости и в пространстве, покрывающую некоторую поверхность, мы готовы к заданию с ее помощью новых поверхностей.

Общее представление поверхностей в современных средах моделирования представляет собой тензорное произведение поверхностей. Урезанные поверхности часто используются, чтобы обойти ограничение прямоугольной топологии тензорного произведения. Результаты Булевских операций, в большинстве случаев, предоставляются как ряд урезанных поверхностей, попарно сложенных (вычтенных). Прямая манипуляция над урезанными поверхностями конечно выполнима, но, как мы уже указали, Булевские операции мало понятны для неопытных пользователей, поэтому идея вырезать/наращивать поверхность вдоль произвольной кривой легка для восприятия. Следовательно, мы действительно позволяем конечным пользователям урезать поверхности вдоль кривой наложенной на поверхность. В результате никаких топологических ограничений не накладывается на геометрию модели.

Операция вырезания или вытягивания поверхности вдоль кривой может быть проделана только если кривая замкнута. Если же кривая разомкнута, т.е ее начало и конец не совпадают, пользователь не может использовать ее для создании новой поверхности, пока не соединит ее концы.

Чтобы получить поверхность E путем выдавливания, нужно взять кривую C на поверхности, направляющий вектор V и создать новую поверхность путем выдавливания кривой C вдоль направляющего вектора V E(t, r) = C(t) + Vr. Вспомните кривую которую мы спроецировали на цилиндр. Эта кривая может теперь быть вытеснена в пространство вдоль V, чтобы создать новое цилиндрическое тело. Другими словами, мы создали сочетание двух цилиндров без участия логических операций.

Таким же путем новая поверхность м.б. создана при протягивании кривой вдоль заданного пути. Конструктор для создания поверхностей путем заметания также легок в использовании и интуитивно понятен. Выделяя кривую на поверхности C, пользователь должен определить другую кривую А, вдоль которой будет протянута кривая С. Рисунок 3 показывает пример протягивания кривой принадлежащей поверхности вдоль другой кривой.

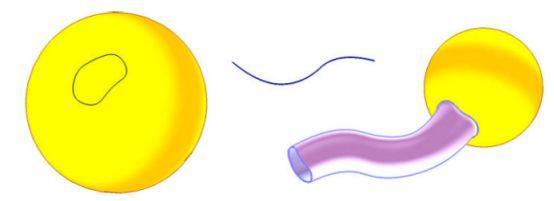
Рисунок 3 — Создание поверхности путем протягивания кривой C нанесенной на поверхность S (желтого цвета) вдоль пути заданного кривой А (синего цвета).

Созданная поверхность С0 будет соединена с поверхностью S через кривую С. Поскольку во многих случаях требуется сгладить этот переход, необходимо сделать следующее рядом с C(t) = (u(t), v(t)). Пусть 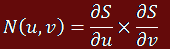— нормальное векторное поле поверхности S(u,v).  Тогда векторное поле вдоль кривой С будет иметь вид

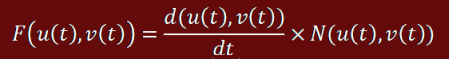
F(u, v) определена в касательном пространстве поверхности S для всех точек принадлежащих кривой С. Тогда новая кривая определяется как D(u,v) = C(u,v) + F(u,v). D — вторая секция новой поверхности заметания. Поскольку перекрестная производная первого порядка для новой поверхности определена в области F, то результирующая поверхность и поверхность S в области кривой C будут плавно соединены.

Рисунок 4 — Пример плавного соединения двух поверхностей в области кривой С

Однако не всегда необходимо состыковывать старую поверхность S с новой поверхностью заметания. Возможно поверхность S только вспомогательная. Для этого случая предусмотрена возможность выбора для пользователя, где строить поверхность заметания. Направляющая кривая может быть состыкована с центром кривой C или же центр кривой С может быть перенесен в начало направляющей кривой, тогда новая поверхность будет отделена от поверхности S. После создания новой поверхности, она предоставляется пользователю в режиме редактирования. Вдоль поверхности располагаются области редактирования для каждой из секций. Пользователь может выбрать одну из секций и применить к ней различные трансформации для изменения результирующей поверхности заметания. К секции можно применить операции переноса, масштабирования и поворота, можно даже заменить кривую на  совершенно другую. Можно также перевести секцию в полигональную модель.

Рисунок 5 — Каждая секция поверхности заметания из рисунка 3 редактируема с помощью контроллера управления изображенного с права. С лева показан возможный результат изменений поверхности посекционно

В нашем исследовании мы разработали и адоптировали технику построения трехмерных поверхностей и кривых. Мы представили интуитивно понятные инструменты моделирования, с помощью которых неопытные дизайнеры могут создавать и редактировать сложные формы.

Не каждая модель произвольной формы может быть создана с помощью представленных инструментов или же сделана с легкостью. Например, представьте, что вам нужно сделать отверстие на каждой кнопке клавиатуры. Создание этих отверстий по одному может быть весьма утомительным, автоматическое размножение отверстий по поверхности весьма облегчило бы этот процесс. Операция симметричного отображения также могла бы облегчить конструирование, например для создания ног или ручек. Кроме того возможно стоит добавить более понятные инструменты редактирования, которые облегчили бы процесс моделирования.

1. Banks, M.; Cohen, E.: Real Time Spline Curves from Interactively Sketched Data, Symposium on Interactive 3D Graphics, 1990, 99-107.
2. Cohen, E.; Riesenfeld, R. F.; Elber, G.: Geometric Modeling with Splines: An Introduction, AK Peters, 2001.
3. Conner, D. B.; Snibbe, S. S.; Herndon, K. P.; Robbins, D. C.; Zeleznik, R. C.; Van Dam, A.: Three dimensional widgets, proceedings of the 1992 symposium on Interactive 3D graphics, Cambridge, Massachusetts, United States, 1992, 183 – 188.
4. Do Carmo, M.: Differential Geometry of Curves and Surfaces, Prentice-Hall, 1976.
5. Eggli, L.; Hsu, C. Y.; Bruderlin, B. D.; Elber, G.: Inferring 3D Models from Freehand Sketches and Constraints, Computer-Aided Design, 29(2), 1997, 101-112.
6. Elber, G.: Free Form Surface Analysis using a Hybrid of Symbolic and Numeric Computation, Ph.D. Thesis, University of Utah, Computer Science Department, 1992.
7. Elber, G.: Multiresolution Curve Editing with Linear Constraints, The Journal of Computing & Information Science in Engineering, 1(4), 2001, 347-355.
8. Elber, G.: Symbolic and Numeric Computation in Curve Interrogation, Computer Graphics forum, 14(1), 1995, 25-34.
9. Han, L.; Amicis, R.; Conti, G.: Interactive Spline-Driven Deformation for Free-Form Surface Styling, Symposium on Solid and Physical Modeling, 2006, 139-147.
10. Igarashi, T.; Matsuoka, S.; Tanaka, H.: Teddy: A Sketching Interface for 3D Freeform Design, SIGGRAPH, 1999, 409-416.
11. Karpenko, O.; Hughes, J.; Raskar, R.: SmoothSketch: 3D Free-Form Shapes from Complex Sketches, ACM Trans. Graph, 25(3), 2006, 589-598.
12. Kim, K.; Elber, G.: New Approaches to Freeform Surface Fillets, The Journal of Visualization and Computer Animation, 8(2), 1997, 69-80.
13. Kazinnik, R.; Elber, G.: Orthogonal Decomposition of Non-Uniform Bspline Spaces using Wavelets, Computer Graphics Forum, 16(3), 1997, 27-38.
14. Sutherland, I.: A Man-Mashine Graphical Communication System, Ph.D. Thesis, MIT, Boston, Massachusetts, 1963.