Повышение оперативности, эффективности, точности выполнения проектных процедур конструкторско-технологической подготовки производства (КТПП) — одна из важнейших задач, стоящих сегодня перед российской промышленностью. Это связано прежде всего со структурой спроса в машиностроении: чаще всего требуется мелкосерийное производство с жесткими сроками выполнения заказа. Сокращение сроков выполнения можно добиваться двумя основными путями: ускорением КТПП и ускорением собственно производственного процесса. При этом второй способ существенно ограничен физическими свойствами объектов и предметов производства, задающих некоторые предельные значения производительности технологического оборудования. Поэтому наибольшие резервы скрыты именно в сокращении сроков подготовки производства, для чего на предприятиях внедряются разнообразные системы автоматизации труда конструктора и технолога (CAD/CAM/CAE-системы).

Обобщение производственного опыта ряда машиностроительных предприятий позволяет сделать вывод о применимости методов геометрического моделирования к решению широкого ряда задач автоматизации КТПП, среди которых — параметрическое проектирование конструктивно однородных изделий, динамическое моделирование работы изделия, материальное нормирование, разработка и верификация управляющих программ и другие процедуры, связанные с анализом и преобразованием информации о геометрии детали, заготовки и инструмента. Будем называть такие процедуры геометрическими (рис. 1).

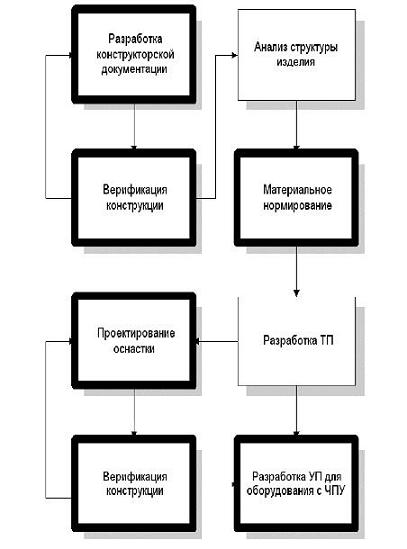
Рисунок 1 — Применение геометрического моделирования (выделено рамкой) в проектных процедурах КТПП

В настоящее время для автоматизации геометрических процедур используются в целом принципиально различные по своему построению системы, в каждой из которых реализованы достаточно сложные алгоритмы обработки информации. Например, параметрическое проектирование выполняется в универсальной САПР типа SolidWorks, Pro/E или T-Flex, материальное нор- мирование — при помощи отдельного самостоятельного разработанного модуля (отметим, данная проектная процедура редко автоматизируется даже в мощных интегрированных пакетах автоматизации всего предприятия, таких, как CA-PRMS), анализ кинематики делается при помощи одной из "тяжелых" САПР, управляющие программы разрабатываются еще одним внешним моду- лем и т.д.

Предлагается использовать новый универсальный подход к выполнению процедур КТПП, заключающийся в применении единой методологии их выполнения, являющейся чисто геометрической. Предлагаемая методология основа на следующих соображениях.

1. В большинстве современных САПР имеется встроенное геометрическое ядро 3D-моделирования (например, ANSYS или ParaSolid), в котором корректно реализованы сложные алгоритмы описания и обработки трехмерных объектов.
2. Возможна тождественная замена аналитической расчетной модели той или иной проектной процедуры на определенное геометрическое преобразование, реализуемое при помощи встроенных алгоритмов САПР. Подобный подход заменяет сложную расчетную модель (рис. 2, а) на гораздо более простое преобразование информации для ее последующей обработки алгоритмами 3D-ядра (рис. 2, б).

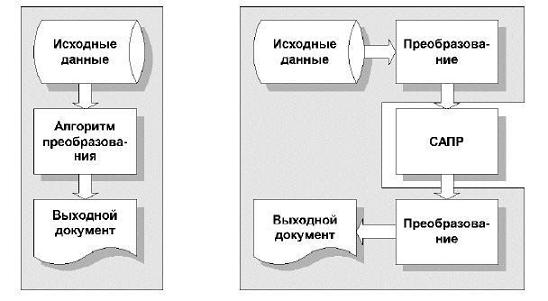
Рисунок 2 — Традиционный (а) и предлагаемый (б) подходы к выполнению геометрических проектных процедур

Под геометрическим моделированием будем понимать прежде всего создание виртуальной модели реального объекта, сохраняющей такие его свойства, как форма и взаимное расположение ограничивающих объект элементов. В предлагаемой концепции размеры ограничивающих элементов не являются составной частью самой модели, а рассматриваются как внешние параметры.

Тогда геометрическая модель объекта есть совокупность

       (1)

где : L — вектор описаний ограничивающих элементов; P — вектор описания графа смежности объекта.

Способ задания отдельных элементов вектора L может быть различным. Это и канонические уравнения прямых, окружностей, поверхностей, и таблично-интерполяционное задание геометрии, и набор R-функций [1].

Модель (1) описывает некоторое множество реальных объектов, имеющих одинаковые наборы ограничивающих элементов и одинаковый граф смежности, но разные наборы размерных параметров. С технологической точки зрения речь идет о группе конструктивно подобных деталей со сходной технологией изготовления.

Для выделения из модели конкретного варианта конструкции введем понятие функции визуализации [2] :

,      (2)

где: P₀ — вектор привязки, задающий положение всей модели в пространстве; S — вектор размерных параметров.

Функция (2) выполняет восстановление модели путем решения систем уравнений, содержащихся в L и получения константных координат всех ограничивающих элементов.

Введем ряд базовых операций над моделями, реализация которых позволяет решать задачи автоматизации проектных процедур КТПП. Проведенный анализ показал, что необходимым и достаточным является следующий набор операций:

1. Модификация вектора S (параметрическое проектирование).
2. Модификация вектора P₀ (кинематическое моделирование, компоновка конструкторских гра- фических документов)
3. Выполнение булевских операций пересечения и вычитания над моделями М₁ и М₂ с образованием новой модели М₃:

M₃ = M₁ ∩ M₂         (3.1)

M₃ = M₁ − M₂        (3.2)

Геометрическое ядро современных САПР обеспечивает выполнение всех этих операций, поскольку базовые алгоритмы таких преобразований хорошо известны.

Рассмотрим теперь укрупненную схему проектных процедур КТПП (рис. 1) с точки зрения применимости геометрического моделирования для их выполнения и покажем применение трех перечисленных операций в задачах автоматизации этих процедур.

В большинстве случаев конструктор выполняет заимствование и модификацию ранее созданного проектного решения, что заметно повышает производительность труда. Особенно заметно это проявляется при проектировании оснастки, когда число возможных вариантов конструкции ограничено имеющимся на предприятии парком технологического оборудования. Если представить вектор S ! как точку в n-мерном фазовом пространстве множества вариантов модели M_f (n равно числу компонентов вектора S), то можно показать, что процесс поиска оптимального проектного решения есть последовательный перебор ряда точек из M_f до достижения требуемых геометрических характеристик модели. Оценка характеристик выполняется экспертом-конструктором путем сравнения текущего результата выполнения функции (2) с имеющимся заданием на проектирование. Следует отметить, что траектория в пространстве M_f в общем случае является разрывной, а конфигурация пространства M_f накладывает ограничения на модель, отсекающие заведомо невозможные конструкции. По достижении оптимального варианта конструктор выполняет компоновку графического документа путем изменения вектора P₀. Компоновка не связана с собственно проектированием, но является необходимым этапом оформления конструкторской документации.

Таким образом, для автоматизации проектирования класса изделий достаточно разработать функцию (2), наложить ограничения на ее фазовое пространство и реализовать интерфейс с конструктором — итерационный цикл ввода параметров, визуализации, оценки и компоновки. В рассматриваемой модели проектная процедура разработки конструкторской документации выражается системой:

     (4)

Применение геометрического моделирования наиболее важно именно в задачах верификации, так как во многих случаях единственной альтернативой является изготовление и испытания прототипа, что в условиях вариантного производства с быстро сменяющейся программой выпуска заведомо экономически невыгодно. Наибольшей трудностью отличается кинематическое моделирование механизмов машин, заключающееся в расчете траекторий перемещения деталей, в том числе деталей переменной формы (например, пружин). Расчет кинематики в рассматриваемом случае сводится к заданию положения внешнего объекта с некоторым шагом (определяющим точность моделирования) и определению моментов касания деталей механизма с объектом и друг с другом. Для определения момента касания воспользуемся операцией (3.1), которая продуцирует модель M₃ , являющуюся областью пересечения двух других моделей M₁ и M₂. Если изменять значения компонент векторов P₀¹ и P₀² по критерию:

V(M₃ = M₁ ∩ M₂) → 0,     (5)

где V — функция, возвращающая объем (для 3D-модели) или площадь (для 2D-модели) модели M₃, то можно с любой заданной точностью определить момент касания. Упругая сила пружин учитывается при выборе изменяемых компонент векторов P₀¹ и P₀² с учетом условия выбирания люфтов в механизме и, при необходимости, с учетом распределения силы, перемещающей внешний объект, по упругим элементам механизма.

Использование алгоритма перебора половинными делениями с откатом позволяет добиться высокой эффективности системы моделирования (так, реализованная авторами система моделирования клещевого захвата автоматической роторной линии [3] выполняет генерацию кадров положения деталей механизма с шагом в 1⁰ и с точностью 0,01мм за время Тм = 8…12 *Тp , где Tp - время работы реального механизма). Проектная процедура кинематической верификации конструкции выражается системой:

    (6)

Подобный чисто геометрический подход к кинематическому моделированию позволяет отказаться от крайне трудоемких расчетов траекторий и, самое главное, от изготовления опытного образца.

В данной проектной процедуре, помимо прочего, решается задача оптимизации размещения детали на заготовках из таких профилей, как лист, лента, полоса в той степени, в которой это позволяет присутствующая на данном этапе подготовки производства неопределенность, вызванная отсутствием разработанного технологического процесса. Окончательная оптимизация, приводящая к генерации сменных или суточных карт раскроя, является задачей диспетчирования, выполняемой непосредственно в ходе производства.

И предварительная, и окончательная оптимизация размещения — типичные для геометрического моделирования задачи. Подходы к их решению сходны с кинематическим моделированием: модифицируется вектор P₀ⁱ i-й размещаемой детали с соблюдением условия непересечения с уже размещенными деталями, что может быть выражено через условие (5). Для устранения вышеупомянутой неопределенности представляется целесообразным замена проекций деталей на описанные около них прямоугольники, что резко сокращает дерево перебора вариантов и позволяет найти оптимальное решение за приемлемое время [4]. Условием размещения будет:

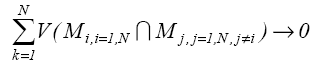     (7)

где N — число размещаемых деталей. Несмотря на то, что в общем случае такой подход приведет к некоторому завышению материальных норм, он гарантирует выполнение производственного задания даже в случае отсутствия дальнейшей оптимизации. Мера риска невыполнения производственного задания явно превосходит меру риска закупки излишнего количества материалов.

На протяжении ряда лет коллективом кафедры «Автоматизированные станочные системы» Тульского государственного университета были реализованы и внедрены в промышленность (ОАО «Тяжпромарматура», г. Алексин; ОАО «Тульский патронный завод», г. Тула; НПО «Комплекс», г. Тверь и др.) системы автоматизации КТПП, основанные на изложенных принципах. В качестве геометрического ядра используется система AutoCAD14 и 2000 благодаря ее широкой распространенности, подготовленности персонала промышленных предприятий и наличию развитых средств программирования. На базе AutoCAD удалось реализовать системы параметрического проектирования [6], автоматической параметризации чертежей [7], кинематического моделирования [8], оптимизации листового раскроя [9], моделирования и оптимизации 3-х координатной фрезерной обработки. Ведется работа по дальнейшему совершенствованию этих систем и их взаимной интеграции.

Итак, предлагаемая схема геометрического моделирования позволяет использовать унифицированный подход при автоматизации ряда разнообразных проектных процедур КТПП. Как отмечалось выше, в современных САПР реализованы эффективные алгоритмы выполнения операций над геометрическими моделями, поэтому основное внимание следует уделять вопросу оптимального использования существующих средств в производственной практике. Дальнейшие исследования направлены на автоматизацию создания параметрической модели по имеющемуся проекционному чертежу, автоматическую классификацию геометрических моделей и чертежей по конструктивно-технологическим признакам, использование подхода, известного как feature-based design [10, с.3-6] при генерации техпроцессов и УП для ЧПУ.

1. Куценко Л.Н., Маркин Л.В. Формы и формулы. - М.: Изд-во МАИ, 1994. 176с.: ил.
2. . Гришин С.А., Гельфонд М.В., Троицкий Д.И. Автоматизированная генерация функций отображения в САПР // Тезисы докладов VII всероссийской конференции по компьютерной геометрии и графике КОГРАФ-97. - Нижний Новгород, НГТУ, 1997 - с. 123 Иноземцев А.Н., Троицкий Д.И. /Прикладная геометрия, вып.3, N 4 (2001), стр. 57 – 66
3. Гельфонд М.В., Григорьева Н.С., Троицкий Д.И. Автоматизация проектирования захватных органов технологического оборудования // Современные проблемы информатизации в технике и технологиях: Труды V Международной электронной научной конференции. - Воронеж: ЦЧКИ, 2000 - с.110
4. Анцев В.Ю., Иноземцев А.Н., Троицкий Д.И. Материальное нормирование на базе интегри рованной компьютеризированной системы // Техника машиностроения, №4(22), 1999, с.33-37
5. Mikell P. Groover, Emory W. Zimmers, Jr. Computer-Aided Design and Manufacturing. Prentice Hall, Inc., New Jersey, 1984.
6. Bannatyne M.W.McK., Inozemtsev A.N., Troitsky D.I. Parametric Modeling: Concept and Implementation // Proceedings of the IEEE International Conference on Information Visualization. July 19-21, 2000, London, England. pp. 504-509
7. Афонин С.А., Григорьева Н.С., Троицкий Д.И. Решение задачи параметризации чертежей // Известия Тульского государственного университета. Серия "Машиностроение". Выпуск 6 (специальный). Сборник избранных трудов конференции "Автоматизация и информатизация в машиностроении 2000" (АИМ 2000). - Тула: ТулГУ, 2000. - 288с. С. 171-178
8. Гельфонд М.В., Григорьева Н.С., Троицкий Д.И. Автоматизация проектирования захватных органов технологического оборудования // Современные проблемы информатизации в технике и технологиях: Труды V Международной электронной научной конференции. - Воронеж: ЦЧКИ, 2000 - с.110
9. Григорьева Н.С., Троицкий Д.И. Информационные технологии в задачах раскроя листовых материалов // Перспективные технологии автоматизации. Тезисы докладов международной электронной научно-технической конференции // Вологда, 1999. - с.12
10. Richard F. Ferraro. A Tutorial Guide to PT/Modeler 2.0™ and Pro/ENGINEER. Addison-Wesley, 1998.