Boosting – Усиление простых классификаторов

Усиление простых классификаторов – подход к решению задачи классификации (распознавания), путём комбинирования примитивных <слабых> классификаторов в один <сильный>. Под <силой> классификатора в данном случае подразумевается эффективность (качество) решения задачи классификации. В данной статье речь пойдёт о семействе алгоритмов, в основе которых лежит алгоритм AdaBoost (от английских слов <адаптивность> и <усиление>) описанный в 1996 Freund и Schapire [1]. Этот алгоритм был успешно использован во многих областях, в частности для задачи поиска лиц на изображении [5]. Подход усиления простых классификаторов применяется во многих задачах и до сих пор является объектом множества, как прикладных, так и теоретических исследований.

В основе метода усиления простых классификаторов лежит простая предпосылка: скомбинировать некоторое количество элементарных (простых) признаков, таким образом, чтобы получить один, но более мощный. Приведём классический пример: пускай человек, играющий на скачках, решил создать программу, которая бы предсказывала, придёт ли интересующая его лошадь первой к финишу. Опросив некоторое количество играющих людей, он смог определить несколько эмпирических правил: ставь на лошадь, которая победила в трёх предыдущих заездах, ставь на лошадь, ставки на которую максимальны и т.д. Ясно, что каждое из таких правил по отдельности недостаточно надёжно и встает вопрос можно ли их оптимально скомбинировать для получения надёжных результатов. Ответ на этот вопрос даёт семейство алгоритмов работающих на принципе усиления простых классификаторов. Это семейство использует простые правила классификации подобно деталям конструктора, комбинируя их неким образом, чтобы в итоге получить более сильное правило.

AdaBoost

Мы рассмотрим один из самых ранних алгоритмов из данного семейства – AdaBoost (от <адаптивность> и <усиление>). Этот алгоритм был опубликован в 1996 и послужил основой для всех последующих исследований в данной области. На его основе была построена на данный момент пожалуй самая эффективная (как по уровню распознавания, так и по скорости работы) система поиска объектов на изображении (Viola-Jones Object Detector [5]). На данный момент наиболее распространёнными вариантами базового алгоритма являются Gentle AdaBoost и Real AdaBoost, превосходящие базовый алгоритм по своим характеристикам, но сохраняют все основные принципы. К основным достоинствам AdaBoost и его вариантов можно отнести высокую скорость работы, высокую эффективность распознавания, простоту реализации, общность.

Описание алгоритма
Требуется построить классифицирующую функцию , где X - пространство векторов признаков, Y - пространство меток классов. Пусть в нашем распоряжении имеется обучающая выборка (x₁, y₁), ..., (x_N, y_N). Где вектор признаков, а метка класса, к которому принадлежит . Далее в статье мы будем рассматривать задачу с двумя классами, то есть Y = {-1; +1}. Также у нас есть семейство простых классифицирующий функций . Мы будем строить финальный классификатор в следующей форме: , где . Построим итеративный процесс, где на каждом шаге будем добавлять новое слагаемое , вычисляя его с учётом работы уже построенной части классификатора. На каждом шаге будем для каждого примера (x_i, y_i) из обучающей выборки вычислять его «вес»: положим D₀(i) = 1 / N, тогда где Zi - нормализующий коэффициент, такой что Вес каждого элемента обучающей выборки на текущем шаге задает <важность> этого примера для очередного шага обучения алгоритма. Чем больше вес, тем больше алгоритм будет <стараться> на данном шаге классифицировать этот пример правильно. Как видно из формулы, чем уверенней пример распознаётся предыдущими шагами, тем его вес меньше - таким образом, самые большие веса получают примеры, которые предыдущими шагами были классифицированы неверно. Проще говоря, мы варьируем веса таким образом, чтобы классификатор, включенный в комитет на текущем шаге, <концентрировался> на примерах, с которыми предыдущие шагами <не справились>. Таким образом на каждом шаге мы работаем с какой-то частью данных, плохо классифицируемой предыдущими шагами, а в итоге комбинируем все промежуточные результаты. Очередной простой классификатор мы будем выбирать исходя из взвешенной с распределением D_m ошибки. Мы выбираем (тренируем) минимизирующий взвешенную ошибку классификации Заметим, что если рассмотреть D_m как распределение вероятности над X, что правомерно т.к. , то Далее вычисляется вклад текущего слагаемого классифицирующей функции В этом разделе мы уделим внимание фундаменту всех методов усиления простых классификаторов - семейству простых классификаторов Что это такое? Для ясности приведём пример: пусть входные данные это n-мерные вектора X = Rⁿ, пусть тогда , то есть это порог по k-той координате. Такой классификатор в англоязычной литературе носит имя «пень» (stump) - основа дерева.

Как при таком множестве H происходит выбор наилучшего классификатора h^{Θ, k} на каждой итерации (шаг алгоритма 2.a)? В данном случае делается следующее - для каждого k = 1..n, вычисляется порог Θ'_k, реализующий минимум взвешенной ошибки e_m, затем из полученных классификаторов h^{Θ, k}, k = 1..n выбирается соответствующий минимальной e_m.

Несмотря на свою простоту, этот классификатор, усиленный алгоритмом AdaBoost, дает весьма впечатляющие результаты. Система поиска объектов на изображении Viola-Jones находит 95% всех искомых объектов и с 0.0001% ложных срабатываний. Какими свойствами должен обладать простой классификатор? В первую очередь, вероятность его ошибки должна быть хотя бы немного меньше 1/2, то есть он должен работать лучше чем «орел/решка»: Так же, простой классификатор должен быть максимально простой структуры (обладать малой VC-размерностью [11]) - это связано с оценкой ошибки обобщения сильного классификатора; более подробную информация можно найти здесь [1][3][4].
Самыми часто используемыми на практике простыми классификаторами являются пороги (stumps) и CART решающие деревья [12], [13].

Внутренняя механика AdaBoost
В этой части мы попытаемся пролить немного света на внутреннюю механику алгоритма. Фактически, AdaBoost осуществляет два действия:

• - Отбор простых классификаторов (простых признаков)
• - Комбинирование отобранных классификаторов

Первое действие является своеобразным отображением пространства входных векторов в пространство значений простых классификаторов:

Комбинирование простых классификаторов происходит линейно (составляется линейная комбинация), а решение принимается в зависимости от знака полученной комбинации. Это фактически эквивалентно разделению пространства значений простых классификаторов гиперплоскостью и принятие решения в зависимости от того, по какую сторону гиперплоскости лежит отображение вектора признаков.
Таким образом, готовый классификатор производит вначале отображение в некое пространство, обычно намного более высокой размерности, чем исходное, в котором производит линейную классификацию. На этапе тренировки алгоритм последовательно строит и это отображение, и саму гиперплоскость.
Стоит заметить, что работа AdaBoost в значительной мере напоминает работу алгоритма ядерной машины опорных векторов (Kernel Support Vector Machine - kernel SVM). Исследования последних лет показывает глубокую связь этих двух алгоритмов, что является серьёзным теоретическим результатом [9].
Одна из интерпретаций работы алгоритмов на основе AdaBoost основана на понятие <грани> (margin). В случае AdaBoost грань определяется как: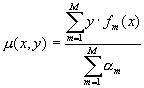

Эту величину можно интерпретировать как меру <уверенности> классификатора в примере (x, y). Если классификация правильная, то грань больше нуля, иначе грань отрицательна. Чем больше простых классификаторов правильно классифицируют пример, тем больше его грань.
Если учесть то, как на каждом шаге вычисляются веса примеров, то легко видеть, что на каждом шаге AdaBoost пытается максимизировать минимальную грань тренировочной выборки. Утверждается, что данное действие положительно сказывается на обобщающих способностях алгоритма. Больше про данную интерпретацию семейства алгоритмов на основе AdaBoost можно прочитать в [9].

Заключение

В данный момент подход усиления простых классификаторов является одним из наиболее популярных и, вероятно, наиболее эффективным методом классификации. За счёт высокой скорости, простоты реализации и высокой эффективности распознавания это семейство алгоритмов нашло свое применение во множестве областей так или иначе связанных с классификацией (медицина, анализ изображений, анализ текстов и т.д.).

Список литературы

[1] Yoav Freund and Robert E. Schapire. A Short Introduction to Boosting. Journal of Japanese Society for Artificial Intelligence, 14(5):771-780, September, 1999.

[2] Jerome Friedman, Trevor Hastie, and Robert Tibshirani. Additive logistic regression: A statistical view of boosting. The Annals of Statistics, 38(2):337-374, April 2000.

[3] Y Freund and R. E. Schapire. Game theory, on-line prediction and boosting. In Proceedings of the Ninth Annual Conference on Computational Learning Theory, pages 325-332, 1996.

[4] R. E. Schapire. The Boosting Approach to Machine Learning. An Overview.MSRI Workshop on Nonlinear Estimation and Classification, 2002.

[5] R. Lienhart, A. Kuranov, V. Pisarevsky. Empirical Analysis of Detection Cascades of Boosted Classifiers for Rapid Object Detection. MRL Technical Report, 2002.

[6] Pavlov, D. Mao, J. Dom, B. Scaling-up Support Vector Machines Using Boosting Algorithm. Proceedings. 15th International Conference on Pattern Recognition, 2000.

[7] P. Viola and M. Jones. Robust Real-time Object Detection. In Proc. 2nd Int'l Workshop on Statistical and Computational Theories of Vision -- Modeling, Learning, Computing and Sampling, Vancouver, Canada, July 2001.

[8] T. G. Dietterich. Machine Learning Research: Four Current Directions AI Magazine. 18 (4), 97-136, 1997.

[9] Rosset, Zhu and Hastie. Boosting as a Regularized Path to a Maximum Margin Classifier. Journal of Machine Learning Research 5 (2004) 941-973, 2004.

[10] Y Freund and R. E. Schapire. A decision-theoretic generalization of on-line learning and an application to boosting. Journal of Computer and System Sciences, 55(1):119-139,August 1997.

[11] Метод опорных векторов, Цифровая библиотека лаборатории компьютерной графики и мультимедиа ВМиК МГУ, http://library.graphicon.ru/catalog/217.

[12] Classification and Regression Trees (C&RT), Electronic Textbook by StatSoft, http://www.statsoft.com/textbook/stcart.html.

[13] Деревья классификации, Электронный учебник StatSoft, http://www.statsoft.ru/home/textbook/modules/stclatre.html.