Maximilian Riesenhuber and Tomaso Poggio
Nat Neurosci 1999, 2:1019-1025.
Department of Brain and Cognitive Sciences, McGovern Institute for Brain Research, Center for Biological and Computational Learning and Artificial Intelligence Laboratory, Massachusetts Institute of Technology, Cambridge, Massachusetts 02142, USA
Correspondence should be addressed to T.P. (tp@ai.mit.edu)
Understanding how biological visual systems recognize objects is one of the ultimate goals in computational neuroscience. From the computational viewpoint of learning, different recognition tasks, such as categorization and identification, are similar, representing different trade-offs between specificity and invariance. Thus, the different tasks do not require different classes of models. We briefly review some recent trends in computational vision and then focus on feedforward, view-based models that are supported by psychophysical and physiological data.
Imagine waiting for incoming passengers at the arrival gate at the airport. Your visual system can easily find faces and identify whether one of them is your friend’s. As with other tasks that our brain does effortlessly, visual recognition has turned out to be difficult for computers. In its general form, it is a very difficult computational problem, which is likely to be significantly involved in eventually making intelligent machines. Not surprisingly, it is also an open and key problem for neuroscience.
The main computational difficult y is the problem of variability. A vision system needs to generalize across huge variations in the appearance of an object such as a face, due for instance to viewpoint, illumination or occlusions. At the same time, the system needs to maintain specificity. It is important here to note that an object can be recognized at a variety of levels of specificity: a cat can be recognized as “my cat” on the individual level, or more broadly on the categorical level as “cat”, “mammal”, “animal” and so forth.
Within recognition, we can distinguish two main tasks: identification and categorization. Which of the two tasks is easier and which comes first? The answers from neuroscience and computer vision are strikingly different. Typically, computer vision techniques achieve identification relatively easily, as shown by the several companies selling face identification systems, and categorization with much more difficulty. For biological visual systems, however, categorization is suggested to be simpler1. In any case, it has been common in the past few years, especially in visual neuropsychology, to assume that different strategies are required for these different recognition tasks2. Here we take the computational view3,4 that identification and categorization, rather than being two distinct tasks, represent two points in a spectrum of generalization levels.
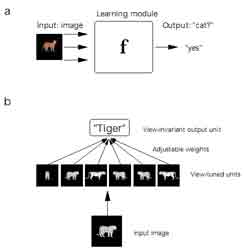
Much of the interesting recent computational work in object recognition considers the recognition problem as a supervised learning problem. We start with a very simplified description (Fig. 1a). The learning module’s input is an image, its output is a label, for either the class of the object in the image (is it a cat?) or its individual identity (is it my friend’s face?). For simplicity, we describe a learning module as a binary classifier that gives an output of either “yes” or “no.” The learning module is trained with a set of examples, which are a set of input–output pairs, that is, images previously labeled. Positive and negative examples are usually needed.
In this setting, the distinction between identification and categorization is mostly semantic. In the case of categorization, the range of possible variations seems larger, because the system must generalize not only across different viewing conditions but also across different exemplars of the class (such as different types of dogs). The difficulty of the task, however, does not depend on identification versus categorization but on parameters such as the size and composition of the training set and how much of the variability required for generalization is covered by the training examples. For instance, the simple system described earlier could not identify an individual face from any viewpoint if trained with only a single view of that face. Conversely, the same system may easily categorize, for instance, dog images versus cat images if trained with a large set of examples covering the relevant variability.
Within this learning framework, the key issue is the type of invariance and whether it can in principle be obtained with just one example view. Clearly, the effects of two-dimensional (2D) affine transformations, which consist of combinations of scaling, translation, shearing and rotation in the image plane, can be estimated exactly from just one object view. Generic mechanisms, independent of specific objects and object class es, can be added to the learning system to provide invariance to these transformations. There is no need then to collect examples of one object or object class at all positions in the image to be able to generalize across positions from a single view. To determine the behavior of a specific object under transformations that depend on its 3D shape, such as illumination changes or rotation in depth, however, one view is generally not sufficient. In categorization, invariance also occurs across members of the class. Thus multiple example views are also needed to capture the appearance of multiple objects. Unlike affine 2D transformations, 3D rotations, as well as illumination changes and shape variations within a class, usually require multiple example views during learning. We believe that this distinction along types of invariance is more fundamental that the distinction between categorization and recognition, providing motivation for experiments to dissect the neural mechanisms of object recognition.
In computer vision applications, the learning module of Fig. 1a has been implemented in various ways. In one simple approach (Fig. 1b), each unit stores one of the example views and measures the similarity of the input image with the stored dictionary, that is, representations that are very compact because any given signal can be represented as the combination of a small number of features. Mallat makes the point by analogy: a complete representation is like a small English dictionary of just a few thousand words. Any concept can be described using the vocabular y but at the expense of long sentences. With a very large dictionary— say 100,000 words—concepts can be described with much shorter sentences, sometimes with a single word. In a similar way, overcomplete dictionaries of visual features allow for compac t re presentations. Sing le neurons in the macaque posterior inferotemporal cortex may be tuned to such a dictionary of thousands of complex shapes.
Newer algor ithms add a hierarchical approach in which non-overlapping12,13 or overlapping compo nents8,14 are first detected and then combined to represent a full view. As we discuss below, in models for object recog nition in the br ain, hier archies ar ise natur ally because of the need to obtain both specificity and invariance of position and scale in a biologically plausible way.
The performance of these computer vision algorithms is now very impressive in tasks such as detecting faces, people and cars in real-world images8,13. In addition, there is convincing evidence from computer vision15 that faces—and other objects—can be reliably detected in a view-invariant fashion over 180° of rotation in depth by combining just three detectors (Fig. 1b), one trained with and tuned to frontal faces, one to left profiles, and one to right profiles.

Fig. 1. Learning module schematics. (a) The general learning module. (b) A specific learning module: a classifier, trained to respond in a view-invariant manner to a certain object.
All these computer v ision schemes lack a natural implementation in terms of plausible neural mechanisms. Some of the basic ideas, however, are relevant for biological models.
More elaborate schemes have been developed, especially for the problem of object categorization in complex real-world scenes. They focus on classifying an image region for a particular viewpoint and then combine classifiers trained on different viewpoints. The main difference between the approaches lies in the features with which the examples are represented. Typically, a set of n measurements or filters are applied to the image, resulting in an n-dimensional feature vector. Various measures have been proposed as features, from the raw pixel values themselves6–8 to overcomplete measurements (see below), such as the ones obtained through a set of overcomplete wavelet filters9. Wavelets can be regarded as localized Fourier filters, with the shape of the simplest two-dimensional wavelets being suggestive of receptive fields in primary visual cortex.
The use of overcomplete dictionaries of features is an interesting new trend in signal processing10. Instead of representing a signal in terms of a traditional complete representation, such as Fourier components, one uses a redundant basis, such as the combination of several complete bases. It is then possible to find sparse representations of a given signal in this large example. The weighted outputs of all units are then added. If the sum is above a threshold, then the system’s output is 1; otherwise it is 0. During learning, weights and threshold are adjusted to optimize correct classification of examples. One of the earliest versions of this scheme was a model5 for identification of an individual object irrespective of viewpoint. Note that this approach is feedforward and view-based in the sense that there is no 3D model of the object that is mentally rotated for recognition, but rather novel views are recognized by interpolation between (a small number of ) stored views (Fig 1b).
View-based models have also been proposed to explain object recognition in cortex. As described above, in this class of models, objects are represented as collections of view-specific features, leading to recognition performance that is a function of previously seen object views, in contrast to so-called ‘objectcentered’ or ‘structural description’ models, which propose that objects are represented as descriptions of spatial arrangements among parts in a three-dimensional coordinate system that is centered on the object itself16. One of the most promi nent models of this type is the ‘recognition by components’ (RBC) theory17,18, in which the recognition process consists of extracting a view-invariant structural description of the object in terms of spatial relationships among volumetric primitives, ‘geons’, that is then matched to stored object descriptions. RBC predicts that recognition of objects should be viewpoint-invariant as long as the same structural description can be extracted from the different object views.
The question of whether the visual system uses a view-based or an object-centered representation has been the subject of mu ch con t rovers y 19,20 (for re v i ews, see refs. 2, 21). Ps y chophysical22,23 and physiological data24,25 support a viewbased approach, and we will not discuss these data further here. In this paper, we focus on view-based models of object recognition and show how they provide a common framework for identification and categorization.
Based on physiological experiments in monkeys2,11, object recognition in cortex is thought to be mediated by the ventral visual pathway26 from primar y visual cortex, V1, through extrastriate visual areas V2 and V4 to inferotemporal cortex, IT (Fig. 2). Neuropsychological and fMRI studies point to a crucial role of inferotemporal cortex for object recognition also in human vision2,26. As one proceeds along the ventral stream, neurons seem to show increasing receptive field sizes, along with a preference for increasingly complex stimuli27. Whereas neurons in V1 have small receptive fields and respond to simple bar-like stimuli, cells in IT show large receptive fields and prefer complex stimuli such as faces2,11,25. Tuning properties of IT cells seem to be shaped by task lear ning24,28,29. For instance, after monkeys were trained to discriminate between individual and highly similar ‘paperclip’ stimuli composed of bar segments24, neurons in IT were found that were tightly shape-tuned to the training objects. The great majority of these neurons responded only to a single view of the object, with a much smaller number responding to a single object-invariant viewpoint. In addition to this punctate representation, more distributed representations are likely also used in IT. Studies of ‘face cells’ (that is, neurons responding preferentially to faces) in IT argue for a distributed representation of this object class with the identity of a face being jointly encoded by the activation pattern over a group of face neurons30,31. Interestingly, view-tuned face cells are much more prevalent than viewinvariant face cells25. In either case, the activation of neurons in IT can then serve as input to higher cortical areas such as prefrontal cortex, a brain region central for the control of complex behavior32.
A zoo of view-based models of object recognition in cortex exists in the literature. Two major groups of models can be discerned based on whether they use a purely feedforward model of processing or use feedback connections. A first question to be asked of all models is how they deal with the 2D affine transformations described earlier. Although scale and position invariance can be achieved very easily in computer vision systems by serial scanning approaches, in which the whole image is searched for the object of interest sequentially at different positions and scales, such a strategy seems unlikely to be realized in neural hardware.
Feedback models include architectures that perform recognition by an analysis-by-synthesis approach: the system makes a guess about what object may be in the image and its position and scale, synthesizes a neural representation of it relying on stored memories, measures the difference between the hallucination and the actual visual input and proceeds to correct the initial
hypothesis3,33,34. Other models use top-down control to ‘renormalize’ the input image in position and scale before attempting to match it to a database of stored objects35,36, or conversely to tune the recognition system depending on the object’s transformed state, for instance by matching filter size to object size37.
Interestingly, EEG studies38 show that the human visual system can solve an object detection task within 150 ms, which is on the order of the latency of viewand object-tuned cells in inferotemporal cortex25. This does not rule out the use of feedback processing but strongly constrains its role in perceptual recognition based on similarity of visual appearance.
Indeed, this speed of processing is compatible with a class of view-based models that rely only on feedforward processing, similar to the computer vision algorithms described above. However, in these models, image-based invariances are not achieved by an unbiological scanning operation but rather are gradually built up in a hierarchy of units of increasing receptive field size and feature complexit y, as found in the vent r al
visual stream. One of the earliest representatives of this class of models is the ‘Neocognitron’39, a hierarchical network in which feature complexity and translation invariance are alternatingly increased in different layers of a processing hierarchy. Feature complexity is increased by a ‘template match’ operation in which higher-level neurons only fire if their afferents show a particular activation pattern; invariance is increased by pooling over units tuned to the same feature but at different positions. The concept of pooling units tuned to transformed versions of the same feature or object was subsequently proposed40 to explain invariance also to non-affine transformations, such as to rotation in depth or illumination changes, in agreement with the shorter latency of view-tuned cells relative to view-invariant cells observed experimentally25. Indeed, a biologically plausible model5 had motivated physiological experiments24, showing that view-invariant recognition of an object was possible by interpolating between a small number of stored views of that object.
The strategy of using different computational mechanisms to attain the twin goals of invariance and specificity has been used successfully in later models, among them the SEEMORE system41 and the HMAX model42. The latter, using a new pooling operation, demonstrated how scale and translation invariance could be achieved in view-tuned cells by a hierarchical model, in quantitative agreement with experimental IT neuron data24.
Two features are key to the success of hierarchical models39,42,43. First, the gradual and parallel increase of feature complexity and receptive field size, as found in the visual system, is crucial in avoiding a combinatorial explosion of the number of units in the system on one hand or insufficient discriminatory ability on the other hand. Although the invariance range is low at lower levels, thus requiring many cells to cover the required range of scales and positions, only a small set of simple features must be represented. Conversely, in higher layers, where neurons are tuned to a greater number of more complex features, neurons show a greater degree of invariance, thus requiring fewer cells tuned to the same feature at different positions and scales44. Second, in hierarchical models, a redundant set of more complex features in higher levels of the system is built from simpler features. These complex features are tolerant to local deformations as a result of the invariance properties of their afferents39,42,43. In this respect, they are related to (so far non-biological) recognition architectures based on feature trees that emphasize compositionality45. The end result is an overcomplete dictionary similar to the computer vision approaches reviewed earlier.
We propose a model (Fig. 3) that extends several existing mod els5,39,40,42,43. A view-based module, whose final stage consists of units tuned to specific views of specific objects, takes care of the invariance to image-based transformations. This module, of which HMAX42 is a specific example, probably comprises neurons from primary visual cortex (V1) up to, for instance, posterior IT (PIT). At higher stages such as in anterior IT, invariance to object-based transformations, such as rotation in depth, illumination and so forth, is achieved by pooling together the appropriate view-tuned cells for each object. Note that view-tuned models5 predict the existence of view-tuned as well as view-invariant units, whereas structural description models strictly predict only the latter. Finally, categorization and identification tasks, up to the motor response, are performed by circuits, possibly in prefrontal cortex (D.J. Freedman et al., Soc. Neurosci. Abstr., 25, 355.8, 1999), receiving inputs from object-specific and view-invariant cells. Without relevant view-invariant units, such as when the subject has only experienced an object from a certain viewpoint, as in the experiments on paperclip recognition22,24,46, task units could receive direct input from the view-tuned units (Fig. 3, dashed lines).

Fig. 2. The ventral visual stream of the macaque (modified from ref. 26).
Fig. 3. A class of models of object recognition. This sketch combines and extends several recent models5,39,40,42,43. On top of a view-based module, view-tuned model units (Vn) show tight tuning to rotation in depth (and illumination, and other object-dependent transformations such as facial expression and so forth) but are tolerant to scaling and translation of their preferred object view. Note that the cells labeled here as view-tuned units may be tuned to full or partial views, that is, connected to only a few of the feature units activated by the object view44. All the units in the model represent single cells modeled as simplified neurons with modifiable synapses. Invariance, for instance to rotation in depth, can then be increased by combining in a learning module several viewtuned units tuned to different views of the same object5, creating view-invariant units (On). These, as well as the view-tuned units, can then serve as input to task modules performing visual tasks such as identification/discrimination or object categorization. They can be the same generic learning modules (Fig. 1) but trained to perform different tasks. The stages up to the object-centered units probably encompass V1 to anterior IT (AIT). The last stage of task-dependent modules may be located in the prefrontal cortex (PFC).
In general, a particular object, say a specific face, will elicit different activity in the object-specific On cells of Fig. 3 tuned to a small nu mber of ‘pro to t y pical’ faces, as obser ved experimentally31. Thus, the memory of the particular face is represented in the identification circuit implicitly by a popu-
lation code through the activation pattern over the coarsely tuned On cells, without dedicated ‘grandmother’ cells. Discrimination, or memorization of specific objects, can then proceed by compar ing activation patter ns over the st rong ly activated objector view-tuned units. For a certain level of specificity, only the activations of a small number of units have to be stored, forming a sparse code—in contrast to activation patterns on lower levels, where units are less specific and hence activation patterns tend to involve more neurons. Computational studies in our laboratory47 provide evidence for the feasibility of such a representation. An interesting and non-trivial conjecture (supported by several experiments47–49) of this
population-based representation is that it should be able to generalize from a single view of a new object belonging to a class of objects sharing a common 3D structure—such as a specific face—to other views. Generalization is expected to be better than for other object classes in which members of the same class can have very different 3D structure, such as the ‘paperclip’ objects46. Similarly to identification, a categorization module (say, for dogs versus cats) uses as inputs the activities of a number of cells tuned to various animals, with weights set during learning so that the unit responds differently to animals from different classes50.
This simple framework illustrates how the same learning algorithm and architecture can support a variety of object recognition tasks such as categorization and identification (for a related proposal, see ref. 4). It can easily be extended to include inputs to task units from lower-level feature units and even other task units, with interesting implications for the learning of object class hierarchies or phenomena such as categorical perception50. The model can successfully perform recognition tasks such as identification47 and categorization50, with performance similar to human psychophysics47 and in qualitative agreement with monkey physiology (D.J. Freedman et al., Soc. Neurosci. Abstr., 25, 355.8, 1999).
Several predictions for physiology follow from this proposed architecture (Fig. 3). For instance, objects sharing a similar 3D structure, such as faces, would be expected to be represented in terms of a sparse population code, as activity in a small group of cells tuned to prototypes of the class. Objects that do not belong to such a class (paperclips) should need to be represented for unique identification in terms of a more punctate representation, similar to a look-up table and requiring, in the extreme limit, the activity of a single ‘grandmother’ cell. Further, identification and categorization circuits should receive signals from the same or equivalent cells tuned to specific objects or prototypes.
Here we have taken the view that basic recognition processes occur in a bottom-up way; it is, however, very likely that topdown signals are essential in controlling the learning phase of recognition51 and in some attentional effects, for instance in detection tasks, to bias recognition toward features of interest, as suggested by physiological studies52–55. The massive descending projections in the visual cortex are an obvious candidate for an anatomical substrate for top-down processing. One of the main challenges for future models is to integrate such topdown influences with bottom-up processing.
We can learn to recognize a specific object (such as a new face) immediately after a brief exposure. In the model we described in Fig. 3, only the last stages need to change their synaptic connections over a fast time scale. Cur rent psychophysical, physiological and fMRI evidence, however, suggests that learning takes place throughout the cortex from V1 to IT and beyond. A challenge lies in finding a learning scheme that describes how visual experience drives the development of features at lower levels, while assuring that features of the same type are pooled over in an appropriate fashion by the pooling units. Schemes for learning overcomplete representations have been proposed56, with extensions to the learning of invariances57. It remains to be seen whether a hierarchical version of such a scheme to construct an increasingly complex set of features is also feasible. Learning at all levels has been studied in a model of object recognition capable of recognizing simple configurations of bars, and even faces independent of position43, by exploiting temporal associations during the learning period58. In one proposal14 (see also refs. 13, 59), features are learned through the selection of significant components common to different examples of a class of objects. It would be interesting to translate the main aspects of this approach into a biologically plausible circuit.