В. Соловьев
Структурные модели конечных автоматов при их реализации на ПЛИС
Конечный автомат представляет собой наиболее общую математическую модель цифрового устройства или цифровой системы. Поэтому очень важно при разработке различных цифровых устройств и систем применять эффективные методы синтеза конечных автоматов. В то же время, реализованные в известных пакетах автоматизированного проектирования (фирм Altera, Xilinx и других) методы синтеза основаны на традиционных подходах, которые не позволяют эффективно использовать архитектурные возможности новой элементной базы.Данная статья является первой из серии статей, посвящённых новому подходу к синтезу конечных автоматов на ПЛИС. В рамках данной серии предполагается опубликовать следующие статьи: "Проектирование конечных автоматов на ПЛИС со структурой двух программируемых матриц"; "Использование выходных макроячеек ПЛИС в качестве элементов памяти конечных автоматов"; "Использование входных буферов ПЛИС в качестве элементов памяти конечных автоматов"; "Синтез на ПЛИС совмещённых моделей конечных автоматов"; "Верификация результатов синтеза конечных автоматов на ПЛИС"; "Пакет ZUBR автоматизированного проектирования конечных автоматов на ПЛИС".В статьях данной серии будут рассмотрены формальные методы синтеза конечных автоматов на ПЛИС, которые позволяют наиболее полно и эффективно использовать архитектурные возможности ПЛИС. Отличительной чертой всех методов синтеза является простота, что делает возможным их применение даже при ручном проектировании.Экспериментальные исследования показали, что предлагаемый подход позволяет сократить стоимость реализации и повысить быстродействие конечных автоматов, в среднем, в 2–3 раза, по сравнению с известными пакетами.
В настоящее время хорошо исследованы две модели автоматов: автомат Мили [1] и автомат Мура [2]. Известна также модель автомата [3,4], в которой наборы выходных сигналов совпадают с кодами внутренних состояний автомата. В отдельных работах предлагается использовать регистры на входах и выходах автомата для буферизации входных сигналов и согласования выходных сигналов с сигналами синхронизации [5].
Однако до сих пор не исследованы все возможные модели конечных автоматов, допускающих реализацию на современных программируемых логиче-ских интегральных схемах (ПЛИС), влияние установки регистров на входах и выходах на поведение автомата, во-просы временного согласования сигналов автоматов при передаче значений между различными уровнями в многоуровневых цифровых системах с различными способами обработки данных, не определена сложность реализации на ПЛИС различных моделей конечных автоматов и др. Указанные проблемы становятся особенно острыми, когда необходимо достичь максимального быстродействия устройства, приближающегося к предельной частоте функционирования ПЛИС.
В данной работе рассматриваются различные структурные модели конечных автоматов, допускающие реализацию на ПЛИС. Для этого вводятся различные классы конечных автоматов, на основании которых определяются структурные модели конечных автоматов, реализуемых на ПЛИС. Основной целью исследования является выявление свойств каждой модели с точки зрения быстродействия и стоимости реализации.
Классы конечных автоматов
На практике наибольшее распространение получили два типа конечных автоматов: автомат Мили и автомат Мура. Поведение автомата Мили описывается с помощью следующих уравнений:
at+1 =(zt,at); (1)
wt =(zt,at);
здесь функция переходов ![]() определяет следующее внутреннее состояние автомата
(состояние перехода) at+1, а функция выходов
определяет следующее внутреннее состояние автомата
(состояние перехода) at+1, а функция выходов - формируемый выходной
набор wt. Характерным для автомата Мили является то, что
выходной набор wt зависит как от входного набора zt, так и от внутреннего
состояния at
В автомате Мура функция выходов зависит только от состояния at и не зависит от входного набора, поэтому поведение автомата Мура описывается следующими уравнениями:
at+1 =(zt,at); (2)
wt =(at).
При построении конечных автоматов функции переходов ![]() и выходов
и выходов реализуются с
помощью комбинационных схем CL
![]() и CL
и CL,
соответственно, а память автомата реализуется в виде регистра RG, где в
каждый момент автоматного времени t~ хранится код внутреннего состояния
at. Структурные схемы автоматов Мили и Мура показаны на рис.
1а и 1б, соответственно. Особенностью структуры автомата Мура является
то, что комбинационная схема CLy, реализующая выходные функции, не имеет
непосредственной связи со входами схемы.
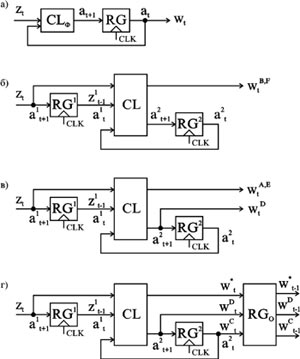
Рисунок 1. Основные структуры конечных автоматов: а - Мили класса A; б - Мура класса B; в - Мура класса С; г - Мили класса D; д - Мили класса E; е - Мура класса F;
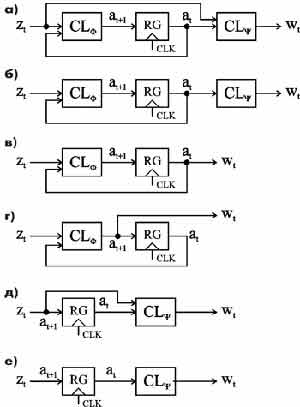
Если каждый выходной набор wt автомата Мура совпадает с кодом его внутреннего состояния at, то поведение автомата можно описать следующим образом:
~at+1 =(zt,at); (3)
wt = at.
Данный тип автомата называют автоматом класса C [6], аналогично,
автоматы Мили (рис.
1а) и Мура (рис.
1б) называют автоматами классов A и B, соответственно. Структура
автомата Мура класса C показана на рис.
1в. Её особенностью является отсутствие комбинационной схемы
CL, а также то, что все выходы автомата являются
регистровыми, поскольку формируются на выходах регистра RG. Отметим, что
данная структура легко реализуется на ПЛИС, поскольку все регистровые
выходы имеют цепи обратной связи с комбинационной частью ПЛИС.
Если каждый выходной набор wt автомата Мили совпадает с кодом его состояния перехода at+1, то имеем автомат класса D [7], поведение которого описывается следующими уравнениями:
~ at+1 =(zt,at); (4)
wt = at+1.
Структура автомата Мили класса D показана на рис.
1г. Её особенностью также является отсутствие комбинационной схемы
CL, однако выходы автомата являются комбинационными,
поскольку формируются на выходах комбинационной схемы CL
![]() .
Отметим, что необходимым условием реализации автоматов класса D на ПЛИС
является возможность такого конфигурирования выходных макроячеек, при
котором триггеры выходных макроячеек включены в цепи обратных связей.
.
Отметим, что необходимым условием реализации автоматов класса D на ПЛИС
является возможность такого конфигурирования выходных макроячеек, при
котором триггеры выходных макроячеек включены в цепи обратных связей.
Различие между автоматами классов C и D заключается в том, что в автомате класса C выходной набор wt совпадает с кодом настоящего внутреннего состояния at, а в автомате класса D выходной набор wt определяет код следующего состояния at+1 (состояния перехода). Преимущество автоматов классов C и D, по сравнению с автоматами классов A и B, заключается в следующем:
- упрощается комбинационная часть автомата, поскольку отпадает необходимость в реализации комбинационной схемы CL, и
- уменьшается число используемых выходных макроячеек, так как память автомата и выходные функции реализуются на одних и тех же макроячейках ПЛИС.
Коды внутренних состояний конечного автомата могут определяться не только наборами значений выходных переменных, но также и наборами значений входных переменных [8]. Если каждый входной набор zt автомата Мили совпадает с кодом следующего состояния at+1, то имеем автомат класса E, уравнения функционирования которого имеют вид:
at+1 = zt; (5)
wt =(zt,at).
Аналогично, если каждый входной набор zt автомата Мура совпадает с кодом следующего состояния at+1, то имеем автомат класса F, поведение которого можно описать следующим образом:
at+1 = zt; (6)
wt =(at).
Особенностью структур автоматов классов E (рис. 1д) и F (рис.
1е) является отсутствие комбинационной схемы CL![]() . В автомате
класса E комбинационная схема CL
. В автомате
класса E комбинационная схема CL имеет два типа
входов: прямые (комбинационные) и буферизированные (регистровые), а в
автомате класса F - только один тип входов: буферизированные.
Необходимым условием реализации на ПЛИС автоматов классов E и F является возможность буферизации в регистрах входных сигналов. Кроме того, для построения автомата класса E входы ПЛИС должны иметь два типа связи с комбинационной частью ПЛИС: прямую и буферизированную. Буферизация входных сигналов для различных ПЛИС может осуществляться с помощью: ячеек ввода/вывода, скрытых макроячеек, выходных макроячеек и др. Для определённости любые макроячейки ПЛИС, используемые для буферизации входных сигналов, будем называть входными макроячейками ПЛИС.
Преимущество автоматов классов E и F, по сравнению с автоматами классов A и B, заключается в следующем:
- упрощается комбинационная часть автомата, поскольку отпадает необходимость в реализации комбинационной схемы CL, и
- сокращается число используемых скрытых (либо выходных, если скрытые отсутствуют) макроячеек, так как память автомата реализуется с помощью входных буферов ПЛИС.
Существенным различием между автоматами Мура классов C и F является то, что в автомате класса C выходы всегда регистровые, а в автомате класса F - комбинационные. На практике редко удаётся непосредственно реализовать автоматы классов C-F. Дело в том, что не всегда входные или выходные наборы определяют все коды внутренних состояний конечного автомата. Поэтому для построения автоматов классов C-F часто вводятся дополнительные элементы памяти путём задействования скрытых макроячеек ПЛИС.
Структурные модели конечных автоматов с регистрами на входах и выходах
Для устойчивой работы конечных автоматов входные наборы должны формироваться в заданные промежутки времени, определяемые сигналом синхронизации CLK. Если это не так, в структуры автоматов вводится входной буфер RGI, построенный на триггерах (flip-flops) или защёлках (latchs). На рис. 2 представлены структуры моделей конечных автоматов с регистрами на входах ABI, СI, DI и EI, соответствующие автоматам классов A, B, C, D и E (модель ABI является общей для автоматов классов А и В). Отметим, что автомат класса F уже имеет входной буфер и для него модель с регистром на входе совпадает с самой моделью автомата класса F.
Рисунок 2. Структуры конечных автоматов с регистрами на входах: а - объединённая модель ABBI автоматов Мили и Мура; б - модель CBI автомата класса C; в - модель DBI автомата класса D; г - модель EBI автомата класса E
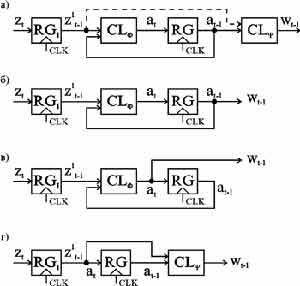
Во всех моделях ABI, СI, DI и EI регистр RGI реализуется на входных макроячейках ПЛИС. В структурах СI и DI регистр RG реализуется на выходных макроячейках ПЛИС, а в структурах ABI и EI - на скрытых, причём в структуре EI передача сигналов с выходов регистра RGI на вход регистра RG осуществляется через комбинационную часть ПЛИС.
Для некоторых устройств важно, чтобы время формирования выходных наборов определялось сигналом синхронизации CLK. С этой целью используются модели автоматов, на выходах которых устанавливается дополнительный выходной регистр RGO. На рис. 3 представлены структуры моделей конечных автоматов с регистрами на выходах ABO, DO, EO и FO, соответствующие автоматам классов A, B, D, E и F (модель ABO является общей для автоматов классов А и В). Отметим, что автомат класса C уже имеет выходной буфер в виде регистра RG, на котором реализована память автомата.
Рисунок 3. Структуры конечных автоматов с регистрами на выходах: а - объединённая модель ABO автоматов Мили и Мура; б - модель DO автомата класса D; в - модель EO автомата класса E; г - модель FO автомата класса F

В моделях ABO, DO, EO и FO регистр RGO реализуется на выходных макроячейках ПЛИС. В структурах ABO и DO регистр RG реализуется на скрытых макроячейках ПЛИС, а В структурах EO и FO - на входных макроячейках ПЛИС.
В некоторых случаях в структуры конечных автоматов приходится одновременно вводить как входные, так и выходные регистры. На рис. 4 представлены структуры моделей конечных автоматов с регистрами на входах и выходах ABIO, DIO и EIO, соответствующие автоматам классов A, B, D и E (модель ABIO является общей для автоматов классов А и В). Отметим, что для автомата класса C регистры на входе и выходе имеет модель CI, а для автомата класса F - модель FO. Во всех моделях ABIO, DIO и EIO регистр RGI реализуется на входных, RGO - на выходных, а RG - на скрытых макроячейках ПЛИС.
Рисунок 4. Структуры конечных автоматов с регистрами на входах и на выходах: а - объединённая модель ABIO автоматов Мили и Мура; б - модель DIO автомата класса D; в - модель EIO автомата класса E

Фактически все рассматриваемые модели определяются шестью классами автоматов A, B, C, D, E и F, поведение которых описывается уравнениями (3.1)–(3.6). Остальные модели (ABI, CI, DI, EI, ABO, DO, EO, FO, ABIO, DIO и EIO) представляют собой различные модификации этих шести классов путём установки регистров на входах и выходах. Поэтому для построения любой модели достаточно иметь методы синтеза конечных автоматов классов A, B, C, D, E и F. Методы синтеза на ПЛИС указанных классов конечных автоматов приводятся в [9].
Сложность реализации различных моделей конечных автоматов
Пусть конечный автомат характеризуется числом L входных переменных множества X = {x1,...,xL}, числом N выходных переменных множества Y = {y1,...,yN} и числом R разрядов кода внутренних состояний, причём R может принимать значения от intlog2M до M, где M - число внутренних состояний автомата.
На выбор модели конечного автомата при его реализации на современных ПЛИС наибольшее влияние оказывают значения следующих параметров:
- тип входа tI и выхода t0: регистровый (r) или комбинационный (c);
- число nIB входных буферов;
- число nBMC скрытых макроячеек;
- число nFF триггеров;
- число n*BMC скрытых макроячеек, когда буферизация входных сигналов осуществляется с помощью скрытых макроячеек;
- общее число nMC скрытых и внутренних макроячеек;
- суммарное число nP+BMC внешних выводов и скрытых макроячеек.
Нижние границы указанных параметров для различных моделей конечных автоматов и в зависимости от значения величин L, N и R приведены в табл. 1.
Таблица 1. Сложность реализации различных моделей конечных автоматов
| Модель | tI | tO | nIB | nBMC | nFF | n*BMC | nMC | nP+BMC |
| A | c | c | - | R | R | R | N + R | L + N + R |
| B | c | c | - | R | R | R | N + R | L + N + R |
| C | c | r | - | - | N | - | N | L + N |
| D | c | c | - | - | N | - | N | L + N |
| E | c | c | L | - | L | L | N | L + N |
| F | r | c | L | - | L | L | N | L + N |
| ABI | r | c | L | R | L + R | L + R | N + R | L + N + R |
| CI | r | r | L | - | L + R | L | N | L + N |
| DI | r | c | L | - | L + R | L | N | L + N |
| EI | r | c | L | L | 2L | 2L | L + N | 2L + N |
| ABO | c | r | - | R | N + R | R | N + R | L + N + R |
| DO | c | r | - | N | 2N | N | 2N | L + 2N |
| EO | c | r | L | - | L + N | L | N | L + N |
| FO | r | r | L | - | L + N | L | N | L + N |
| ABIO | r | r | L | R | L + N + R | L + R | N + R | L + N + R |
| DIO | r | r | L | N | L + 2N | L + N | 2N | L + 2N |
| EIO | r | r | L | L | 2L + N | 2L | L + N | 2L + N |
Общее число требуемых триггеров nFF является важным параметром при реализации конечного автомата на ПЛИС с небольшим числом триггеров, а также для ПЛИС, не имеющих входных и скрытых макроячеек (например, стандартных ПЛИС [10]). Наиболее универсальным параметром, позволяющим оценить сложность реализации различных моделей конечных автоматов и подходящим для широкого класса ПЛИС, является число nBMC требуемых скрытых макроячеек ПЛИС. Если ячейки ввода/вывода ПЛИС не имеют входных буферов (то есть буферизация входных сигналов осуществляется с помощью скрытых или выходных макроячеек ПЛИС), то вместо параметра nBMC следует использовать n*BMC, n*BMC = nBMC + nIB. При реализации конечного автомата на сложных ПЛИС [11], когда размер входного буфера не критичен, поскольку буферизация входных сигналов осуществляется с помощью ячеек ввода/вывода, стоимость реализации модели можно оценить по общему числу nMC скрытых и выходных макроячеек, nMC = nBMC + N. Наоборот, при реализации конечного автомата на стандартных ПЛИС, когда наблюдается дефицит числа внешних выводов и скрытых макроячеек, в качестве оценки сложности реализации может выступать параметр nP+BMC, nP+BMC = nBMC + L + N.
Анализ сложности реализации по универсальному параметру nBMC показывает, что среди моделей конечных автоматов с комбинационными входами и комбинационными выходами наилучшими являются модели D и E; с комбинационными входами и регистровыми выходами - C и EO; с регистровыми входами и комбинационными выходами - F и DI; с регистровыми входами и регистровыми выходами - CI и FO.
Временной анализ основных моделей конечных автоматов
При временном анализе работы ПЛИС наиболее важными параметрами являются следующие:
- tCO - время установки регистровых выходов ПЛИС;
- tPD - время задержки на комбинационной части ПЛИС (время установки комбинационных выходов);
- tS - время удержания;
- tH - время задержки данных на входах триггеров.
Длительность минимального периода времени смены состояний автомата tP определяется величиной
tP = tS + tCO, (7)
а максимальная частота функционирования конечного автомата fmax определяется из выражения:
fmax = 1/tP. (8)
Временные диаграммы функционирования основных моделей конечных автоматов и моделей с регистрами на выходах показаны на рис. 5. Промежуток времени, в течение которого автомат находится в определённом состоянии, будем называть тактом автомата или просто тактом. Начало каждого такта на рис. 5 определяется установкой стабильного внутреннего состояния автомата. В каждом такте сигналы цепей обратных связей, определяющие код внутреннего состояния автомата, и входные сигналы должны быть стабильными на протяжении времени tS до прихода переднего фронта импульса синхронизации CLK и должны оставаться стабильными время tH после его прихода. Код следующего состояния появится на выходах триггеров через время tCO после прихода синхроимпульса, причём этому моменту будет предшествовать короткий промежуток времени нестабильности регистровых выходов.
Рисунок 5. Временные диаграммы функционирования основных структур конечных автоматов и моделей с регистрами на выходах

Выходные сигналы автоматов Мили и Мура классов A и B в пределах каждого такта формируются одновременно, однако выходные сигналы автомата Мура класса В остаются стабильными больший промежуток времени, чем выходные сигналы автомата Мили класса А, поскольку в структуре В выходные сигналы зависят только от смены состояний, а в структуре А ещё и от изменения входных сигналов.
В структуре автомата класса С выходные сигналы изменяются одновременно
со сменой состояния, то есть на время tPD раньше, чем в структурах
автоматов классов А и В, поскольку отсутствует задержка на комбинационной
схеме CL. Поэтому автомат класса С обладает наивысшим
быстродействием в смысле момента формирования выходных сигналов в пределах
одного такта. Последнее справедливо лишь в случае, когда в начальном
состоянии автомата класса C формируется нулевой выходной набор, в
противном случае, автомат класса C функционирует с запаздыванием на один
такт [9].
Выходные сигналы автоматов классов D и E формируются в те же моменты времени, что и в структуре А: через время tPD после установки состояния - и остаются стабильными на протяжении времени, равном стабильности входных сигналов. Выходные сигналы автомата класса F формируются так же, как в автомате Мура класса B.
В структурах автоматов ABO, DO, EO и FO с регистрами на выходах выходные сигналы формируются так же, как в автомате класса С, но с задержкой на один такт.
Временные диаграммы функционирования автоматов структур моделей ABI, CI, DI и EI с регистрами на входах и структур моделей ABIO, DIO и EIO с регистрами как на входах, так и на выходах, показаны на рис. 6. Для устойчивой работы входных регистров RGI входные сигналы zt должны оставаться стабильными время tS до прихода синхроимпульса и время th после синхроимпульса. Входные сигналы набора zt¹, снимаемые с выходов регистров RGI, будут стабильными через время tCO после синхроимпульса и останутся стабильными до начала следующего такта. Смене значений сигналов zt¹ предшествует короткий промежуток времени нестабильности, объясняемый срабатыванием регистра RGI.
Рисунок 6. Временные диаграммы функционирования структур конечных автоматов с регистрами на входах и регистрами на входах и выходах

Недостатком структур ABI, CI, DI и EI с регистрами на входах является то, что автоматы будут функционировать с запаздыванием на один такт. Кроме того, не достигнута главная цель: возможность изменения входных сигналов в произвольные моменты времени. Дело в том, что для корректной работы регистров RGI сигналы zt должны изменяться так же, как в рассмотренных ранее структурах: в строго определённый период времени в пределах каждого такта.
Структурам ABIO, DIO и EIO (рис. 4) с регистрами одновременно на входах и выходах присущи все недостатки структур с регистрами на выходах и регистрами на входах. Регистры на входах вызывают запаздывание функционирования автомата на один такт, а регистры на выходах являются причиной задержки ещё на один такт формируемых выходных сигналов. Таким образом, в структурах ABIO, DIO и EIO выходные сигналы формируются с запаздыванием на два такта.
Модели конечных автоматов с защелками на входах
Для буферизации входных сигналов, которые могут изменяться в произвольные моменты времени, применяются не триггеры (flip-flops), а защёлки (latches). При этом используются раздельные сигналы синхронизации: CLKI - для входных защёлок и CLK - для остальных частей схемы. В ПЛИС защёлки пропускают входные сигналы без изменений при высоком значении сигнала синхронизации CLKI и сохраняют последние значения входных сигналов при низком значении CLKI. Если время tWL низкого значения сигнала синхронизации CLKI принять равным tS + tH, а время tWH высокого значения сигнала синхронизации CLKI принять равным tCO – tH, то получим структуру автомата с защёлками на входах, работающую на максимальной частоте и допускающую изменение входных сигналов в произвольные моменты времени (рис. 7).
Рисунок 7. Структура автомата с защёлками на входах (а) и временная диаграмма его работы (б)

Модели конечных автоматов с защёлками на входах ABI’, CI’, DI’, EI’, ABIO’, DIO’ и EIO’ функционируют аналогично структурам ABI, CI, DI, EI, ABIO, DIO и EIO с триггерами на входах, но на один такт быстрее.
Использование моделей конечных автоматов в цифровых системах
Структуру многоуровневой цифровой системы S, состоящей из K уровней,
можно представить в виде совокупности последовательно соединённых
подсистем S1,...,SK (рис.
8а). Здесь обрабатываемые данные DI поступают на входы
первой подсистемы S1, а выходные данные DO
формируются на выходах последней подсистемы SK; выходы каждой
подсистемы Sk (за исключением последней) подсоединены ко входам
следующей подсистемы Sk+1, ![]() .
.
Рисунок 8. Общая структура многоуровневой цифровой системы (а) и временные диаграммы сигналов синхронизации (б)
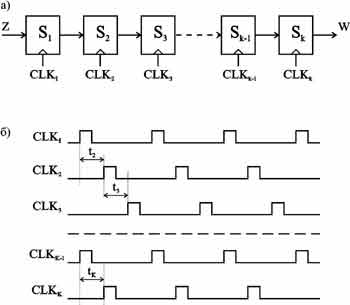
Пусть каждая подсистема Sk тактируется отдельным сигналом
синхронизации CLKk, ![]() . Начало каждого такта
следующего логического уровня k,
. Начало каждого такта
следующего логического уровня k, ![]() , может начинаться не
раньше установки стабильного состояния выходов предыдущего уровня k–1.
Поэтому каждый сигнал CLKk должен иметь фазовый сдвиг на время
tk,
, может начинаться не
раньше установки стабильного состояния выходов предыдущего уровня k–1.
Поэтому каждый сигнал CLKk должен иметь фазовый сдвиг на время
tk, ![]() , от тактов синхронизации предыдущего уровня (рис.
8б). Отметим, что если быстродействие всех подсистем
S1,...,SK-1 одно и то же, то величины
t2,...,tK могут иметь одинаковые значения.
, от тактов синхронизации предыдущего уровня (рис.
8б). Отметим, что если быстродействие всех подсистем
S1,...,SK-1 одно и то же, то величины
t2,...,tK могут иметь одинаковые значения.
При выборе модели конечного автомата для использования в цифровой системе важнейшими временными параметрами являются следующие:
- TPOS - время задержки формирования выходных сигналов от начала такта, измеряемое в периодах;
- TOS - время задержки формирования выходных сигналов в пределах такта;
- TSD - время стабильного значения выходов в пределах такта.
На основании этих параметров можно определить полное время задержки выходных сигналов от начала такта Q:
Q = TPOS + TOS. (9)
Значения параметров TPOS, TOS, TSD и Q для рассматриваемых моделей конечных автоматов приведены в табл. 2.
Таблица 2. Временные параметры моделей конечных автоматов
| № | Модель | TPOS | TOS | TSD | Q |
| 1 | A | 0 | tPD | tS + tH | tPD |
| 2 | B | 0 | tPD | tP | tPD |
| 3 | C | 0 | 0 | tP | 0 |
| 4 | D | 0 | tPD | tS + tH | tPD |
| 5 | E | O | tPD | tS + tH | tPD |
| 6 | F | 0 | tPD | tP | tPD |
| 7 | ABI | tP | tPD | tP | tP + tPD |
| 8 | CI | tP | 0 | tP | tP |
| 9 | DI | tP | tPD | tP | tP + tPD |
| 10 | EI | tP | tPD | tP | tP + tPD |
| 11 | ABO | tP | 0 | tP | tP |
| 12 | DO | tP | 0 | tP | tP |
| 13 | EO | tP | 0 | tP | tP |
| 14 | FO | tP | 0 | tP | tP |
| 15 | ABIO | 2tP | 0 | tP | 2tP |
| 16 | DIO | 2tP | 0 | tP | 2tP |
| 17 | EIO | 2tP | 0 | tP | 2tP |
| 18 | AB'I | 0 | tPD | tS + tH | tPD |
| 19 | C'I | 0 | 0 | tP | 0 |
| 20 | D'I | 0 | tPD | tS + tH | tPD |
| 21 | E'I | 0 | tPD | tS + tH | tPD |
| 22 | AB'IO | tP | 0 | tP | tP |
| 23 | D'IO | tP | 0 | tP | tP |
| 24 | E'IO | tP | 0 | tP | tP |
При выборе модели конечного автомата удобно пользоваться параметрами Q и TSD. В зависимости от значений этих параметров, все модели конечных автоматов можно разделить на шесть групп M1,...,M6 (табл. 3).
Таблица 3. Группы моделей в зависимости, от временных параметровв
| Группа | Q | TSD | Модели |
| M1 | 0 | tP | C, C'I |
| M2 | tPD | tP | B, F |
| M3 | tPD | tS + tH | A, D, E, AB'I, D'I, E'I |
| M4 | tP | tP | CI, ABO, DO, EO, FO, AB'IO, D'IO, E'IO |
| M5 | tP + tPD | tP | ABI, DI, E |
| M6 | 2tP | tP | ABIO, DIO, EIO |
Использование моделей конечных автоматов в последовательных цифровых системах
Рассмотрим два класса многоуровневых последовательных цифровых систем: с раздельной и общей синхронизацией.
В цифровой системе с раздельной синхрониза-цией каждая подсистема
Sk (рис.
8) тактируется отдельным синхросигналом CLKk, ![]() . Поскольку
начало каждого такта следующего уровня должно начинаться не ранее
установки стабильного состояния выходов предыдущего уровня, то
быстродействие (время прохождения обрабатываемых данных со входа на выход
системы) последовательной системы S определяется следующим образом:
. Поскольку
начало каждого такта следующего уровня должно начинаться не ранее
установки стабильного состояния выходов предыдущего уровня, то
быстродействие (время прохождения обрабатываемых данных со входа на выход
системы) последовательной системы S определяется следующим образом:
(10)
где Qk - максимальное значение параметра Q для моделей конечных автоматов, используемых на уровне.
В цифровой системе с общей синхронизацией все подсистемы S1,...,SK тактируются одним и тем же синхросигналом CLK. Для определения быстродействия такой системы будем считать, что на каждом уровне используются модели, содержащие только один регистр (то есть модели первых трёх групп). Если модель конечного автомата некоторого уровня , содержит несколько регистров, то её синхронизация должна осуществляться собственным внутренним синхросигналом, согласованным с сигналом CLK. Период синхросигнала CLK в цифровой системе с общей синхронизацией определяется по самой медленной модели. Поэтому быстродействие последовательной цифровой системы в случае общей синхронизации выражается следующим образом:
P2 = K·(Qmax + tP), (11)
где Qmax - максимальное значение параметра Q из всех используемых в цифровой системе моделей.
Из (3.11) и (3.12), а также табл. 3 следует, что быстродействие последовательных цифровых систем ухудшается с ростом номера группы моделей конечных автоматов.
Использование моделей конечных автоматов в конвейерных цифровых системах
Отметим некоторые необходимые условия для возможности построения конвейерной цифровой системы. На всех уровнях должны применяться модели с одинаковыми временными параметрами, то есть принадлежать одной из групп M1,...,M6 (табл. 3). Цифровая система S должна иметь общую синхронизацию, то есть все подсистемы тактируются одним и тем же синхросигналом CLK. Если значение параметра TOS для используемых моделей равно нулю, то период tC синхросигнала CLK принимается равным tP; если TOS = tPD, то значение tC принимается равным tP + tPD. На основании вышеизложенного быстродействие конвейерной многоуровневой цифровой системы можно выразить следующим образом:
G = (K – 1)·tC + Q. (12)
Значения быстродействия G конвейерной многоуровневой цифровой системы для различных групп моделей приведены в табл. 4. На рис. 9 показаны графики быстродействия G1,...,G6 различных групп моделей в зависимости от значения числа K уровней цифровой системы.
Таблица 4. Быстродействие моделей a конвейерных цифровых системах
| Группа | Q | tC | G |
| M1 | 0 | tP | G1 = (k – 1)·tP |
| M2 | tPD | tP + tPD | G2 = (k – 1)·(tP + tPD) + tPD |
| M3 | tPD | tP + tPD | G3 = (k – 1)·(tP + tPD) + tPD |
| M4 | tP | tP | G4 = k·tP |
| M5 | tP + tPD | tP + tPD | G5 = k·(tP + tPD) |
| M6 | 2tP | tP | G6 = k·tP + tP |
Рисунок 9. Быстродействие различных моделей конечных автоматов в многоуровневых конвейерных цифровых системах
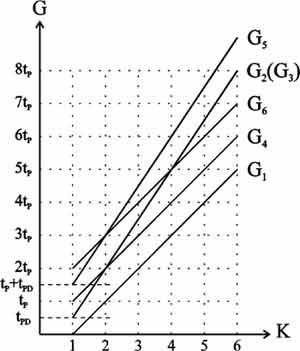
Из анализа графиков на рис. 9 можно определить следующие неравенства:
~G1 < G4 < G6;
G1 < G2(G3) < G5; (13)
G4 < G5.
Таким образом, самой быстродействующей группой моделей конечных автоматов является группа M1. Модели групп M2(M3) и M5 могут иметь преимущество, по сравнению с моделями M4 и M6, соответственно, только для малых значений K. С ростом числа уровней K преимущество моделей M4 и M6 становится очевидным.
Совмещенные модели конечных автоматов
При синтезе конечных автоматов, несмотря на свою эффективность, модели автоматов классов C, D, E и F редко используются "в чистом виде", а часто вместе с моделями A и B. Это объясняется тем, что не всегда выполняются необходимые условия возможности построения автоматов классов C-F. Поэтому на практике применяется совмещение различных моделей при построении одного и того же автомата [9].
Главным критерием возможности совмещения в одной структуре различных моделей конечных автоматов является согласование временных параметров формируемых выходных сигналов: TPOS, TOS и TSD. Модели, в которых эти параметры не совпадают (особенно TPOS), нельзя объединять в одной структуре конечного автомата, так как это ведёт к непредсказуемости значений формируемых выходных сигналов.
На рис. 10 показаны четыре возможные структуры совмещённых моделей. Первая структура соответствует автомату Мура класса C; вторая - автоматам Мура классов B и F; третья - автоматам Мили классов A, D и E; четвёртая - совмещённой модели всех классов автоматов (A-F) с регистрами на выходах. Отметим, что установка дополнительных регистров на выходах автомата позволяет совмещать любые модели автоматов, поскольку временные параметры выходных сигналов для всех моделей уравниваются. Все представленные на рис. 10 структуры могут модифицироваться путём установки на входах регистров и защёлок, а структуры на рис. 10б и 10в - ещё и регистров на выходах.
Рисунок 10. Структуры возможных совмещённых моделей конечных автоматов: а - автомата Мура класса C; б - автоматов Мура классов B и F; в - автоматов Мили классов A, D и E; г - общей совмещённой модели автоматов с регистрами на выходах
В общем случае, действительно совмещёнными моделями конечных автоматов являются модели ADE, AD, AE и BF (сочетание букв в обозначении совмещённой модели указывает на классы конечных автоматов, входящих в совмещённую модель).
Выбор моделей конечных автоматов на ПЛИС
В разделах "Классы конечных автоматов", "Структурные модели конечных автоматов с регистрами на входах и выходах" и "Модели конечных автоматов с защелками на входах" были определены 24 базовые модели конечных автоматов, которые могут быть реализованы на ПЛИС. Затем в разделе "Использование моделей конечных автоматов в цифровых системах" были введены совмещённые модели ADE, AD, AE и BF. Поскольку на входах совмещённых моделей также могут устанавливаться регистры или защёлки, а на выходах - регистры, общее число моделей конечных автоматов, которые допускают реализацию на ПЛИС, равняется 50. Поэтому выбор подходящих моделей для реализации на ПЛИС частей цифровой системы, представленных конечными автоматами, является не тривиальной задачей.
При обозначении моделей приняты следующие правила: нижний индекс I указывает на наличие дополнительного входного буфера, построенного на триггерах; апостроф (‘) вместе с нижним индексом I обозначает, что дополнительный входной буфер построен на защёлках; нижний индекс O указывает на наличие дополнительного выходного буфера на триггерах.
При выборе моделей конечных автоматов необходимо учитывать следующие факторы:
- довлетворение системным требованиям;
- архитектурные возможности ПЛИС для реализации моделей;
- временные параметры, влияющие на производительность цифровой системы;
- стоимость реализации моделей на ПЛИС.
Среди системных требований, предъявляемых к синтезируемым конечным автоматам, в первую очередь необходимо учитывать тип входов и выходов. Входы конечных автоматов, реализуемых на ПЛИС, могут быть комбинационными или буферизированными, причём в качестве буферов могут использоваться триггеры или защёлки; выходы могут быть комбинационными или регистровыми. Особенно внимательно следует относиться к использованию моделей с комбинационными входами и выходами, когда выходные функции конечного автомата непосредственно зависят от входных переменных. В таких моделях любые изменения на входах будут вызывать изменения значений выходов. Классификация моделей конечных автоматов по типам входов и выходов приведена в табл. 5.
Таблица 5. Группы моделей кон. автоматов, в зависимости от типа входов и выходов
| Gi | Типы входов и выходов | Модели |
| G1 | Комбинационный вход, комбинационный выход | A, B, D, E, ADE, AD, AE, BF |
| G2 | Регистровый вход, комбинационный выход | F, ABI, DI, EI, ADEI, ADI, AEI, BFI |
| G3 | Комбинационный вход, регистровый выход | C, ABO, DO, EO, ADEO, ADO, AEO, BFO |
| G4 | Регистровый вход, регистровый выход | CI, FO, ABIO, DIO, EIO, ADEIO, ADIO, AEIO, BFIO |
| G5 | Защелки на входах, комбинационный выход | AB'I, D'I, E'I, F'I, ADE'I, AD'I, AE'I, BF'I |
| G6 | Защелки на входах, регистровый выход | C'I, AB'IO, D'IO, E'IO, F'IO, ADE'IO, AD'IO, AE'IO, BF'IO |
| G7 | Непосредственная связь выходов со входами | A, D, E, ADE, AD, AE, BF |
Следующим важным моментом при выборе моделей является наличие архитектурных свойств используемой ПЛИС, достаточных для реализации выбранных моделей конечных автоматов. Для рассматриваемых моделей наиболее важными архитектурными свойствами ПЛИС, определяющими возможность реализации соответствующих моделей, является наличие триггера в цепях обратных связей (RGF); наличие входного буфера (RGI), по умолчанию построенного на триггерах; возможность построения входного буфера на защёлках (RGI’); наличие двух связей входного буфера (прямой и буферизированной) с комбинационной частью ПЛИС (RGI2). В табл. 6 приводятся различные возможные сочетания указанных архитектурных свойств ПЛИС и реализуемые при этом модели. Отметим, что модели A, B, C и ABO предъявляют минимальные требования к архитектурным свойствам ПЛИС.
Таблица 6. Возможность реализации моделей конечных автоматов, в зависимости от свойств PLD.
| Gj | Свойства PLD | Модели | |||
| RGF | RGI | RG'I | RGI2 | ||
| G1 | D, AD, DO, ADO | ||||
| G2 | F, BF, ABI, CI, BFI, FO, BFO, ABIO, BFIO | ||||
| G3 | DI, ADI, DIO, ADIO | ||||
| G4 | E, AE, EI, AEI, EO, AEO, EIO, AEIO, | ||||
| G5 | AB'I, C'I, F'I, BF'I, AB'IO, F'IO, BF'IO | ||||
| G6 | ADE, ADEI, ADEO, ADEIO | ||||
| G7 | D'I, AD'I, D'IO, AD'IO | ||||
| G8 | E'I, AE'I, E'IO, AE'IO | ||||
| G9 | ADE'I, ADE'IO | ||||
| G10 | A, B, C, ABO | ||||
Как было показано в разделе "Структурные модели конечных автоматов с регистрами на входах и выходах", временные параметры моделей конечных автоматов определяют максимальное быстродействие всей цифровой системы. Важнейшими временными параметрами моделей конечных автоматов являются TPOS, TOS, TSD и Q, определённые в разделе "Использование моделей конечных автоматов в цифровых системах". Временные параметры для различных групп моделей приведены в табл. 7, здесь tPD, tS, tH и tP - временные параметры ПЛИС, определённые в разделе "Временной анализ основных моделей конечных автоматов"; в скобках указаны модели автомата класса C, когда в начальном состоянии формируется ненулевой выходной набор.
Таблица 7. Группы моделей кон. автоматов, в зависимости от временных параметров
| TPOS | TOS | TSD | Q | Модели |
| 0 | tPD | tS + tH | tPD | C, C'I |
| 0 | tPD | tP | tPD | B, F, BF, F'I, BF'I |
| 0 | 0 | tP | 0 | A, D, E, ADE, AD, AE, AB'I, D'I, E'I, ADE'I, AD'I, AE'I |
| tP | tPD | tP | tP + tPD | CI, ABO, DO, EO, FO, ADEO, ADO, AEO, BFO, AB'IO, D'IO, E'IO, F'IO, ADE'IO, AD'IO, AE'IO, BF'IO (C) |
| tP | 0 | tP | tP | ABI, DI, EI, ADEI, ADI, AEI, BFI |
| 2tP | 0 | tP | 2tP | ABIO, DIO, EIO, ADEIO, ADIO, AEIO, BFIO (CI) |
Целью выбора моделей конечных автоматов, в зависимости от временных параметров, является обеспечение максимального быстродействия цифровой системы. При этом следует учитывать тип цифровой системы: последовательная или конвейерная. В случае последовательной цифровой системы следует также различать системы с раздельной и общей синхронизацией.
Для выбора минимальной по стоимости реализации на ПЛИС модели конечного автомата прежде всего необходимо определить критерий качества стоимости реализации, который определяется архитектурными свойствами используемого ПЛИС. Оценка стоимости реализации групп моделей конечных автоматов по минимальному числу nBMC скрытых макроячеек, требуемых для реализации, приведена в табл. 8. После определения критерия качества на основании параметров конкретного автомата (L, N и R) можно приблизительно оценить стоимость реализации каждой модели.
Таблица 8. Группы моделей, в зависимости от минимальной оценки стоимости реализации на PLD
| Gm | nBMC | Модели |
| G1 | 0 | С, D, E, F, ADE, AD, AE, BF, CI, DI, ADI, EO, FO, AEO, BFO, C'I, D'I, AD'I |
| G2 | R | A, B, ABI, ABO, ABIO, AB'I, AB'IO |
| G3 | N | DO, ADEO, ADO, DIO, ADIO, D'IO, AD'IO |
| G4 | L | EI, ADEI, AEI, BFI, EIO, AEIO, BFIO, E'I, F'I, ADE'I, AE'I, BF'I, E'IO, F'IO, AE'IO, BF'IO |
| G5 | L + N | ADEIO, ADE'IO |
Алгоритм (выбора моделей для реализации на ПЛИС конечных автоматов цифровой системы):
- Для некоторого автомата Af из всего множества M моделей
конечных автоматов в соответствии с табл.
5 выбирается подмножество M*, удовлетворяющее типам входов и выходов
конечного автомата. Полагается: M* := UiGi, где
Gi - группа моделей конечных автоматов, определяемая по табл.
5, которая удовлетворяет требованиям к типам входов и выходов
конечного автомата,
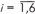 .
.
- Если конечный автомат Af имеет комбинационные входы и выходы и имеется опасность изменения значений входных переменных в произвольные моменты времени, то полагается M* := M*\G7, где группа моделей G7 определяется из табл. 5.
- На основании архитектурных свойств используемого ПЛИС определяются
значения параметров RGF, RGI, RGI’ и
RGI2. Согласно табл.
6, определяется группа моделей , которые могут быть реализованы на
заданном ПЛИС. Полагается M* := M*
 (Gj
(Gj  G10).
G10).
- На основании типа цифровой системы (последовательная или
конвейерная), способа синхронизации для по-следовательной системы (общая
или раздельная) и временных параметров моделей в табл.
7 определяется группа моделей
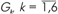 , обеспечивающая
максимальное быстродействие цифровой системы. Полагается M* := M*
, обеспечивающая
максимальное быстродействие цифровой системы. Полагается M* := M*  Gk.
Gk.
- На основании архитектурных свойств ПЛИС определяется критерий оценки стоимости реализации моделей конечного автомата.
- На основании выбранного в пункте "Временной анализ основных моделей
конечных автоматов" критерия оценки стоимости реализации на ПЛИС и
параметров конечного автомата Af по табл.
8 определяется группа
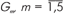 , моделей с
минимальной стоимостью реализации. Полагается M* := M* З Gm.
, моделей с
минимальной стоимостью реализации. Полагается M* := M* З Gm.
- Конец.
Отметим, что этот алгоритм может применяться для выбора моделей к отдельному конечному автомату, к некоторому подмножеству конечных автоматов, например, принадлежащих одному уровню цифровой системы, а также ко всем конечным автоматам цифровой системы.
Пример. Пусть ПЛИС допускает конфигурацию выходных макроячеек с триггером в цепи обратной связи, то есть обладает свойством RGF. Проектируется многоуровневая конвейерная система, на вход которой данные поступают синхронно. Необходимо выбрать модели конечных автоматов для построения цифровой системы максимального быстродействия с синхронной выдачей выходных данных.
В данном примере с помощью алгоритма определяются подходящие модели для
всех автоматов цифровой системы. Поскольку данные на вход цифровой системы
поступают синхронно, нет необходимости буферизировать входные данные.
Однако поскольку система является конвейерной, выходы каждого уровня, в
том числе и последнего, удовлетворяющего условию синхронизации входов,
должны быть синхронизированы. Поэтому в пункте 1 алгоритма выбираем группу
моделей G3 с комбинационными входами и регистровыми выходами,
полагается M* = {C, ABO, DO, EO,
ADEO, ADO, AEO, BFO}.
Выполнение пункта 2 не изменяет содержимое множества M*. Поскольку ПЛИС
обладает только одним свойством RGF, в результате выполнения
пункта 3 множество M* пересекается с группами G1 и
G10 из табл.
6, в результате получим M* = {C, ABO, DO,
ADO}. Для конвейерных цифровых систем важнейшими временными
параметрами являются Q и TSD. Поскольку неизвестно, какие наборы
формируются в начальном состоянии автоматов Мура, группа G1
исключается из рассмотрения, а модель C принимается из группы
G4. Все элементы множества M* принадлежит группе моделей
G4, поэтому выполнение пункта 4 алгоритма не изменяет
содержимое множества M*. Поскольку отсутствует какая-либо информация об
архитектуре ПЛИС, в качестве критерия стоимости реализации моделей
принимается минимальное число nBMC скрытых макроячеек. В
результате выполнения пункта 5 в табл.
8 выбирается группа моделей G1, получаем M* := M* ![]() G1 = {C}. Таким образом, для реализации конечных автоматов
конвейерной цифровой системы на ПЛИС с указанными свойствами наиболее
подходящей является модель автоматов Мура класса C.
G1 = {C}. Таким образом, для реализации конечных автоматов
конвейерной цифровой системы на ПЛИС с указанными свойствами наиболее
подходящей является модель автоматов Мура класса C.
Литература