Параллельные алгоритмы обработки данных. Умножение матриц

Автор: Миронов А.А., Карпов А.Н.

Источник: http://www.viva64.com/content/articles/parallel-programming/?f=Parallel_processing_rus.html

Задача умножения матриц является базовой макрооперацией для многих задач линейной алгебры. Поэтому эффективный параллельный алгоритм умножения матриц позволяет значительно увеличить размерность подобных задач без увеличения времени их решения. Пусть даны две матрицы, A_N,M и B_N,M , произведение которых необходимо вычислить. Элементы результирующей матрицы С=AxB определяются по формуле

Оценим время выполнения последовательного алгоритма. Пусть T_m — время, затрачиваемое на умножение двух чисел, T_a — время сложения двух чисел. Время, затрачиваемое на вычисление одного элемента результирующей матрицы 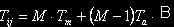В результирующей матрице содержится MxN элементов, поэтому общее время выполнения умножения матриц равно

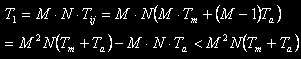
Обозначим

Отсюда следует, что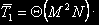

Рассмотрим параллельный алгоритм умножения матриц и оценим время его работы.

Пусть имеется K процессоров, причём, M*N=X*K, где X — целое. Распараллелим вычисления так, чтобы каждый процессор вычислял M*N/K элементов результирующей матрицы. Тогда суммарное время выполнения можно оценить следующим образом:

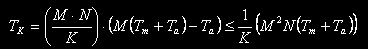
Обозначим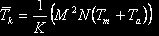

Сравнивая и 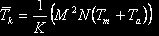, получим: 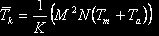/=K

Имеем, что время, затрачиваемое на умножение матриц с помощью параллельного алгоритма, в K раз меньше, чем при использовании последовательного.

Рассмотрим один из способов распараллеливания алгоритма. Пронумеруем элементы результирующей матрицы по следующему правилу (нумерация элементов, а также строк и столбцов в данном случае ведётся с нуля):

n_ij=i*N+j

Вычисления распределим так, чтобы первый процессор вычислял первые M*N/K элементов результирующей матрицы, второй — следующие M*N/K и т.д. Таким образом, конечная и левая исходная матрица получаются распределёнными горизонтальными полосами, а правая исходная матрица — вертикальными полосами.

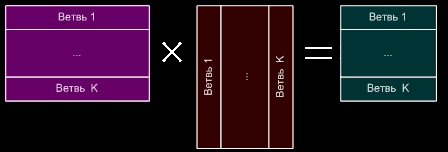
Рис.1. Схема распределения работ при параллельном умножении матриц.

Рассмотрим случай, когда K>M*N (количество процессоров больше, чем элементов в результирующей матрице). Незадействованные M*N-K процессоров можно использовать для ускорения вычисления отдельных элементов результирующей матрицы. При этом следует использовать способ распараллеливания, подобный использованному при вычислении скалярного произведения векторов.

// Параллельное умножение матриц
#include "windows.h"
#include "process.h"
#include "stdio.h"

#define M 3
#define N 4
#define NumberOfProcessors 3

int A[M][N];
int B[N][M];
int C[M][M];

void InititalizeMatices()
{
  unsigned i, j, n;

  printf("\nMatrix A:\n");
  for (i = 0, n = 1; i < M; i++)
  {
    for (j = 0; j < N; j++, n++)
    {
      A[i][j] = n;
      printf("%4d ", n);
    }
    printf("\n");
  }

  printf("\nMatrix B:\n");
  for (i = 0, n = 1; i < N; i++)
  {
    for (j = 0; j < M; j++, n++)
    {
      B[i][j] = n;
      printf("%4d ", n);
    }
    printf("\n");
  }
}

unsigned __stdcall ThreadFunction(void *pData)
{
  unsigned Branch = (unsigned)pData;
  unsigned Start = M / NumberOfProcessors * Branch;
  unsigned End = M / NumberOfProcessors * (Branch + 1);
  for (unsigned i = Start; i < End; i++)
    for (unsigned j = 0; j < M; j++)
    {
      int Value = A[i][0] * B[0][j];
      for (unsigned k = 1; k < N; k++)
        Value += A[i][k] * B[k][j];
      C[i][j] = Value;
    }
  return 0;
}


int main(int argc, char* argv[])
{
  UNREFERENCED_PARAMETER(argc);
  UNREFERENCED_PARAMETER(argv);
  assert(M % NumberOfProcessors == 0);

  InititalizeMatices();

  HANDLE hThreads[NumberOfProcessors];
  unsigned i, j, n, tid;
  for (i = 0; i < NumberOfProcessors; i++)
    hThreads[i] = (HANDLE)_beginthreadex(NULL, 0, 
      ThreadFunction, (void *)i, 0, &tid);

  WaitForMultipleObjects(NumberOfProcessors, hThreads, TRUE,
                         INFINITE);

  for (i = 0; i < NumberOfProcessors; i++)
    CloseHandle(hThreads[i]);

  printf("\nMatrix C = A * B:\n");
  for (i = 0, n = 1; i < M; i++)
  {
    for (j = 0; j < M; j++, n++)
      printf("%4d ", C[i][j]);
    printf("\n");
  }

  return 0;
}